Основные характеристики функции
Виды функций
 Если функция представлена в виде
Если функция представлена в виде  , где переменная
, где переменная 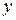 выражается через переменную
выражается через переменную 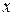 , то функция задана в явном виде (явная функция).
, то функция задана в явном виде (явная функция).
Пример 1.1. Дана функция 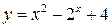 . Найти значения при
. Найти значения при 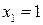 ,
, 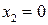 ,
, 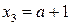 .
.
Решение. Находим значения функции, подставляя вместо 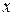 конкретное значение:
конкретное значение:
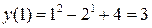 ;
;
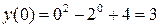 ;
;
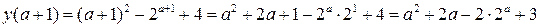 .
.
,
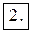 Если функция задана в виде уравнения
Если функция задана в виде уравнения 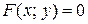 , где переменная
, где переменная 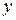 не выражена через переменную
не выражена через переменную 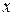 , то функция задана неявно.
, то функция задана неявно.
Пример 1.2. Дана функция в виде уравнения 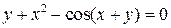 . Найти значение в точке
. Найти значение в точке 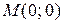 .
.
Решение. Находим значение функции, подставляя 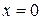 и
и 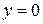 :
:
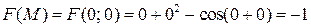 .
.
,
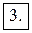 Если зависимость между аргументом
Если зависимость между аргументом 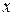 и функцией
и функцией 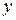 (на плоскости
(на плоскости 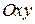 ) задана в виде уравнений
) задана в виде уравнений
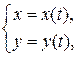
где 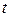 − вспомогательная переменная, называемая параметром, то функция называется задана параметрически.
− вспомогательная переменная, называемая параметром, то функция называется задана параметрически.
В 3-х-мерном пространстве функция, заданная параметрически имеет следующий вид:
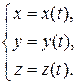
Кстати, в определенных случаях – это на плоскости 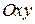 , − можно от параметрически заданной функции перейти к аналитическому заданию.
, − можно от параметрически заданной функции перейти к аналитическому заданию.
Пример 1.3. Дана функция 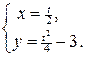 Найти значение при
Найти значение при 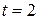 . Записать функцию аналитически. [Построить график.]
. Записать функцию аналитически. [Построить график.]
Решение. Находим значение функции при 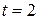 :
: 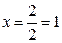 ;
; 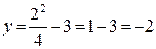 .
.
Итак, получаем точку 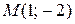 .
.
Из первого уравнения выражаем 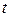 через
через 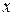 :
: 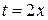 . Подставляем во второе уравнение. Получаем
. Подставляем во второе уравнение. Получаем
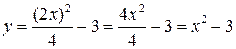 .
.
Итак, функция примет вид: 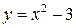 . Графиком этой функции является парабола.
. Графиком этой функции является парабола.
,
 Рассмотрим радиус-вектор некоторой точки
Рассмотрим радиус-вектор некоторой точки 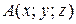 в пространстве
в пространстве 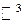 . Радиус-вектор
. Радиус-вектор 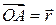 можно записать в виде
можно записать в виде
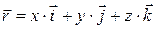 .
.
Если проекции вектора 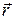 есть функции некоторого параметра
есть функции некоторого параметра 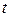 , т.е.
, т.е. 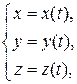 то функция задана векторным уравнением или вектор-функцией:
то функция задана векторным уравнением или вектор-функцией:
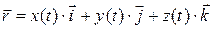 .
.
Например, 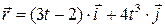 в
в 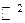 .
.
От вектор-функции можно перейти к функции, заданной параметрически, и наоборот. Если в векторное уравнение подставить определенное значение параметра 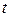 , то получим алгебраический вектор.
, то получим алгебраический вектор.
 Особый класс составляют функции, область определения которых является множество натуральных чисел, т.е.
Особый класс составляют функции, область определения которых является множество натуральных чисел, т.е. 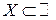 .
.
Если каждому натуральному числу 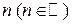 поставлено в соответствие число
поставлено в соответствие число 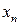 , то говорят, что задана числовая последовательность (множество занумерованных чисел)
, то говорят, что задана числовая последовательность (множество занумерованных чисел) 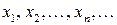 , которая обозначается
, которая обозначается 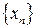 , где
, где 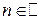 .
.
Числа 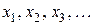 называются элементами или членами последовательности, а число
называются элементами или членами последовательности, а число 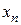 − общим или n-ымчленом данной последовательности. Иногда последовательность
− общим или n-ымчленом данной последовательности. Иногда последовательность 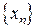 задают формулой общего члена последовательности:
задают формулой общего члена последовательности: 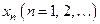 .
.
Например,
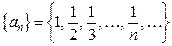 , где
, где 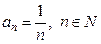 ;
;
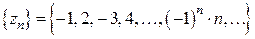 , где
, где 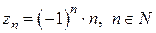 ;
;
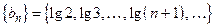 , где
, где 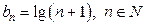 .
.
Геометрически последовательность изображается на числовой прямой в виде множества точек, координаты которых равны соответствующим элементам последовательности.
Определение 1.2. Графиком функции  называется множество всех точек плоскости Oxy, для каждой из которых x является значением аргумента, а y – соответствующим значением функции.
называется множество всех точек плоскости Oxy, для каждой из которых x является значением аргумента, а y – соответствующим значением функции.
Чтобы задать функцию  , необходимо указать правило, позволяющее, зная x, находить соответствующее значение y. Наиболее часто встречаются три способа задания функции: аналитический, табличный, графический.
, необходимо указать правило, позволяющее, зная x, находить соответствующее значение y. Наиболее часто встречаются три способа задания функции: аналитический, табличный, графический.
1). Аналитический способ: функция задается в виде одной или нескольких формул или уравнений. Например, 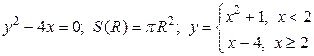 .
.
Если область определения функции  не указана, то предполагается, что она совпадает с множеством всех значений аргумента, при которых соответствующая формула имеет смысл. Так, область определения функции
не указана, то предполагается, что она совпадает с множеством всех значений аргумента, при которых соответствующая формула имеет смысл. Так, область определения функции 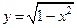 является отрезок
является отрезок 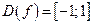 . Аналитический способ задания функции является наиболее совершенным, так как к нему приложены методы математического анализа, позволяющие полностью исследовать функцию
. Аналитический способ задания функции является наиболее совершенным, так как к нему приложены методы математического анализа, позволяющие полностью исследовать функцию  .
.
2). Графический способ: задается график функции.
Значения функции y, соответствующие тем или иным значениям аргумента x, непосредственно находятся из этого графика. Преимуществом графического задания является наглядность, недостатком – его неточность.
3). Табличный способ: функция задается таблицей ряда значений аргумента и соответствующих значений функции. Например, известные таблицы значений тригонометрических функций. На практике часто приходится пользоваться таблицами значений функций, полученных опытным путем или в результате наблюдений. По экспериментальным данным можно составить функцию, записанную аналитически. Для составления функции используется метод наименьших квадратов, с которым познакомимся в разделе «Математическая статистика».
Производной функции
Понятие производной является одним из основных понятий дифференциального исчисления. Впервые это понятие появилось в работах Лейбница, Ньютона, Лагранжа. Производная широко применяется при решении целого ряда задач математики, физики, экономики и других наук, в особенности при изучении скорости разных процессов.
Рассмотрим некоторые задачи, приводящие к понятию производной.
Касательная к кривой
Пусть дана некоторая плоская кривая L. Возьмем на ней некоторую фиксированную точку  . Если точка
. Если точка 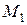 , отличная от
, отличная от 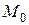 , тоже принадлежит кривой L, то прямая
, тоже принадлежит кривой L, то прямая 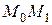 называется секущей. Будем перемещать
называется секущей. Будем перемещать 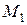 вдоль L так, чтобы
вдоль L так, чтобы 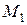 стремилась к совпадению с
стремилась к совпадению с 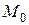 . Секущая будет менять свое положение в зависимости от положения
. Секущая будет менять свое положение в зависимости от положения 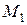 . Предельное положение секущей
. Предельное положение секущей 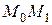 (если оно существует) при
(если оно существует) при 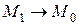 называется касательной к кривой L в точке
называется касательной к кривой L в точке 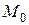 .
.
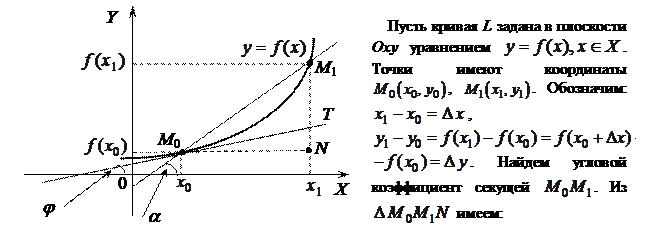
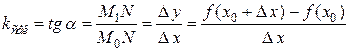 .
.
При 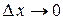 в силу непрерывности функции приращение
в силу непрерывности функции приращение 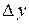 тоже стремится по кривой к нулю; поэтому точка
тоже стремится по кривой к нулю; поэтому точка 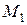 неограниченно приближается по кривой к точке
неограниченно приближается по кривой к точке 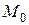 , а секущая
, а секущая 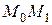 , поворачиваясь около точки
, поворачиваясь около точки 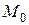 , переходит в касательную
, переходит в касательную 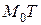 .
.
Угол 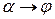 , т.е.
, т.е. 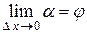 . Следовательно,
. Следовательно, 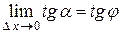 . Поэтому угловой коэффициент касательной равен:
. Поэтому угловой коэффициент касательной равен:
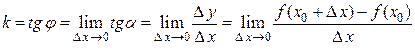 ,
,
если этот предел существует и конечен.
Производная функции в точке
Пусть функция  определена в некоторой окрестности точки
определена в некоторой окрестности точки  , где
, где 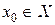 .
.
Чтобы найти производную функции в точке  , необходимо проделать следующие операции:
, необходимо проделать следующие операции:
- аргументу
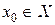 дадим приращение
дадим приращение 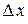 , т.е.
, т.е. 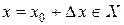 ;
; - найдем соответствующее приращение функции
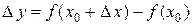 ;
; - составим отношение приращения функции к приращению аргумента
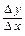 ;
; - найдем предел этого отношения при
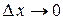 , т.е.
, т.е. 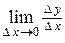
Если этот предел существует, то его называют производной функции  и обозначают:
и обозначают: 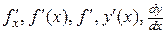 .
.
Определение 3.1. Производной функции  в точке
в точке  называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю, т.е.
называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю, т.е.
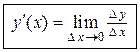 (3.1)
(3.1)
или
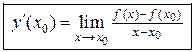 . (3.2)
. (3.2)
Нахождение производной функции  называется дифференцированием этой функции. Функция, имеющая производную в точке
называется дифференцированием этой функции. Функция, имеющая производную в точке  , называется дифференцируемой в этой точке. Функция, дифференцируемая во всех точках множества X, называется дифференцируемой на этом множестве.
, называется дифференцируемой в этой точке. Функция, дифференцируемая во всех точках множества X, называется дифференцируемой на этом множестве.
Значение производной функции  в точке
в точке  обозначается одним из символов:
обозначается одним из символов: 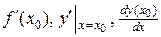 .
.
Пример 3.1. Найти значение производной функции  в точке
в точке  , используя определение производной функции:
, используя определение производной функции:
1) 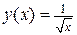 ,
, 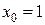 ; 3)
; 3) 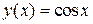 ,
, 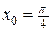 ;
;
2) 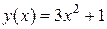 ,
, 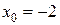 ; 4)
; 4) 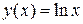 ,
, 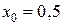 .
.
Решение. 1) I способ: используем формулу 1.2:
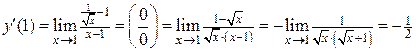 .
.
II способ: используем формулу 1.1:
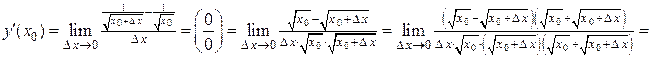
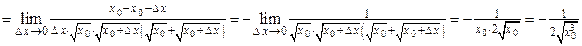 .
.
Таким образом,
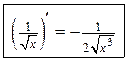 .
.
Находим значение производной функции в точке 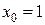 :
:
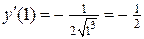 .
.
2) Воспользуемся формулой 3.1:
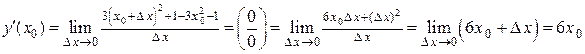 .
.
Таким образом,
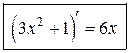 .
.
Находим значение производной функции в точке 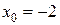 :
:
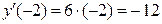 .
.
3) Воспользуемся формулой 3.1:
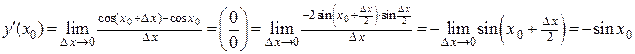
Таким образом,
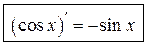 .
.
Находим значение производной функции в точке 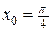 :
: 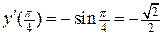 .
.
4) Воспользуемся формулой 3.1:
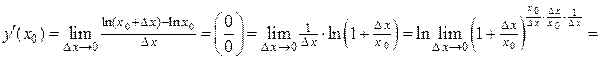
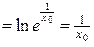 .
.
Таким образом,
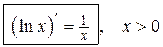 .
.
Находим значение производной функции в точке 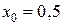 :
: 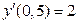 .
.
,
Выше была рассмотрена задача про касательную к кривой, в которой был найден угловой коэффициент касательной:
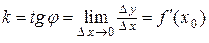 .
.
Это дает возможность сформулировать геометрический смысл производной функции в точке: производная 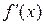 в точке
в точке  равна угловому коэффициенту касательной к графику функции
равна угловому коэффициенту касательной к графику функции  в точке, абсцисса которой равна
в точке, абсцисса которой равна  :
:
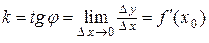 .
.
Механический смысл: скорость прямолинейного движения материальной точки в момент время 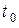 есть производная от пути
есть производная от пути 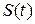 по времени
по времени 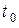 :
:
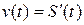 .
.
Физический смысл: если функция  описывает какой-либо процесс, то производная
описывает какой-либо процесс, то производная 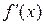 есть скорость протекания этого процесса.
есть скорость протекания этого процесса.
3.3.Связь между непрерывностью и
Дифференцируемостью функции
Определяя понятие производной функции в точке  , мы предполагали лишь существование функции в точке
, мы предполагали лишь существование функции в точке  и в некоторой достаточно малой ее окрестности, и существование предела
и в некоторой достаточно малой ее окрестности, и существование предела 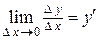 . Теперь свяжем дифференцируемость функции в точке с непрерывностью этой функции.
. Теперь свяжем дифференцируемость функции в точке с непрерывностью этой функции.
Теорема 3.1. Если функция  определена на X и в точке
определена на X и в точке 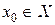 имеет конечную производную
имеет конечную производную 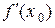 , то
, то 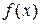 непрерывна в точке
непрерывна в точке  .
.
Из теоремы 3.1. следует, что в точках разрыва функции  производная не существует.
производная не существует.
Неверно утверждение, обратное к теореме 3.1.: из непрерывности функции в точке не следует существование производной в этой точке.
Например, функция 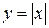 в точке
в точке 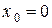 непрерывна, но производная не существует, т.к.
непрерывна, но производная не существует, т.к.
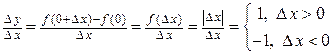 .
.
Это значит, график функции не имеет касательной в точке  .
.
Хотя  для функции
для функции 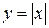 не существует, но существуют односторонние пределы:
не существует, но существуют односторонние пределы: 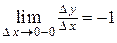 и
и 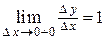 . В этом случае говорят, что функция имеет односторонние производные.
. В этом случае говорят, что функция имеет односторонние производные.
Односторонними производными (производными слева и справа) называют 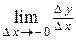 и
и 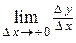 , если они существуют. Обозначаются соответственно:
, если они существуют. Обозначаются соответственно: 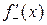 и
и 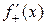 .
.
Если 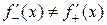 , то производная в точке не существует.
, то производная в точке не существует.
Надо заметить, что производная 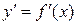 непрерывной функции
непрерывной функции  сама не обязательно является непрерывной.
сама не обязательно является непрерывной.
Например, функция 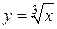 определена для
определена для 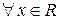 , т.е.
, т.е. 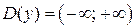 . По определению 3.1.
. По определению 3.1. 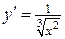 . В точке
. В точке 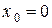 производная функции равна
производная функции равна 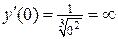 , хотя сама функция в точке
, хотя сама функция в точке 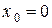 непрерывна.
непрерывна.
Если 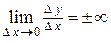 , то производная называется бесконечной.
, то производная называется бесконечной.
Если функция  имеет непрерывную производную
имеет непрерывную производную 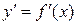 в некотором интервале
в некотором интервале 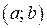 , то функция называется гладкой.
, то функция называется гладкой.
3.4.Основные правила дифференцирования.
Дифференцирование функций,
Заданных параметрически
Кроме того, что функция может быть задана в явном или неявном виде, есть функции, которые можно задать параметрически.
Если зависимость между аргументом x и функцией y задана в виде уравнений
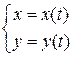 ,
,
где t – вспомогательная переменная, называемая параметром, то говорят, что «функция задана параметрически».
Например, 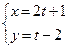 задает линейную функцию
задает линейную функцию 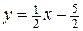 , которую можно получить, если из первого уравнения выразить t и подставить во второе.
, которую можно получить, если из первого уравнения выразить t и подставить во второе.
Теорема 3.5. Пусть функция задана параметрически
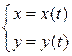 ,
,
и функции 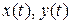 дифференцируемы в области определения переменной t, тогда
дифференцируемы в области определения переменной t, тогда
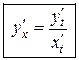 . (3.3)
. (3.3)
Пример 3.7. Пусть 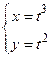 . Найти
. Найти 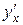 .
.
Решение. Имеем 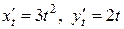 .
.
Следовательно, 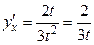 .
.
,
В этом можно убедиться, если найти непосредственно зависимость y от x. Действительно, 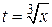 . Тогда
. Тогда 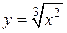 . Отсюда
. Отсюда 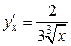 , т.е.
, т.е. 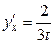 .
.
Пример 3.8. Пусть 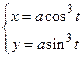 . Найти
. Найти 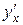 в точке
в точке 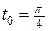 .
.
Решение. Используя формулу (3.3), находим
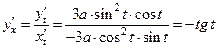 .
.
Далее получаем
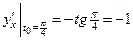 .
.
,
3.8. Производные высших порядков
Производная 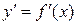 функции
функции  есть также функция от x и называется производной первого порядка.
есть также функция от x и называется производной первого порядка.
Если функция 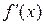 дифференцируема, то ее производная называется производной второго порядкаи обозначается:
дифференцируема, то ее производная называется производной второго порядкаи обозначается: 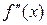 или
или 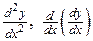 . Итак,
. Итак,
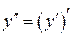 .
.
Производная от производной второго порядка, если она существует, называется производной третьего порядка и обозначается: 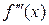 или
или 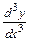 . Итак,
. Итак,
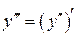 .
.
Производная n-го порядка (или n-й производной) называется производная от производной 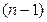 порядка:
порядка:
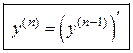 . (3.4)
. (3.4)
Производная порядка выше первого называются производными высших порядков. Начиная с производной четвертого порядка, производные обозначаются римскими цифрами или числами в скобках, например, 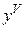 или
или 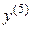 – производная пятого порядка.
– производная пятого порядка.
Пример 3.9. Найти значение производной 4-го порядка для функции
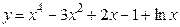 при
при 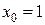 .
.
Решение. Находим последовательно
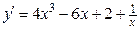 ;
;
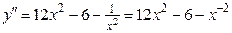 ;
;
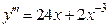 ;
;
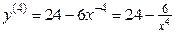 .
.
Следовательно, 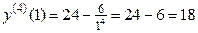 .
.
,
Пример 3.10. Найти производную n-го порядка для функции 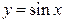 .
.
Решение. Находим последовательно
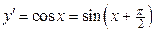 ;
;
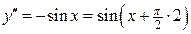 ;
;
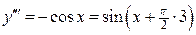 ;
;
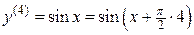 ;
;
…………………….
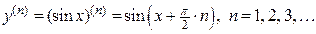 . ,
. ,
Отметим, что в формуле (3.4) принято 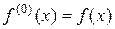 , т.е. производная нулевого порядка есть сама функция.
, т.е. производная нулевого порядка есть сама функция.
Пусть материальная точка движется прямолинейно по закону 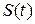 . Как известно, производная первого порядка
. Как известно, производная первого порядка 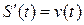 .
.
Механический смысл производной второго порядка: вторая производная от пути по времени есть величина ускорения прямолинейного движения материальной точки, т.е. 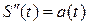 .
.
Пусть функция  задана неявно в виде уравнения
задана неявно в виде уравнения 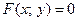 .
.
Продифференцировав это уравнение по x, и разрешив полученное уравнение относительно 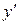 , найдем производную первого порядка. Продифференцировав по x первую производную, получим вторую производную от неявной функции. В нее войдут x, y и
, найдем производную первого порядка. Продифференцировав по x первую производную, получим вторую производную от неявной функции. В нее войдут x, y и 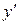 . Подставляя уже найденное значение
. Подставляя уже найденное значение 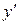 в выражение второй производной, выразим
в выражение второй производной, выразим 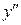 через x и y.
через x и y.
Аналогично поступаем для нахождения производной третьего (и выше) порядка.
Его геометрический смысл
Пусть дана функция  , определенная на множестве X, и в точке
, определенная на множестве X, и в точке 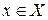 имеет отличную от нуля производную, т.е.
имеет отличную от нуля производную, т.е. 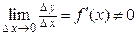 . Тогда по теореме о связи функции, ее предела и б.м.ф., можно записать
. Тогда по теореме о связи функции, ее предела и б.м.ф., можно записать 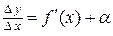 , где
, где 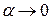 при
при 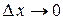 , или
, или 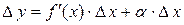 .
.
Таким образом, приращение функции 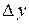 представляет собой сумму двух слагаемых
представляет собой сумму двух слагаемых 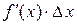 и
и 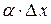 , являющиеся бесконечно малыми при
, являющиеся бесконечно малыми при 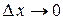 . При этом первое слагаемое есть бесконечно малая функция одного порядка с
. При этом первое слагаемое есть бесконечно малая функция одного порядка с 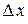 , так как
, так как 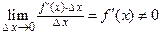 , а второе слагаемое есть бесконечно малая функция более высокого порядка, чем
, а второе слагаемое есть бесконечно малая функция более высокого порядка, чем 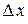 , так как
, так как 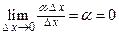 .
.
Слагаемое 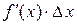 называют главной частью приращения функции
называют главной частью приращения функции 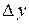 .
.
Определение 4.1. Дифференциалом функции  в точке x называется главная часть ее приращения, равная произведению производной функции на приращение аргумента, и обозначается
в точке x называется главная часть ее приращения, равная произведению производной функции на приращение аргумента, и обозначается 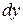 (или
(или 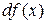 ):
):
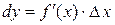 . (4.1)
. (4.1)
Дифференциал 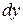 называют также дифференциалом первого порядка. Найдем дифференциал независимой переменной x, т.е. дифференциал функции
называют также дифференциалом первого порядка. Найдем дифференциал независимой переменной x, т.е. дифференциал функции 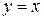 . Так как
. Так как 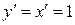 , то согласно формуле (2.1), имеем
, то согласно формуле (2.1), имеем 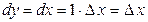 , т.е. дифференциал независимой переменной равен приращению этой переменной:
, т.е. дифференциал независимой переменной равен приращению этой переменной: 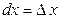 . Поэтому формулу (2.1) можно записать так:
. Поэтому формулу (2.1) можно записать так:
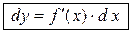 , (4.2)
, (4.2)
иными словами, дифференциал функции равен произведению производной этой функции на дифференциал независимой переменной.
Из формулы (4.2) следует равенство 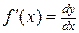 . Теперь обозначение производной можно рассматривать как отношение дифференциалов
. Теперь обозначение производной можно рассматривать как отношение дифференциалов 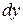 и
и 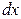 .
.
Пример 4.1. Найти дифференциал функции
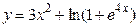
а) в общем виде;
б) в точке 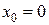 ;
;
в) при 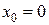 и
и 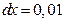 .
.
Решение. Находим производную первого порядка:
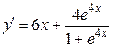 .
.
а) Используя формулу (4.2), получаем
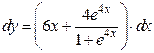 .
.
б) Дифференциал функции в точке равен
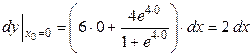 .
.
в) При 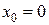 и
и 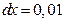 получаем:
получаем:
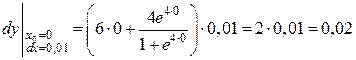 .
.
,
Выясним геометрический смысл дифференциала функции.
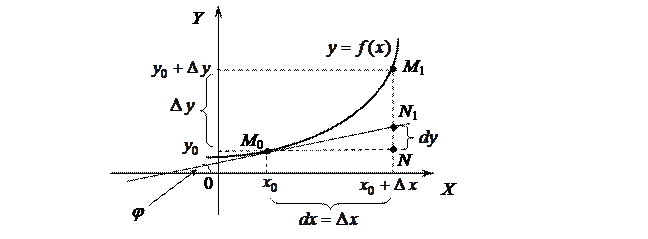
Проведем к графику функции  в точке
в точке  касательную
касательную  и рассмотрим ординату этой касательной для точки
и рассмотрим ординату этой касательной для точки 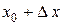 . На рисунке
. На рисунке 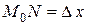 ,
, 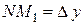 . Из прямоугольного треугольника
. Из прямоугольного треугольника 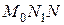 имеем:
имеем:
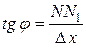 , т.е.
, т.е. 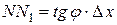 .
.
Но, согласно геометрическому смыслу производной, 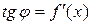 . Поэтому
. Поэтому 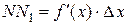 .
.
Сравнивая полученный результат с формулой (2.1.), получаем 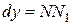 .
.
Геометрический смысл: дифференциал функции  в точке x равен приращению ординаты касательной к графику функции в этой точке, когда x получит приращение
в точке x равен приращению ординаты касательной к графику функции в этой точке, когда x получит приращение 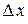 .
.
Правила вычисления дифференциала аналогичны соответствующим правилам нахождения производной.
Инвариантность формы записи дифференциала
Пусть  для
для 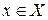 , тогда
, тогда
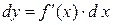 .
.
Рассмотрим сложную функцию 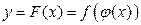 , где
, где 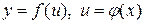
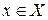 , причем
, причем 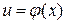 и
и 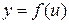 дифференцируемы соответственно в точках x и
дифференцируемы соответственно в точках x и 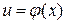 . Тогда
. Тогда 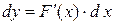 , но
, но 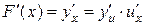 следовательно,
следовательно, 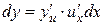 . А так как
. А так как 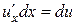 , то
, то
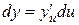 .
.
Таким образом, форма записи дифференциала сохраняется, если независимую переменную заменить некоторой функцией. Это свойство называется инвариантностью (неизменностью) формы записи дифференциала.
Заметим, что из инвариантности следует, что, хотя 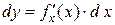 (x – независимая переменная), а
(x – независимая переменная), а 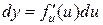 (
( 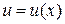 – функция), запись их одинакова. Однако сущность этих формул различна:
– функция), запись их одинакова. Однако сущность этих формул различна: 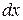 задается произвольно,
задается произвольно, 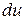 же задавать произвольно, вообще говоря, нельзя;
же задавать произвольно, вообще говоря, нельзя; 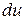 нужно вычислить по формуле дифференциала
нужно вычислить по формуле дифференциала 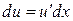 . Это относится и к случаю с несколькими промежуточными функциями.
. Это относится и к случаю с несколькими промежуточными функциями.
Точки экстремума
| В мире не происходит ничего, в чем бы не был виден смысл какого-нибудь максимума или минимума. Л. Эйлер |
Процессы, происходящие в механике, физике, химии, термодинамике, экономике, очень часто описываются функциями, заданными формулами. Чтобы знать характеристики рассматриваемого процесса, следует изучить характеристики функций, описывающих процесс, а для наглядности рассмотреть функции в их графическом задании. Но чаще интерес представляет не графическое задание функции, а качественное поведение графика функции без соблюдения масштабных размеров для достаточно точного (приближенного с заданной точностью) определения значений функции. Эти качественные свойства функций можно описать, используя методы дифференциального исчисления.
Теорема 5.1 (условие монотонности функции). Пусть функция 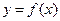 определена на X и внутри имеет конечную производную
определена на X и внутри имеет конечную производную 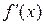 . Для того чтобы
. Для того чтобы 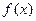 была монотонно возрастающей (убывающей), достаточно, чтобы
была монотонно возрастающей (убывающей), достаточно, чтобы 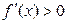 (
( 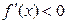 ) для всех x внутри X.
) для всех x внутри X.
Теорему примем без доказательства.
Если функция 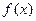 , определенная и непрерывная на множестве X, не является монотонной, то найдутся такие части промежутка X, что наибольшее или наименьшее значение достигается функцией во внутренней точке.
, определенная и непрерывная на множестве X, не является монотонной, то найдутся такие части промежутка X, что наибольшее или наименьшее значение достигается функцией во внутренней точке.
Определение 5.1. Функция 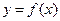 имеет в точке
имеет в точке  максимум (минимум), если существует такая окрестность точки
максимум (минимум), если существует такая окрестность точки 
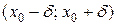 , не выходящая из области определения функции, что для всех
, не выходящая из области определения функции, что для всех 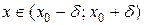
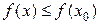
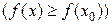 .
.
Максимум и минимум называют общим термином «экстремум».
Из определения экстремума следует, что вне окрестности точки максимума  значения функции могут быть больше этого максимума. Поэтому такой максимум называется локальным (местным). Аналогично определяется локальный минимум. Точки локального максимума и минимума называются точками локального экстремума, а значения функции в них – локальными экстремумами функции.
значения функции могут быть больше этого максимума. Поэтому такой максимум называется локальным (местным). Аналогично определяется локальный минимум. Точки локального максимума и минимума называются точками локального экстремума, а значения функции в них – локальными экстремумами функции.
Если функция 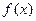 определена на отрезке
определена на отрезке 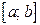 и имеет локальный экстремум на каком-то из концов этого отрезка, то такой экстремум будем называть локальным односторонним или краевым экстремумом. В этом случае соответствующая окрестность является правой для a и левой для b полуокрестностью.
и имеет локальный экстремум на каком-то из концов этого отрезка, то такой экстремум будем называть локальным односторонним или краевым экстремумом. В этом случае соответствующая окрестность является правой для a и левой для b полуокрестностью.

Рассмотрим условия существования экстремума функции. Необходимое условие экстремума примем без доказательства.
Теорема 5.2 (необходимое условие экстремума). Если дифференцируемая функция 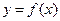 имеет экстремум в точке
имеет экстремум в точке  , то ее производная в этой точке равна нулю:
, то ее производная в этой точке равна нулю: 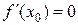 .
.
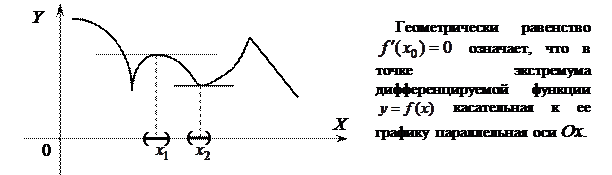
Отметим, что обратная теорема неверна, т.е. если 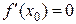 , то это не значит, что
, то это не значит, что  – точка экстремума.
– точка экстремума.
Точки, в которых производная равна нулю, называются стационарными (критическими или «подозрительными» на экстремум). Точки, в которых функция непрерывна, но производная не существует или бесконечна, также являются критическими, так как это тоже точки, где может быть экстремум.
Например, для функции 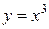 ее производная
ее производная 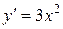 рав
рав
