Статистическая проверка непараметрических гипотез

Для того чтобы выяснить, подчиняются ли экспериментальные данные какому-либо закону распределения, надо сформулировать статистическую гипотезу в отношении распределения анализируемой случайной величины и затем проверить ее. Для проверки гипотез, выдвигаемых в отношении вида распределения, используются специ­альные статистики, называемые непараметрическими критериями или критериями согласия. Рассмотрим процесс проверки непараметриче­ской гипотезы с помощью одного из критериев согласия - критерия Пирсона. На первом этапе следует выдвинуть нулевую гипотезу, со­стоящую в том, что анализируемый признак подчиняется какому-либо закону распределения. Далее, исходя из предположения о том, что нулевая гипотеза справедлива, следует вычислить статистику :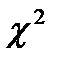

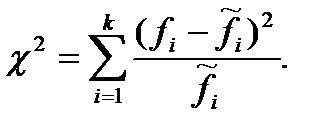(6)

Таблица 11 ─ Вычисление теоретических частот для функции нормального распределения (высоты)

xi		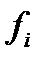tiн	tiв	Ф(tiн)	Ф(tiв)	Рi		∆ -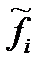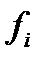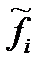
16,8		-3,51	-3,12		0,001	0,001	0,2	-0,2
17,7		-3,12	-2,73	0,001	0,003	0,002	0,4	3,6
18,6		-2,73	-2,34	0,003	0,01	0,007	1,4	1,6
19,5		-2,34	-1,95	0,01	0,026	0,016	3,2	0,8
20,4		-1,95	-1,56	0,026	0,059	0,033	6,6	-1,6
21,3		-1,56	-1,17	0,059	0,121	0,062	12,4	-5,4
22,2		-1,17	-0,78	0,121	0,218	0,097	19,4	-3,4
23,1		-0,78	-0,39	0,218	0,348	0,13		-7
		-0,39	0,00	0,348	0,5	0,152	30,4	-0,4
24,9		0,00	0,39	0,5	0,652	0,152	30,4	-4,4
25,8		0,39	0,77	0,652	0,779	0,127	25,4	19,6
26,7		0,77	1,16	0,779	0,877	0,098	19,6	5,4
27,6		1,16	1,55	0,877	0,939	0,062	12,4	-0,4
28,5		1,55	1,94	0,939	0,974	0,035		-5
29,4		1,94	2,33	0,974	0,99	0,016	3,2	-1,2
30,3		2,33	2,72	0,99		0,01		-2
Сумма

Полученное значение сравнивается с квантилем распределения Пирсона χ², приведенного в табл. 5 приложения. В качестве парамет­ров распределения используется уровень значимости (обычно исполь­зуется α= 0,05) и число степеней свободы:

γ=k-ρ-1, (7)

где k - общее число степеней свободы, равное числу слагаемых в сумме из формулы (7); ρ - число параметров теоретической функции распределения, которые оценивались по анализируемым данным.

При вычислении критерия Пирсона следует иметь в виду, что теоретические частоты не должны быть меньше пяти. В том случае, если теоретические частоты оказываются недостаточно большими, следует объединять маленькие классы в большие.

Рассмотрим процесс проверки непараметрической гипотезы cпомощью критерия Пирсона на примере распределений диаметров, и высот деревьев в сосновом древостое. Нулевая гипотеза будет заключаться в предположении, что анализируемые случайные величины подчиняются закону нормального распределения. Исходя из такого предположения, вычислим статистику χ²для вариационного ряда по диаметрам.

Таблица 12 ─ Вычисления критерия согласия Пирсона χ² (диаметры)

xi		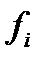	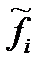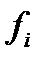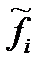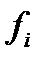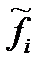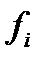-	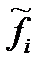( - )2	( - )2/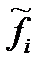
До укрупнения	После укрупнения	До укрупнения	После укрупнения
12,7			3,
15,6			4,4	7,4	-7,4	54,76	7,4
18,5			8,2	8,2	1,8	3,24	0,4
21,4			14,2	14,2	3,8	14,44	1,02
24,3			21,2	21,2	5,8	33,64	1,59
27,2			26,2	26,2	5,8	33,64	1,28
30,1			30,0	30,0	1,0	2,0	0,03
33,0			29,0	29,0	-10,0	100,0	3,45
35,9			23,8	23,8	0,2	0,04	0,02
38,8			17,8	17,8	0,2	0,04	0,01
41,7			11,2	11,2	-5,2	27,04	2,41
44,6			6,2	11,0	4,0	16,0	1,5
47,5			3,0
50,4			1,2
53,3			0,6
Сумма			200,0	200,0			19,05

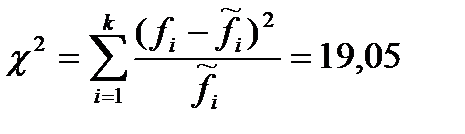
Далее следует объединить интервалы таким образом, чтобы теоретические частоты в укрупненных классах были не меньше пяти. Дальнейшие расчеты (три последние колонки табл. 14) выполняем, используя эм­пирические и теоретические частоты, полученные после укрупнения классов. Сумма, полученная в последней колонке таблицы, и будет статистикой Пирсона χ². Теперь, пользуясь табл. 5 приложения, най­дем соответствующий квантиль распределения Пирсона χ², чтобы, сравнивая его с вычисленной статистикой χ², проверить нулевую ги­потезу. Уровень значимости (вероятность отклонения правильной нулевой гипотезы) возьмем α = 0,05. С учетом объединения интерва­лов и того, что мы оценили два параметра нормального распределения (σ и m)по материалам наших экспериментальных данных, вычислим число степеней свободы, пользуясь формулой (7):

γ=k-ρ-1=11-2-1=8

Определив необходимые параметры, найдем квантиль распределения Пирсона χ²_0.05;8=15,507 по табл. 5 прил. Так как вычисленная статистика Пирсона χ²= 19,05 превышает табличное значение, то мы отклоняем нулевую гипотезу, т. е. распределение диаметров деревьев в древостое не подчиняется закону нормального распределения.

Таблица 13 ─ Вычисления критерия согласия Пирсона χ² (высоты)

xi		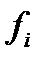	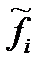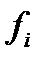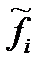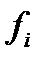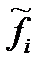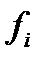-	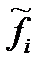( - )2	( - )2/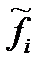
До укрупнения	После укрупнения	До укрупнения	После укрупнения
16,8			0,2
17,7			0,4
18,6			1,4
19,5			3,2	5,2	5,8	33,64	6,469230769
20,4			6,6	6,6	-1,6	2,56	0,387878788
21,3			12,4	12,4	-5,4	29,16	2,351612903
22,2			19,4	19,4	-3,4	11,56	0,595876289
23,1					-7		1,884615385
			30,4	30,4	-0,4	0,16	0,005263158
24,9			30,4	30,4	-4,4	19,36	0,636842105
25,8			25,4	25,4	19,6	384,16	15,12440945
26,7			19,6	19,6	5,4	29,16	1,487755102
27,6			12,4	12,4	3,6	12,96	1,04516129
28,5
29,4			3,2	5,2
30,3
Сумма			200,0	200,0			29,989

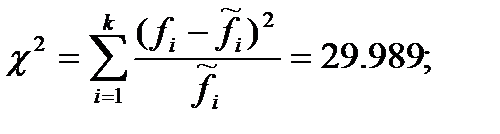γ=k-ρ-1=12-2-1=9

Сравнивая полученную статистику Пирсона χ²= 29,989 с кванти­лем распределения Пирсона χ²_0.05;9=16,919, приходим к выводу, что и в данном случае не следует принимать нулевую гипотезу, так как вычис­ленное значение превышает табличное. Таким образом, и распределе­ние высот деревьев в сосновом древостое не подчиняется закону нор­мального распределения.