Статистические ряды и их графическое изображение

Введение

Лесная биометрия решает задачи обработки массовых (статистических) данных. Экспериментальные материалы, собранные в лесу, как раз и являются таковыми. Как правило, они представлены в виде числовых значений, характеризующих различные лесные объекты (высота, диаметр или объем дерева; число шишек на дереве; количество семян в шишке и т. д.). В связи с этим предметом лесной биометрии являются различные случайные величины, характеризующие сообщества.

Основная задача лесной биометрии – количественный и качественный анализ массовых случайных явлений, имеющих место в лесных биогеоценозах. Такая процедура подразумевает ряд этапов: организация и планирование наблюдений; сбор экспериментальных данных; свертка информации, т. е. сведения большого количества исходных данных к небольшому числу параметров, которые в сжатом виде характеризуют всю исследуемую совокупность; анализ экспериментальных данных; принятие решений на основе результатов такого анализа; прогнозирование случайных явлений.

Статистические ряды и их графическое изображение

Составление таблицы распределения

Наряду с простой группировкой данных в интервале вариационные ряды в некоторых случаях целесообразно сгруппировать данные сразу по двум параметрам. Эта потребность, как правило, возникает в том случае, если необходимо проанализировать связь между двумя случайными величинами. В таких случаях составляют так называемые таблицы распределения (корреляционные таблицы, корреляционные решетки). Таблица 4.

Для примера составим таблицу распределения 200 деревьев по интервалам диаметра и высоты в чистом сосновом древостое. Для этого воспользуемся интервалами рядов распределения деревьев по диаметрам и высотам. Впишем границы интервалов вариационного ряда по диаметрам в первую строку таблицы, а границы вариационного ряда по высотам – в первую колонку. Затем, распределяя наблюдения одновременно по интервалам диаметров и высот и регистрируя их методом конвертов, определим частоты каждой клетки корреляционной решетки.

Показатели вариации

Средние величины указывают на то значение признака, вокруг которого группируются анализируемые наблюдения. Однако вокруг одного и того же значения признака наблюдения могут располагаться совершенно по-разному. Для того чтобы отразить характер располо­жения наблюдений вокруг среднего, и служат показатели вариации. Рассмотрим некоторые из них.

Размах вариации.Это наиболее простой показатель, характери­зующий распределение вариант вокруг среднего. Он вычисляется как разность между максимальным и минимальным значениями признака, которые в биометрии называют также лимитами(от латинского слова limes - предел) и обозначают символом lim:

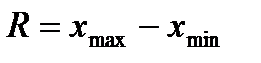
Если наблюдения плотно группируются вокруг среднего, то ли­миты располагаются близко друг к другу и размах вариации оказыва­ется небольшим. Если же разброс данных велик, то, как правило, минимальная и максимальная варианты располагаются далеко друг от друга и размах вариации получается большим.

Однако размах вариации является ненадежным показателем, так как он вычисляется на основании значений лимитов, а последние, в свою очередь, являются очень неустойчивыми статистиками и могут значительно варьировать от выборки к выборке. Кроме того, так как при вычислении размаха вариации используются только две крайние варианты, то он не дает нам никакой информации о характере распре­деления всех остальных вариант, располагающихся ближе к среднему.

Эмпирическая дисперсия.Этот показатель получил свое назва­ние от латинского слова dispersio - рассеяние. Это не что иное, как средний квадрат отклонений вариант от среднего арифметического. Вычисляется дисперсия так:

,

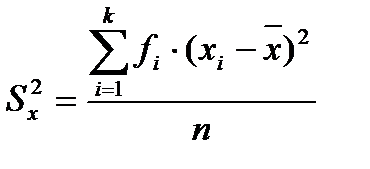Выборочная дисперсия, рассчитанная по формуле, дает сме­щенную оценку генеральной дисперсии. Для того чтобы получить несмещенную оценку, в формулу необходимо добавить сомножитель 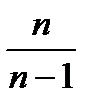, называемый поправкой Бесселя:

,

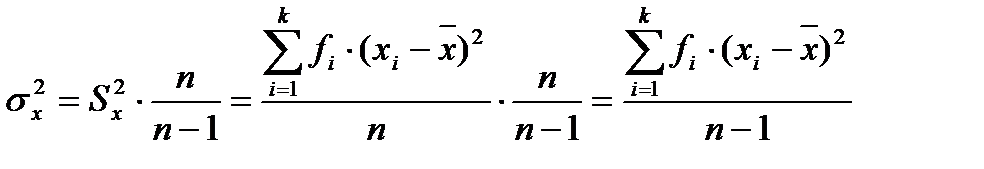Величина n—1 из формулы называется числом степеней свободы. Она показывает, сколько в данном случае имеется независи­мых наблюдений.

Среднеквадратическое отклонение.Дисперсия часто применя­ется для оценки вариации данных, однако иногда для характеристики изменчивости признака удобнее использовать среднеквадратическое отклонение, которое

является квадратным корнем из дисперсии:

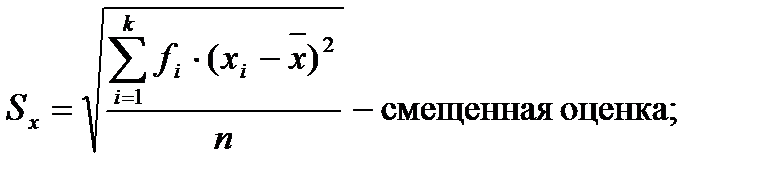
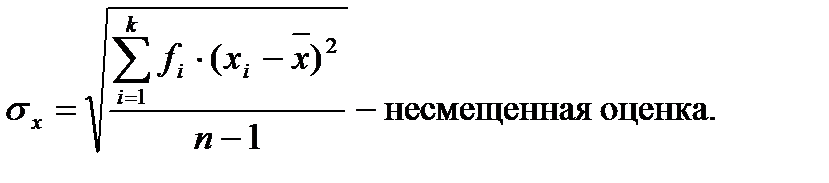
В отличие от дисперсии, среднеквадратическое отклонение вы­ражается в тех же единицах измерения, что и анализируемый признак. В связи с этим данный показатель является более естественным и легче поддается анализу.

Коэффициент вариации.Дисперсия и среднеквадратическое от­клонение довольно полно характеризуют вариацию, однако часто удобнее иметь показатель, оценивающий разброс данных не в абсо­лютных величинах, а в относительных. Таким показателем является коэффициент вариации. Он показывает, сколько процентов составляет среднеквадратическое отклонение от среднего арифметического:

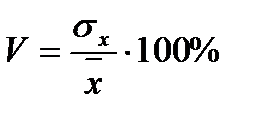
В биометрии этот показатель часто оказывается весьма полез­ным. Дело в том, что анализу подвергаются, как правило, объекты живой природы, а они с течением времени изменяют свои размеры, растут. В связи с этим часто необходимо анализировать выборки, сделанные для объектов с разным средним возрастом, а следователь­но, и с разными средними размерами. Если в таких случаях необхо­димо сравнить степень изменчивости признака в разных выборках, то удобнее оперировать коэффициентом вариации, так как он даст нам величину вариации по отношению к среднему значению.

Коэффициент асимметрии.Рассмотренные выше показатели довольно полно характеризуют анализируемые признаки, однако ни один из них не отражает степень симметричности распределения наблюдений относительно среднего значения.

Для того чтобы оценить степень такой неравномерности рас­пределения наблюдений относительно среднего арифметического, используют коэффициент асимметрии, который можно вычислить по формуле:

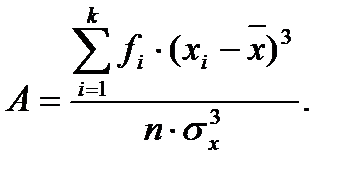
Коэффициент асимметрии может принимать как положитель­ные, так и отрицательные значения. В том случае, если левая ветвь распределения более пологая и длинная, а вершина кривой смещена вправо относительно среднего арифметического, то коэффициент асимметрии для такого распределения имеет отрицательное значение. Такая асимметрия называется левосторонней или отрицательной.

Если распределение имеет более длинную и пологую правую ветвь, а его вершина смещена влево относительно среднего арифме­тического, то в таком случае имеет место правосторонняя, или поло­жительная, асимметрия. Коэффициент асимметрии в таком случае будет положительным.

Эмпирический коэффициент эксцесса. Кроме того, что распре­деления наблюдений могут отличаться друг от друга по степени асимметричности, они могут иметь разную крутизну. Распределения могут быть островершинными и плосковершинными. В случае остро­вершинной кривой, когда большое число наблюдений группируется в непосредственной близости от центра распределения, говорят о нали­чии положительного эксцесса. Кривая распределения имеет отрица­тельный эксцесс, если она является плосковершинной. Для оценки степени крутизны кривой распределения используется коэффициент эксцесса, который вычисляется по формуле:

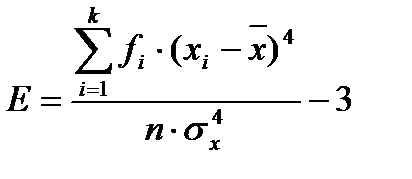
Этот коэффициент построен таким образом, что его значение для нормального распределения, как для наиболее изученного и часто используемого, равен нулю. В том случае, если коэффициент эксцесса принимает положительное значение (положительный эксцесс), рас­пределение вариант будет более крутым, чем нормальное распределе­ние. Когда этот показатель меньше нуля (отрицательный эксцесс), наблюдения будут образовывать более плосковершинную кривую, чем нормальное распределение.

Эмпирические моменты.Кроме рассмотренных выше показате­лей, для характеристики массовых данных используется система ста­тистик, называемых моментами. Если с - константа, то выражением:

,

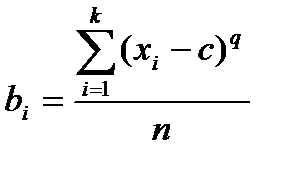задается момент относительно точки с порядка q.

Моменты, вычисленные относительно средней арифметической 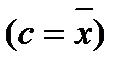, называются центральными:

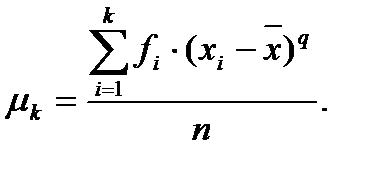
Для того чтобы определить остальные показатели вариации, со­ставим по данным вариационных рядов диаметров и высот вспомога­тельные таблицы.

Таблица 7 ─ Вычисление показателей вариации (диаметры)

Xi	fi	xi − x.	(xi − x)2	(xi − x)3 ⋅fi	(xi − x)4 ⋅ fi
15,6		-15,524	722,98	-11223,54	174234,24
18,5		-12,354	1068,34	-13198,27	163051,43
21,4		-9,454	1608,80	-15209,59	143791,46
24,3		-6,55	1158,37	-7587,32	49696,95
27,2		-3,65	426,32	-1556,07	5679,66
30,1		-0,75	17,44	-13,08	9,81
		2,15	87,83	188,83	405,98
35,9		5,05	612,06	3090,90	15609.05
38,8		7,95	1137,64	9044,23	71901,63
41,7		10,85	706,335	7663,73	83151,47
44,6		13,75	756,25	10398,44	142978,55
47,5		16,65	1940,55	32310,16	537964,164
50,4		19,55	1528,81	29888,24	584315,09
Сумма		27,938	11771,73	43796,66	1972789,48

Таблица 8 ─ Вычисление показателей вариации (высоты)

Xi	fi	xi − x.	(xi − x)2	(xi − x)3 ⋅fi	(xi − x)4 ⋅ fi
17,7		-6,76	182,79	-1235,66	8353,06
18,6		-5,86	103,01	-603,69	3537,62
19,5		-4,96	98,41	-488,09	2420,95
20,4		-4,06	82,42	-334,61	1358,64
21,3		-3,16	69,90	-220,88	697,98
22,2		-2,26	81,72	-184,69	417,40
23,1		-1,36	35,14	-47,79	64,99
		-0,46	6,35	-2,92	1,34
24,9		0,43	4,81	2,06	0,88
25,8		1,33	79,60	105,86	140,81
26,7		2,23	124,32	277,24	618,24
27,6		3,13	117,56	367,97	1151,75
28,5		4,03	32,48	130,90	527,52
29,4		4,93	49,20	242,57	1195,87
Сумма		-9,16	1067,71	-880,75	20487,05

Подставляя значения из этих таблиц в формулы , полу­чим оценки остальных показателей вариации для диаметров и высот:

Диаметры:

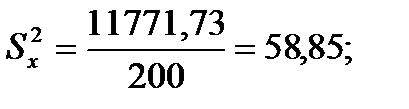
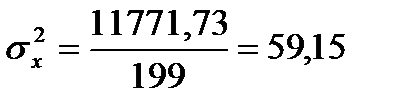
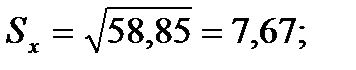
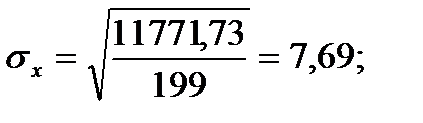
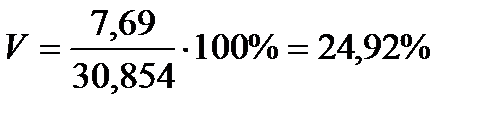
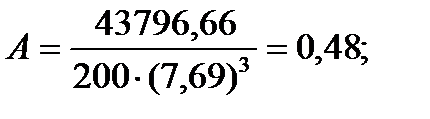
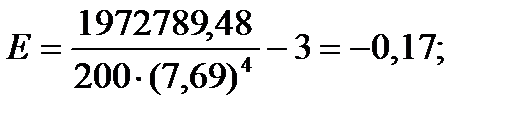
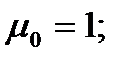
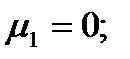
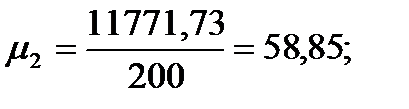
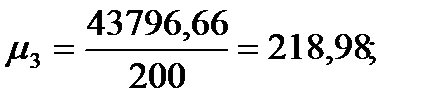
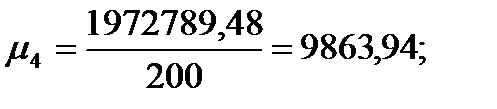
Высоты

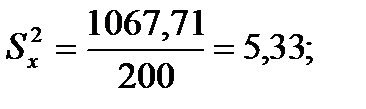
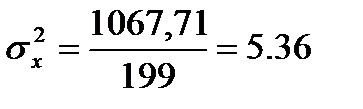
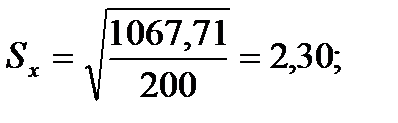
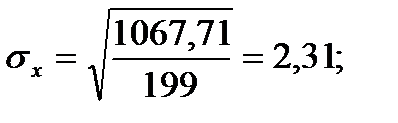
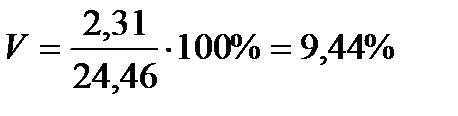
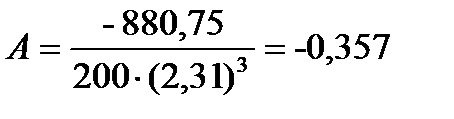
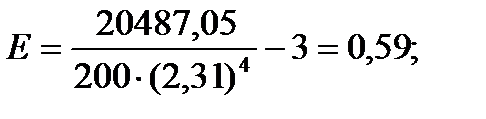
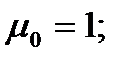
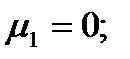
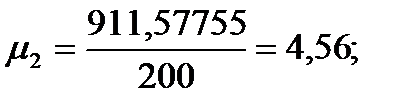
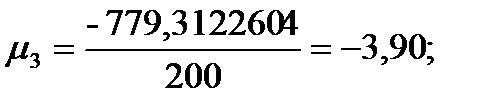
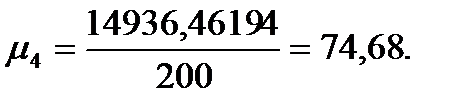
Для того чтобы определить точность полученных оценок стати­стических показателей, вычислим их стандартные ошибки:

Диаметры: Высоты:

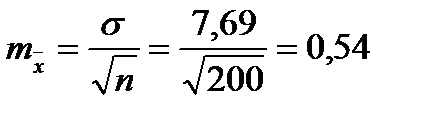
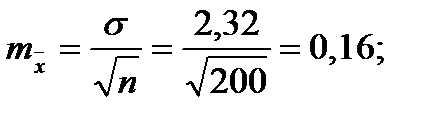
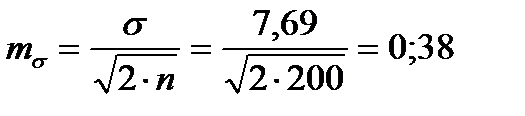
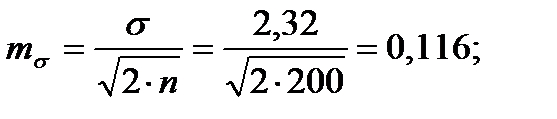
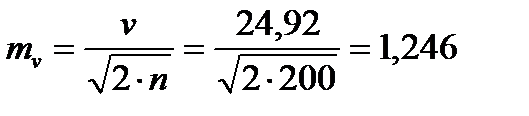
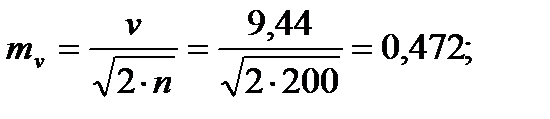
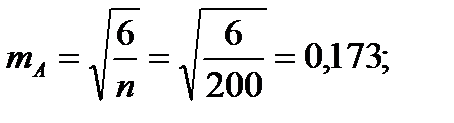
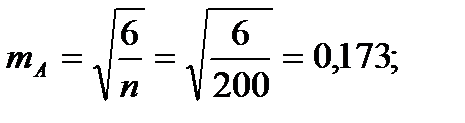
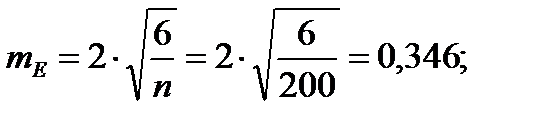
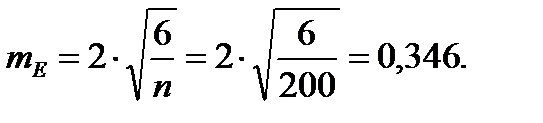
Чтобы сравнивать точность оценки среднего для объектов, имеющих разную размерность, часто используют показатель точно­сти, который представляет собой стандартную ошибку оценки средне­го, выраженную в процентах от самой средней величины. Вычислим показатель точности для рассматриваемого примера:

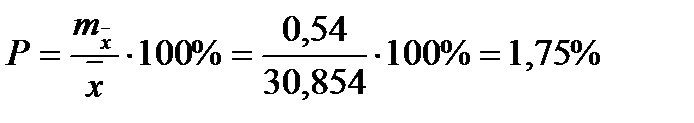-диаметры;

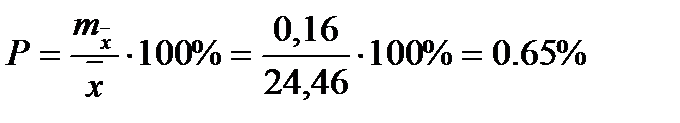-высоты.

Нормальное распределение

Нормальное распределение имеет важное значение в биометрии. На практике очень часто исследуемые случайные величины следуют этому закону. Для того чтобы узнать, подчиняется случайная величи­на закону нормального распределения или нет, надо вычислить теоре­тические частоты вариационного ряда исходя из предположения о нормальном распределении анализируемого параметра и сравнить их с эмпирическими частотами.

Закон распределения случайной величины может быть описан с помощью функции, определяемой соотношением

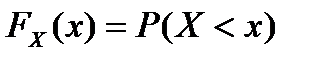
и называемой функцией распределения величины X.

Разность F(b)-F(a) представляет собой вероятность того, что случайная величина X примет значение, принадлежащее интервалу а 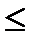X <b, т. е. если а и b являются нижней и верхней границами ин­тервала вариационного ряда, то вероятность попадания изучаемой случайной величины в данный интервал можно вычислить так:

P_a,b=P(a 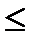X<b)=F(b)-F(a) (1)

Зная эту величину, нетрудно вычислить теоретическое число наблюдений для данного интервала f_a,b=n-P_a,b.

Функция нормального распределения F(x) имеет вид

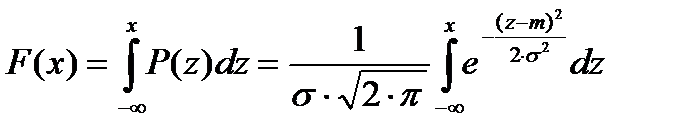(2)

С учетом функции нормального распределения (2) выражение (1) можно переписать следующим образом:

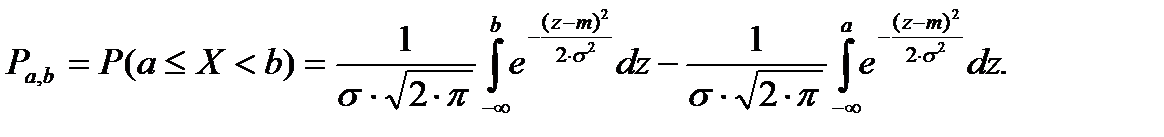(3)

Интегралы, входящие в это выражение, нельзя выразить через элементарные функции, но их можно вычислить через специальную функцию:

,

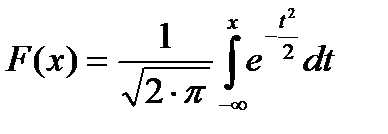которая является интегральной функцией нормального распределения с параметрами т = 0 и σ = 1. Для этого следует перейти к нормиро­ванной случайной величине:

.

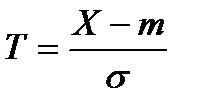Преобразовав неравенство а 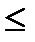Х<b соответствующим обра­зом, получим

.

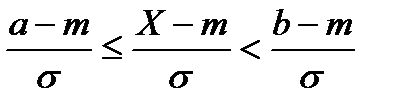Эти два неравенства равносильны, следовательно, их вероятно­сти равны между собой:

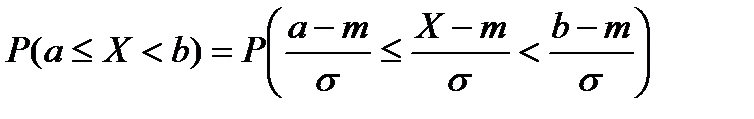. (4)

Используя (3) и (4), получим

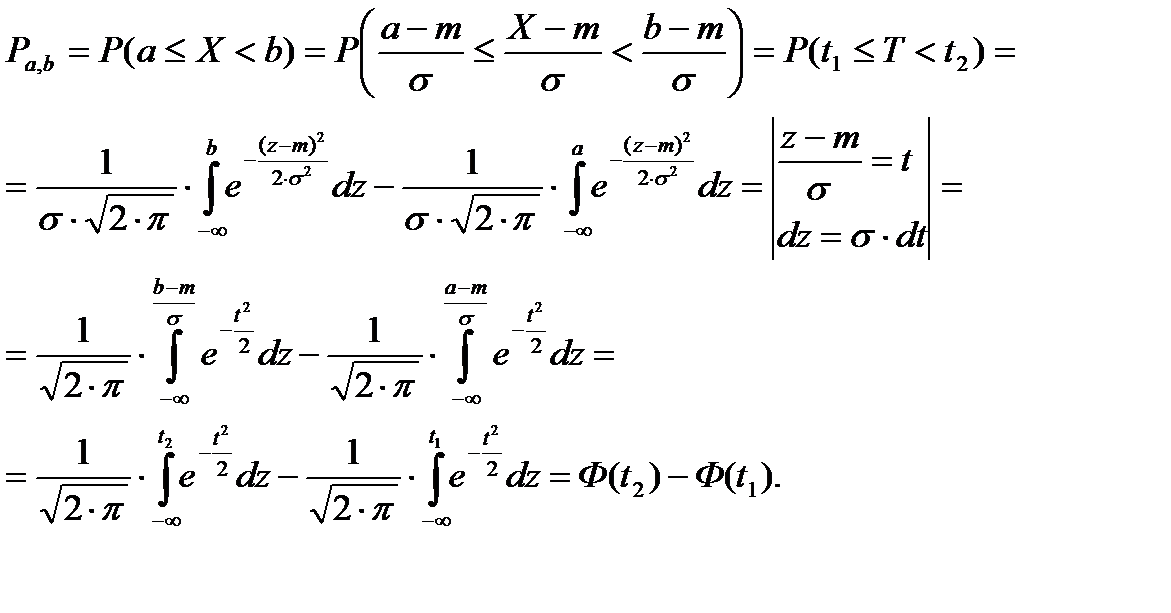(5)

С помощью (5) и данных табл. 2 прил. мы можем вычислить теоретические частоты вариационного ряда, предполагая, что исследуемая случайная величина распределена по нормальному закону.

Выполним эту работу для вариационных рядов по диаметру и высоте. С учетом того, что оценкой параметров нормального распределения методом моментов являются среднеквадратическое отклонение и среднее арифметическое, вычислим нормированные нижнюю и верхнюю границы интервалов следующим образом:

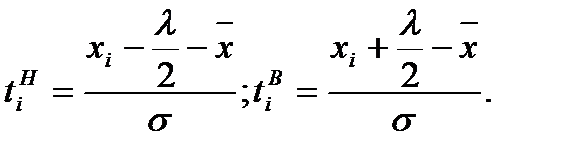
Таблица 10 ─ Вычисление теоретических частот для функции нормального распределения (диаметры).

xi		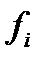tiн	tiв	Ф(tiн)	Ф(tiв)	Рi		∆ -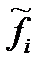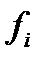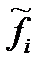
12,7		-∞	-2,17		0,015	0,015	3,	-3,0
15,6		-2,17	-1,79	0,015	0,037	0,022	4,4	-1,4
18,5		-1,79	-1,42	0,037	0,078	0,041	8,2	-1,2
21,4		-1,42	-1,04	0,078	0,149	0,071	14,2	3,8
24,3		-1,04	-0,66	0,149	0,255	0,106	21,2	5,8
27,2		-0,66	-0,29	0,255	0,386	0,131	26,2	5,8
30,1		-0,29	0,09	0,386	0,536	0,15	30,0	1,0
33,0		0,09	0,47	0,536	0,681	0,145	29,0	-10,0
35,9		0,47	0,84	0,681	0,8	0,119	23,8	0,2
38,8		0,84	1,22	0,8	0,889	0,089	17,8	0,2
41,7		1,22	1,6	0,889	0,945	0,056	11,2	-5,2
44,6		1,6	1,98	0,945	0,976	0,031	6,2	-2,2
47,5		1,98	2,35	0,976	0,991	0,015	3,0	4,0
50,4		2,35	2,73	0,991	0,997	0,006	1,2	2,8
53,3		2,73	+∞	0,997	1,000	0,003	0,6	-0,6
Сумма

В отличие от анализируемого вариационного ряда, нормальное распределение определено на интервале от -∞ до +∞. Для того чтобы области определения эмпирического и нормального распределения сделать одинаковыми, добавим дополнительные интервалы перед первым интервалом с границами от -∞ до нижней границы первого интервала и после последнего интервала с границами от верхней гра­ницы последнего интервала до +∞.Эмпирические частоты этих до­полнительных интервалов будут равны нулю, так как в исходных данных нет ни одного наблюдения, которое было бы меньше нижней границы первого интервала или больше верхней границы последнего интервала. Значения функции нормированного нормального распре­деления для нижней 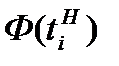и верхней 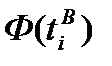границ интервалов можно найти с помощью табл. 2, используя в качестве аргументов значения 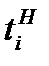и 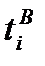соответственно. В этой таблице значения функции распределе­ния даны только для положительных аргументов. Если надо найти функцию распределения для отрицательного аргумента, следует вос­пользоваться соотношением Ф(-х)=1-Ф(х), которое справедливо, так как нормальное распределение является симметричным.

Вероятности для интервалов вариационного ряда легко вычис­лить как разность значений функции распределения для верхней и нижней границ:

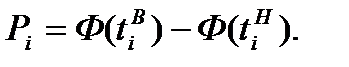
Теперь можно найти теоретические частоты ряда:

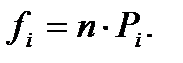
Аналогичным образом можно вычислить теоретические частоты для вариационного ряда высот (табл. 13.).

Последние колонки табл. 12 и 13, представляющие собой раз­ность между эмпирическими и теоретическими частотами, дают нам информацию о близости теоретического (в данном случае нормально­го) и эмпирического распределений. Однако по данным отклонениям достаточно трудно принять решение о согласованности эмпирического и теоретического распределений. Более наглядную картину можно увидеть, изобразив эти распределения графически (рис. 8 и 9). Однако такие сравнения распределений будут субъективными. Для того что­бы дать объективную оценку согласованности эмпирических и теоре­тических распределений, необходимо воспользоваться специальными методиками проверки статистических гипотез.

Корреляционный анализ

В предыдущих разделах высоты и диаметры анализировались по отдельности, вне связи друг с другом. Однако в природе многие случайные величины в той или иной степени связаны друг с другом. Для того чтобы оценить тесноту связи между случайными величина­ми, удобно использовать коэффициент корреляции. Его можно вы­числить по формуле

(8)

Данный показатель оценивает тесноту связи между случайными величинами в случае линейных зависимостей, однако в природе чаще встречаются нелинейные. В таких случаях коэффициент корреляции не может выразить всю полноту связи. Для нелинейных зависимостей лучше использовать показатель, предложенный Пирсоном, который называется корреляционным отношением. Он вычисляется как квад­ратный корень из отношения межгрупповой дисперсии зависимой случайной величины к ее общей дисперсии. В данном случае группы формируются в пределах интервалов вариационного ряда независи­мой переменной. Корреляционное отношение можно вычислить с помощью следующей формулы:

(9)

Стандартные ошибки коэффициента корреляции и корреляци­онного отношения можно оценить с помощью выражений:

(10)

и

(11)

По соотношению величины коэффициента корреляции и корреляционного отношения можно сделать вывод о характере связи: прямолинейна она или криволинейна. Чем значительнее корреляционное отношение превышает коэффициент корреляции, тем более криволинейной является эта связь. Для оценки степени криволинейности связи вычисляют меру криволинейности как разницу между квадратами корреляционного отношения и коэффициента корреляции:

(12)

Вычислим рассмотренные выше показатели связи для пары слу­чайных величин - диаметры и высоты деревьев в древостое. Для того, чтобы выполнить вычисления, составим вспомогательную табл. 18. Подставляя значения сумм из данной таблицы в формулы (8) и (9), получим

или

Теперь, пользуясь выражениями (9) и (10), вычислим стан­дартные ошибки коэффициента корреляции и корреляционного отношения

Полученные результаты говорят о том, что между диаметрами и высотами деревьев в древостое существует связь, а тот факт, что корреляционное отношение значительно превышает коэффициент корреляции, показывает нам, что эта зависимость скорее криволинейная, чем прямолинейная. Вычислим, пользуясь формулой (31), меру криволинейности для зависимости высот и диаметров:

Таблица 16 ─ Вспомогательная таблица для вычисления коэффициента корреляции и корреляционного отношения

H\D	15,6	18,5	21,4	24,3	27,2	30,1		35,9	38,8	41,7	44,6	47,5	50,4	Всего	Yi-ȳ
29,4															4,94
28,5															4,04
27,6															3,14
26,7															2,24
25,8															1,34
24,9															0,44
															-0,46
23,1															-1,36
22,2															-2,26
21,3															-3,16
20,4															-4,06
19,5															-4,96
18,6															-5,86
17,7															-6,76
Итого
ȳx	19,20	19,11	21,95	23,37	24,39	24,73	25,04	25,80	26,15	26,55	26,48	26,96	27,15
ȳx-ȳ	-5,26	-5,35	-2,51	-1,09	-0,07	0,27	0,58	1,34	1,69	2,09	2,02	2,50	2,69
fx(ȳx-ȳ)^2	83,00	200,04	113,40	32,28	0,14	2,19	6,44	43,09	51,41	26,21	16,24	43,65	28,94	647,03
xi-X	-15,25	-12,35	-9,45	-6,55	-3,65	-0,75	2,15	5,05	7,95	10,85	13,75	16,65	19,55
	240,645	462,137	426,951	193,356	7,738	-6,18	23,779	162,408	241,839	136,059	110,825	291,042	210,358	2500,957

Регрессионный анализ

В предыдущем разделе было установлено, что между диаметра­ми и высотами деревьев существует связь. Наличие связи между слу­чайными величинами, как правило, ставит перед исследователем сле­дующую задачу - построение модели этой связи. Эта задача чаще всего решается с помощью регрессионного анализа. В данном случае наличие модели, позволяющей оценивать значения высот деревьев в древостое исходя из их диаметра, может оказать большую практиче­скую пользу, так как трудоемкость измерения высоты растущего де­рева значительно выше, чем трудоемкость измерения его диаметра.

Для построения регрессионного уравнения связи используют метод наименьших квадратов, позволяющий оценить коэффициенты уравнения заданного вида таким образом, чтобы сумма квадратов отклонений эмпирических значений зависимой переменной от теоре­тических значений была наименьшей.

Оценка коэффициентов прямой

Для того чтобы получить оценку коэффициентов и уравне­ния прямой линии методом наименьших квадратов, следует решить систему нормальных уравнений:

(10)

Рассмотрим процесс вычисления коэффициентов уравнения прямой, моделирующей зависимость между высотами и диаметрами. Для этого на основе корреляционной решетки (табл. 4) составим вспомогательную таблицу для вычисления всех необходимых сумм (табл. 17). В данной таблице суммы вычисляются сначала по интерва­лам, а затем складываются. Подставив значения сумм в систему нор­мальных уравнений (10), получим

(11)

Решим полученную систему уравнений. Для этого разделим ка­ждое из уравнений системы (12) на коэффициенты при параметре :

(12)

Теперь вычтем первое уравнение системы (14) из второго:

(13)

и выразим из полученного уравнения (15) коэффициент :

(14)

Таблица 17 ─ Вспомогательная таблица для вычисления коэффициента регрессии прямой

H\D	15,6	18,5	21,4	24,3	27,2	30,1		35,9	38,8	41,7	44,6	47,5	50,4	Всего
29,4															58,8
28,5
27,6															331,2
26,7															667,5
25,8
24,9															647,4
23,1															438,9
22,2															355,2
21,3															149,1
20,4
19,5
18,6															55,8
29,4															4821,9
fx	46,8	129,5	385,2	656,1	870,4	933,1	627,0	861,6	698,4	250,2	178,4	332,5	201,6	6170,8
∑fi*xi	730,1	2395,8	8243,3	15943,2	23674,9	28086,3	20691,0	30931,4	27097,9	10433,3	7956,6	15793,8	10160,6	202138,3
∑fi*xi2	898,6	1820,4	8076,4	14900,8	21232,3	23071,7	15701,4	22229,3	18263,2	6642,8	4723,1	8963,3	5473,4	151996,5
∑fij*yj*xi	19,9	20,7	21,5	22,3	23,1	23,9	24,7	25,5	26,3	27,1	27,9	28,7	29,5
y̅i	2,1	10,9	25,8	128,4	143,6	67,0	48,0	31,4	28,1	5,6	8,5	29,9	24,0	553,4
∑fij*(yi-yi˜)2	15,6	18,5	21,4	24,3	27,2	30,1		35,9	38,8	41,7	44,6	47,5	50,4	Всего

Подставляя вычисленное значение коэффициента в первое уравне­ние системы (34) и выразив из него коэффициент , получим

(14)

Таким образом, у нас получилась регрессионная модель зависимости высоты от диаметра деревьев в сосновом древостое следующего вида:

(15)

или, используя другие обозначения:

(16)

Пользуясь полученным регрессионным уравнением прямой ли­нии, определим теоретические высоты и сумму квадратов отклоне­ний эмпирических высот от теоретических (табл. 19). Полученное значение суммы квадратов отклонений 553,4 мы можем использовать для вычисления стандартной ошибки регрессионного уравнения пря­мой:

(17)

На рис. 12 изображено полученное регрессионное уравнение прямой линии.

Введение

Лесная биометрия решает задачи обработки массовых (статистических) данных. Экспериментальные материалы, собранные в лесу, как раз и являются таковыми. Как правило, они представлены в виде числовых значений, характеризующих различные лесные объекты (высота, диаметр или объем дерева; число шишек на дереве; количество семян в шишке и т. д.). В связи с этим предметом лесной биометрии являются различные случайные величины, характеризующие сообщества.

Основная задача лесной биометрии – количественный и качественный анализ массовых случайных явлений, имеющих место в лесных биогеоценозах. Такая процедура подразумевает ряд этапов: организация и планирование наблюдений; сбор экспериментальных данных; свертка информации, т. е. сведения большого количества исходных данных к небольшому числу параметров, которые в сжатом виде характеризуют всю исследуемую совокупность; анализ экспериментальных данных; принятие решен