Исследование точности измерения линейного размера

Проводилось путем возврата проконтролированного изделия в цех и подачи его на контроль повторно с очередной партией изделий. Когда одно и то же изделие было подвергнуто контролю 30 раз через примерно равные промежутки времени, были сделаны выписки из журнала контролера, в котором он регистрировал результаты измерения изделия.

Результаты измерений в мм были выписаны в том порядке, в котором они были получены. Образовался следующий ряд:

№ измерения	Результат измерения	№ измерения	Результат измерения	№ измерения	Результат измерения
	40,15		40,17		40,18
	40,15		40,17		40,19
	40,15		40,17		40,19
	40,17		40,17		40,18
	40,16		40,17		40,21
	40,16		40,15		40,19
	40,16		40,18		40,18
	40,15		40,19		40,19
	40,16		40,18		40,19
	40,16		40,18		40,19

Решение

Первичная обработка последовательности промежуточных измерений одной и той же величины заключается в исключении переменной составляющей систематической погрешности с целью исправления результатов измерений и их группирования для получения вариационного ряда.

Переменная составляющая погрешности измерений должна выявляться, исключаться из результатов измерений и учитываться в оценках систематической погрешности. Она может быть выявлена сложными методами дисперсионного анализа. Однако для решения инженерных задач обычно достаточно применить графический метод. Для этого строится график.

На графике проводят плавную кривую, которая выражает тенденцию изменения результатов измерения. В рассматриваемом примере явно выражена прогрессирующая линейно возрастающая по модулю погрешность. Можно зафиксировать, что модуль переменной составляющей систематической погрешности равняется 0,05 мм. На одно значение , тогда для каждого порядкового номера можно пересчитать , где - порядковый номер измерения. Округлив значение до сотых долей мм, ее исключают из результатов измерений. Получают следующий ряд значений.

№ измерения	Результаты измерений	Ряд значений после исключения переменной составляющей
	40,15	40,15
	40,15	40,15
	40,15	40,15
	40,17	40,16
	40,16	40,15
	40,16	40,15
	40,16	40,15
	40,15	40,14
	40,16	40,15
	40,16	40,14
	40,17	40,15
	40,17	40,15
	40,17	40,15
	40,17	40,15
	40,17	40,15
	40,15	40,12
	40,18	40,15
	40,19	40,16
	40,18	40,15
	40,18	40,15
	40,18	40,15
	40,19	40,15
	40,19	40,15
	40,18	40,14
	40,21	40,17
	40,19	40,15
	40,18	40,13
	40,19	40,14
	40,19	40,14
	40,19	40,14

Сгруппировав исправленные результаты, получают следующий вариационный ряд:

Результаты измерений	40,12	40,13	40,14	40,15	40,16	40,17
Число результатов

Пример 1

Для изучения случайной погрешности нестандартизованного СИ температуры, этим средством в соответствии с инструкцией по эксплуатации через равные промежутки времени многократно была измерена температура тела настолько большой массы, что изменение ее температуры за все время измерения пренебрежимо мало.

№ измерения	Результат измерения,	№ измерения	Результат измерения,
	40,40		40,79
	40,43		40,76
	40,49		40,76
	40,57		40,76
	40,57		40,72
	40,59		40,73
	40,69		40,71
	40,70		40,69
	40,68		40,68
	40,68		40,75
	40,68		40,71
	40,66		40,63
	40,68		40,63
	40,78		40,58
	40,73		40,56
	40,73		40,64
	40,76		40,58
	40,79		40,58
	40,76		40,57
	40,80		40,46

№ измерения	Результаты измерений температуры	Ряд значений после исключения переменной составляющей
	40,40	40,40
	40,43	40,38
	40,49	40,40
	40,57	40,44
	40,57	40,41
	40,59	40,40
	40,69	40,47
	40,70	40,46
	40,68	40,42
	40,68	40,40
	40,68	40,38
	40,66	40,35
	40,68	40,36
	40,78	40,44
	40,73	40,38
	40,73	40,37
	40,76	40,40
	40,79	40,42
	40,76	40,38
	40,80	40,42
	40,79	40,41
	40,76	40,38
	40,76	40,38
	40,76	40,39
	40,72	40,35
	40,73	40,37
	40,71	40,36
	40,69	40,35
	40,68	40,36
	40,75	40,44
	40,71	40,42
	40,63	40,35
	40,63	40,37
	40,58	40,34
	40,56	40,34
	40,64	40,44
	40,58	40,40
	40,58	40,42
	40,57	40,44
	40,46	40,36

Строим вариационный ряд:

Значение	Условное обозначение количества	Цифровое обозначение количества
40,34
40,35
40,36
40,37
40,38
40,39
40,40
40,41
40,42
40,43	-	-
40,44
40,45	-	-
40,46
40,47

Среднее значение

Среднеквадратическое отклонение:

или

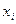	40,34		-7		-14
	40,35		-6		-24
	40,36		-5		-20
	40,37		-4		-12
	40,38		-3		-18
	40,39		-2		-2
	40,40		-1		-6
	40,41
	40,42
	40,43	-			-	-
	40,44
	40,45	-			-	-
	40,46
	40,47

Пример 2

На ряде образцов был измерен момент в килограммометрах, требуемый для запирания коробки радиопередатчика. Результаты измерения приведены в таблице.

	0,62		0,64		0,46		0,48		0,66
	0,40		0,58		0,60		0,66		0,67
	0,60		0,80		0,75		0,52		0,67
	0,53		0,60		0,51		0,58		0,70
	0,45		0,57		0,70		0,73		0,58
	0,65		0,60		0,75		0,73		0,60
	0,59		0,70		0,55		0,57		0,50
	0,70		0,60		0,60		0,55		0,50
	0,60		0,60		0,55		0,65		0,80
	0,60		0,60		0,42		0,60		0,50

Вычислить среднее арифметическое, выборочную дисперсию.

Решение

1. Округлим количество интервалов по формуле Старджесса

2. Вычисляем ширину интервалов

3. Определим границы интервалов, частоту попадания в интервалы и середины интервалов.

№ инт.	Границы интервалов	Середины интервалов	Частота попадания в интервалы	Статистическая вероятность (частость)
	0,37…0,43	0,40		0,04	-3	-6
	0,43…0,49	0,46		0,06	-2	-6
	0,49…0,55	0,52		0,12	-1	-6
	0,55…0,61	0,58		0,42
	0,61…0,67	0,64		0,12
	0,67…0,73	0,70		0,12
	0,73…0,79	0,76		0,08
	0,79…0,85	0,82		0,04

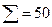4. Вычислим среднее арифметическое и СКО

или