Тема 2. Элементы дискретной математики.
Множества. Задание множеств. Конечные и бесконечные множества. Подмножество. Операции над множествами. Дополнение множеств. Эквивалентность множеств. Мощность множеств.
Комбинаторика. Выборки. Основные правила комбинаторики. Выборки без повторений. Выборки с повторениями. Сочетания. Размещения. Перестановки.
Тема 3. Основные понятия теории вероятностей и математической статистики.
Случайные события, их классификация. Классическое определение вероятности. Статистическое определение вероятности. Действия над событиями. Вероятность суммы и произведения событий. Условная вероятность. Повторные независимые испытания. Формула Бернулли.
Дискретные случайные величины, законы распределения, числовые характеристики: математическое ожидание, дисперсия, среднее квадратическое отклонение. Непрерывные случайные величины, законы распределения, числовые характеристики. Равномерное, показательное, нормальное распределения. Распределение Бернулли (биномиальное) и Пуассона.
Статистические методы обработки экспериментальных данных. Случайная выборка из генеральной совокупности, ее табличное и графическое представление. Способы отбора: собственно-случайный (повторный и бесповторный), механический, типический, серийный.
ПЛАНЫ ПРАКТИЧЕСКИХ ЗАНЯТИЙ
Тема 1. Элементы линейной алгебры
Практическое занятие №1.Матрицы. Действия над матрицами. Вычисление определителей второго и третьего порядков.
Практическое занятие №2.Алгебраические дополнения и миноры. Вычисление определителя разложением по строке (столбцу).
Практическое занятие № 3. Решение систем 2-х (3-х) линейных уравнений с 2-мя (3-мя) неизвестными методом Крамера.
Практическое занятие №4.Обратная матрица. Алгоритм нахождения обратной матрицы. Решение 2-х (3-х) линейных уравнений с 2-мя (3-мя) неизвестными матричным методом
Практическое занятие №5.Ранг матрицы. Система m линейных уравнений с n неизвестными. Метод Гаусса. Теорема Кронекера – Капелли.
Практическое занятие №6. Контрольная работа.
Литература[1]
Основная
1. Информатика и математика для юристов: Учебник для студентов вузов, обучающихся по юридическим специальностям / С.Я. Казанцев, В.Н. Калинина, О.Э. Згадзай; Под ред. С.Я. Казанцев, Н.М. Дубинина. - 2-e изд., перераб. и доп. – Изд.:ЮНИТИ-ДАНА, 2010. 560с.*
Дополнительная
1. Математика для юридических специальностей: Учебное пособие для студ. учреждений высш. проф. образования / С.Я. Казанцев, О.Э. Згадзай, Н.Х. Сафиуллин. - (Университетский учебник ; Высшая математика и ее приложения к юриспруденции. –ИЦ: Академия , 2011. –224с.
Тема 2. Элементы дискретной математики.
Практическое занятие №7.Множества и действия над ними.
Практическое занятие №8.Элементы комбинаторики. Основные правила комбинаторики. Выборки без повторений. Выборки с повторениями. Сочетания. Размещения. Перестановки.
Литература
Основная
1. Математика для юридических специальностей: Учебное пособие для студ. учреждений высш. проф. образования / С.Я. Казанцев, О.Э. Згадзай, Н.Х. Сафиуллин. - (Университетский учебник ; Высшая математика и ее приложения к юриспруденции. –ИЦ: Академия , 2011. –224с.
2. Информатика и математика для юристов: Учебник для студентов вузов, обучающихся по юридическим специальностям / С.Я. Казанцев, В.Н. Калинина, О.Э. Згадзай; Под ред. С.Я. Казанцев, Н.М. Дубинина. - 2-e изд., перераб. и доп. – Изд.:ЮНИТИ-ДАНА, 2010. 560с.*
Дополнительная
1. Малыхин В.И. Высшая математика.2-е изд. Гриф УМО МО РФ. Инфра-М, 2010г. –365с.
2. Красс М.С. Чупрынов Б.П. Математика для экономического бакалавриата. Учебник.– Инфра-М, 2011г. –472с.
3. Гмурман В.Е.ТЕОРИЯ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА 12-е изд. Учебное пособие для бакалавров М.:Издательство Юрайт, 2012г.– 479с.
4. ТЕОРИЯ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА. Учебник для бакалавров / А.М.Попов, В.Н.Сотников . М.:Издательство Юрайт, 2011г.–440с.
Тема 3. Основные понятия теории вероятностей и математической статистики.
Практическое занятие №9.Основные понятия теории вероятности.Классическое определение вероятности. Статистическое определение вероятности. Действия над событиями.
Случайные величины, законы распределения, числовые характеристики: математическое ожидание, дисперсия, среднее квадратическое отклонение.
Основные понятия математической статистики. Статистические методы обработки экспериментальных данных.
Практическое занятие №10.Контрольная работа.
Литература
Основная
1. Математика для юридических специальностей: Учебное пособие для студ. учреждений высш. проф. образования / С.Я. Казанцев, О.Э. Згадзай, Н.Х. Сафиуллин. - (Университетский учебник ; Высшая математика и ее приложения к юриспруденции. –ИЦ: Академия , 2011. –224с.
2. Информатика и математика для юристов: Учебник для студентов вузов, обучающихся по юридическим специальностям / С.Я. Казанцев, В.Н. Калинина, О.Э. Згадзай; Под ред. С.Я. Казанцев, Н.М. Дубинина. - 2-e изд., перераб. и доп. – Изд.:ЮНИТИ-ДАНА, 2010. 560с.*
Дополнительная
1. Красс М.С. Чупрынов Б.П. Математика для экономического бакалавриата. Учебник.– Инфра-М, 2011г. –472с.
2. Гмурман В.Е.ТЕОРИЯ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА 12-е изд. Учебное пособие для бакалавров М.:Издательство Юрайт , 2012г.– 479с.
3. ТЕОРИЯ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА. Учебник для бакалавров / А.М.Попов, В.Н.Сотников . М.:Издательство Юрайт, 2011г.–440с.
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ПО ИЗУЧЕНИЮ ДИСЦИПЛИНЫ И ПО ОРГАНИЗАЦИИ САМОСТОЯТЕЛЬНОЙ РАБОТЫ СТУДЕНТОВ
Преподаватель так должен строить свое изложение материала, чтобы сформировать у студентов целостное восприятие курса, чтобы при изучении математики обучаемый видел логическую взаимозависимость тем курса, наглядно видел необходимость применение математических формул, расчетов понятий в своей профессиональной деятельности. Тем самым преподаватель повышаетмотивацию в изучении предмета, а успешное усвоение курса повышает самооценку студента, стимулирует на новые успехи в учебе.
На практических занятиях следует отрабатывать основные методы решения типовых задач. Практическое занятие проводить с использованием учебно-методических пособий, выполненных преподавателями кафедры, где подобраны типовые задания по данному разделу и приведены задачи для самостоятельного решения, адаптированные к требованиям учебной программы вуза.
При контроле знаний основное внимание уделяется способности студентов применять полученные знания на практических задачах. Поэтому при самостоятельной работе студент должен уделять внимание решению задач. При решении задач необходимо анализировать те или иные алгоритмы, которые применялись при решении подобных задач на аудиторных занятиях, пытаться построить логическую схему доказательства. Если задача сразу не получается, то отложить ее на некоторое время, рассмотреть другие задачи, но обязательно вернуться и попытаться решить отложенную задачу попозже. Материал раздела курса можно усвоить только прорешав достаточный по объему набор задач по данному разделу. При чтении теоретического материала необходимо попытаться вникнуть в содержание определений, попробовать построить собственные примеры на данное определение. Необходимо уметь связывать различные определения и понятия в одно целое.
В разделе теория вероятностей необходимо обратить внимание на две модели построения вероятностных схем: классическую и аксиоматическую (по Колмогорову). При решении задач на вычисление вероятностей основное внимание уделяется комбинаторным методам подсчета числа вариантов выбора множеств, определяемых условиями задачи. Кроме того, необходимо понимать формулу полной вероятности и формулу Байеса.
Организация самостоятельной работы студентов имеет цель:
— систематизировать и расширить их теоретические знания;
— закрепить практические и организаторские способности;
— научить работать с учебной и научной литературой;
— стимулировать профессиональный рост студентов, воспитывать творческую активность и инициативу.
Самостоятельная работа студентов организуется преподавателями в соответствии с календарным планом изучения дисциплины и предполагает:
— изучение лекционного материала, чтение рекомендуемых литературных источников, решение задач, ответы на контрольные вопросы или тесты и т.д.,
— самостоятельное изучение материала по заданным преподавателем темам;
— самостоятельное выполнение индивидуальных заданий;
— написание контрольной работы.
Самостоятельная работа представляет собой дополнительное изучение дисциплины для полного и глубокого усвоения материала на основе анализа учебной, методической и дополнительной литературы.
Самостоятельная работа студентов включает повторение пройденного материала и подготовку к контрольной работе. Вся самостоятельная работа студентов оценивается в течение семестра на практических занятиях.
Повторение пройденного материала осуществляется в процессе выполнения домашнего задания и самостоятельной проработки теоретического материала.
ЗАДАНИЯ ДЛЯ ВЫПОЛНЕНИЯ КОНТРОЛЬНЫХ РАБОТ
Контрольная работа№1
1. Даны матрицы 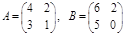
Найти их сумму 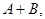 произведение AB и разность A - B.
произведение AB и разность A - B.
2. Записать систему в матричной форме 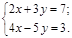
3. Вычислить определитель 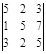 .
.
4. Решить систему с помощью метода Крамера и метода Гаусса.
а) 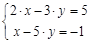 б)
б) 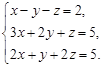
Контрольная работа№2
1. Найти АÈВ, АÇВ, А/В, В/А, если А и В следующие:
А={2, 3, 4, 5}, B={5, 6, 7, 8}
2. 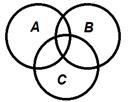 Заштриховать ту часть диаграммы, которая соответствует следующему множеству:
Заштриховать ту часть диаграммы, которая соответствует следующему множеству:
a) (A∪B)\(C∩B);
b) (A\B)∩(C\B);
c) (C\A)∪(C\B);
d) (C\A)∩(C\B);
e) (C\B)∪(A\C);
f) (A∩C)∆(B∪A)\C.
2. В правлении акционерного общества 20 человек. Необходимо избрать председателя правления, его заместителя и казначея. Сколькими способами можно образовать эту руководящую тройку, если одно лицо может занимать только один пост?
3. Сколько разных буквосочетаний можно образовать при перестановке букв следующего слова: ЮРИСТ?
4. В магазине имеются фрукты 4 видов. Сколькими способами можно сформировать подарочный набор к празднику пожилого человека из 3 фруктов?
5. Сколько разных 3-значных чисел можно составить их следующих цифр 1, 2, 3, 4 при условии, что ни одна цифра не повторяется?
6. Для работы с инвалидами группе социальных работников необходимо командировать 5 сотрудников. Сколькими способами это можно сделать, если весь штат составляет 12 человек?
7.Сколько телефонных номеров можно составить при условии, что первые две цифры 4 и 2, всего цифр в номере 7?
8.Бросают две игральные кости. Найти вероятность того, что сумма выпавших цифр будет
9.а) = 9, б) < 10.
10. Из колоды в 32 карты наугад вынимают одну за другой вынимают 2 карты. Найти вероятность того, что:
а) вынуты 2 короля
б) вынуты 2 карты пиковой масти
в) вынуты валет и дама
11. В цехе 20 станков. Для любого станка вероятность того, что он останется исправным в течении месяца, равна 0,8. Какова вероятность того, что:
а) в течении месяца хотя бы один станок выйдет из строя
б) в течении месяца выйдет из строя ровно 2 станка.
12. В трех группах учатся соответственно 12,15 и 21 студентов. По теории вероятностей (ТВ) получили отличные оценки 6 студентов первой группы, 4 – второй, 2 – третьей. Наугад выбирается студент. Найти вероятность того, что выбранный студент получил по ТВ отличную оценку.
13. На вступительных экзаменах по математике тридцать абитуриентов набрали баллы: 7,10, 8, 7, 6, 8,9, 9, 6, 7, 7, 8, 8, 9, 10, 8, 9, 8, 7, 7, 6, 8, 9, 7, 8, 8, 7, 9, 10, 9. По полученным результатам:
‑ составить статистический ряд;
‑ построить полигон относительных частот;
‑ найти точечные оценки 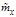 ,
, 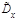 ,
, 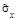 ;
;
‑ построить доверительный интервал для 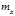 с заданной доверительной вероятностью
с заданной доверительной вероятностью 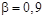 .
.
ПРИМЕРЫ ТЕСТОВЫХ ЗАДАНИЙ ДЛЯ ПРОВЕДЕНИЯ ПРОМЕЖУТОЧНОЙ АТТЕСТАЦИИ
