Тема: Численные методы в математическом моделировании теплотехнических задач и их программная реализация. Методы интерполирования.

План: Элементы численных методов и их компьютерная реализация. Приближение функций.Интерполирование, полиномиальное интерполирование, интерполирование сплайнами, аппроксимация кривыми при решении задач приближения функций и расчета теплотехнических таблиц.

В настоящее время численные методы являются мощным математическим средством решения научно-технических задач и проблем. Это связано с тем, что в большинстве случаев невозможно получить точное аналитическое решение, а также со стремительным развитием компьютерной техники. Существует множество стандартных программ и объектно- ориентированных пакетов прикладных программ (ППП). Однако научным и инженерным работникам необходимо понимать сущность основных численных методов и алгоритмов, поскольку интерпретация результатов вычислительного эксперимента нетривиальна и требует специальных знаний особенностей применяемых методов.

Численный анализ является завершающей составляющей математической подготовки теплоэнергетика. Знание основ теории и способов реализации численных методов необходимо при проектной проработке и расчетном обосновании процессов, установок, агрегатов, систем теплоэнергетики и теплотехнологии.

Вы познакомитесь с методами аппроксимации функций, численного решения алгебраических и трансцендентных уравнений, а также систем линейных и нелинейных уравнений, задачами численного интегрирования и дифференцирования, методами решения обыкновенных дифференциальных уравнений, кратким введением в методы решения дифференциальных уравнений в частных производных и задач оптимизации. Практически все методы иллюстрируются алгоритмами и примерами их применения при решении теплотехнических задач. Рассматриваются вопросы реализации изучаемых численных методов на персональном компьютере (РС) с применением программных математических пакетов, которые широко используются в практических вычислениях. Закрепление теоретических знаний достигается при выполнении лабораторного практикума по дисциплине.

Интерполирование функций

Интерполяция применяется во многих задачах, связанных с вычислениями. Укажем некоторые из этих задач.

Обработка физического эксперимента – построение приближенных формул для характерных величин по табличным данным, полученным экспериментально.

Построение приближенных формул по данным вычислительного эксперимента. Здесь возникают нестандартные задачи интерполяции, так как обычно записываются формулы, с возможно более простой структурой.

Субтабулирование - сгущение таблиц применяется в тех случаях, когда непосредственное вычисление функций трудно или когда имеется мало экспериментальных данных. В РС вводится небольшая таблица, а нужные при расчетах значения функции находятся по мере необходимости по интерполяционной формуле.

Интерполяция применяется также в задаче обратного интерполирования: задана таблица у_i = y(x_i); найти х_i как функцию от у_i. Примером обратного интерполирования может служить задача о нахождении корней уравнения.

Интерполяционные формулы используются также при вычислении интегралов, при написании разностных аппроксимаций для дифференциальных уравнений на основе интегральных тождеств.

В общем случае при постановке задачи приближения нужно следовать по алгоритму:

- определить какой класс приближенных функций нужно выбрать;

- выбрать критерий близости («согласия») исходной и приближающей функции (совпадение в узловых точках – метод Лагранжа, или метод наименьших квадратов);

- указать правило, позволяющее с заданной степенью точности, получить значение функции в промежуточных точках между узлами (какие узлы использовать и как их расположить).

Часто требуется восстановить функцию f(x) для всех значений х на отрезке а ≤ х ≤ b, если известны ее значения в некотором конечном числе точек этого отрезка. Эти значения могут быть найдены в результате наблюдений (измерений) в каком-то натурном эксперименте, либо в результате вычислений. Кроме того, может оказаться, что функция f(x) задается формулой и вычисления ее значений по этой формуле очень трудоемки, поэтому желательно иметь для функции более простую (менее трудоемкую для вычислений) формулу, которая позволяла бы находить приближенное значение рассматриваемой функции с требуемой точностью в любой точке отрезка. В результате возникает следующая математическая задача.

Пусть на отрезке а £ x £ b задана сетка ω ={х₀ = а < х₁ <¼< х_n = b } и в ее узлах заданы значения функции у (х), равные у (х₀) = у₀, …, у(х_i) = у_i, …, у(х_n) = у_n. Требуется построить интерполянту– функцию f(х), совпадающую с функцией у(х) в узлах сетки:

f (x_i) = y_i, i = 0, 1, …, n (3.1)

Основная цель интерполяции – получить быстрый (экономичный) алгоритм вычисления значений f(x) для значений х, не содержащихся в таблице данных.

Основной вопрос: как выбрать функцию - интерполянту f(х) и оценить погрешность у(х) - f(х)?

Интерполирующие функции f(х), как правило, строятся в виде линейных комбинаций некоторых элементарных функций:

f(x) = ,

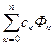
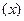где {Ф 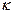(х)} - фиксированные линейно независимые функции;

с₀, с₁, …, с_n - не определенные пока коэффициенты.

Из условий (3.1) получим систему n+1 уравнений относительно коэффициентов {с }: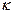

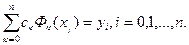
Предположим, что система функций Ф 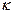(х) такова, что при любом выборе узлов а = х₀< х₁ < …< х_n = b отличен от нуля определитель системы:

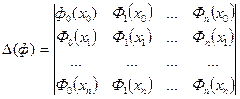
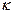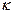Тогда по заданным у_i (i = 0,1,…, n ) однозначно определяются коэффициенты с ( = 0, 1, …, n).

В качестве системы линейно независимых функций {Ф 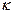(х)} чаще всего выбирают: степенные функции Ф 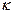(х) = х 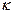(в этом случае f = P_n (x) – полином степени n ); тригонометрические функции { Ф 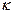(х) = соs kх, sin kx} (в этом случае f - полином тригонометрический). Используются также рациональные функции

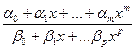
и другие виды интерполирующих функций.

Рассмотрим полиномиальную интерполяцию.

Известно, что любая непрерывная на отрезке [а, b] функция f(x) может быть хорошо приближена некоторым полиномом Р_n(х).

Будем искать интерполяционный полиномв виде

Р_n(x) = 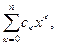( 3.2 )

где с 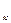- неопределенные пока коэффициенты.

Полагая f (x_i) = y_i, получим систему линейных уравнений вида

с₀+с₁ х₀+…+с_nх₀ⁿ= y₀,

с₀+с₁ х₁+…+с_nх₁ⁿ= y₁,

…………………..…,

с₀+с₁ х_n+…+с_nх_nⁿ= y_n.

Определитель этой системы отличен от нуля, т.е. полином вида (3.2) существует и единственен. Форм записей такого полинома существует множество.

В качестве базиса {Ф 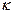(х)} мы взяли базис из одночленов 1, х, х², …, хⁿ. Для вычислений более удобным является базис полиномов Лагранжа {l 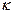(x)} степени n или коэффициентов Лагранжа:

l 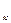(x_i) = 1, если i = k,

0, если i ≠ k , i, k = 0, 1, …, n.

Нетрудно видеть, что полином степени n

l 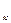(x) = l 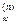(x) =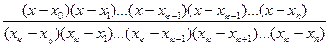

удовлетворяет этим условиям. Полином l 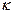(x), очевидно, определяется единственным образом.

Полином l 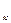(x) y 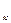принимает значение у 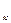в точке х 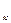и равен нулю во всех остальных узлах х 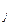при j ¹ k. Отсюда следует, что интерполяционный полином

Р_n(x) = 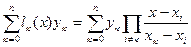(3.3)

имеет степень не выше n и Р_n (x_i) = y_i. Формулу (3.3) называют формулой Лагранжа. К достоинствам формулы можно отнести то, что число арифметических действий для вычисления пропорционально n².

Для оценки близости полинома Р_n(х) к функции f(х) предполагают, что существует (n+1)-я непрерывная производная f⁽ⁿ⁺¹⁾ (х).