Тема: Математическое и физическое моделирование в теплоэнергетике. Процесс разработки и использования математических моделей.

План:Основные понятия математического и физического моделирования. Аналоговое моделирование. Процесс разработки и использования математических моделей. Методы и средства ускорения моделирования. Использование системного анализа при моделировании.

В дальнейшем будем рассматривать физическое моделированиеи аналоговое -из предметного, математическое моделирование-из знакового.

Введем ряд определений.

Математическая модель –приближенное описание какого-либо класса явлений внешнего мира, выраженное с помощью математической символики.

Математическое моделирование - процесс изучения явления с помощью математической модели.

Процесс математического моделирования можно подразделить на четыре этапа:

первый - формулирование законов, связывающих основные объекты модели, результат - запись в математических терминах сформулированных качественных представлений о связях между объектами модели;

второй – исследование математических задач, к которым приводят математические модели, основной вопрос – решение прямой задачи – получение в результате анализа модели выходных данных (теоретических следствий) для сопоставления их с результатами наблюдений изучаемых явлений;

третий - выяснение того соответствует ли принятая модель (гипотетичная) критерию практики, т.е. выяснение вопроса о том, согласуется ли результат наблюдений с теоретическими следствиями модели в пределах точности наблюдений. Задачи, в которых определяются характеристики модели таким образом, чтобы выходная информация была сопоставима в пределах точности наблюдений с результатами наблюдений – обратная задача;

четвертый – последующий анализ модели в связи с накоплением данных об изучаемых явлениях и модернизация модели.

Метод математического моделирования занимает ведущее место среди других методов исследования.

Физическое моделирование –экспериментальный метод научного исследования, состоящий в замене изучаемого физического процесса, явления или объекта другим, ему подобным – моделью. Геометрически подобная оригиналу модель имеет увеличенный или уменьшенный по сравнению с оригиналом размер. Модель может отличаться от реального процесса или явления количественными физическими характеристиками.

В основе физического моделирования лежит теория подобия и анализ размерностей.

Кроме прямого физического моделирования при исследовании различных физических процессов используются различные аналогии, позволяющие на основе однотипности математических уравнений, описывающих различные физические процессы, заменять изучение исследуемого процесса изучением другого процесса.

Например, при моделировании процессов теплообмена используется электротепловая аналогия, в которой исследуемое поле температур заменяется полем электрического потенциала в контуре CR (С- электрическая емкость, R-омическое сопротивление) .

При физическом моделировании сохраняется физическая природа исследуемого объекта. В случае моделирования аналогиями модель воспроизводит иное физическое явление, отличное по своей природе от натурного, но описываемого теми же уравнениями. Метод аналогий основан на формальной идентичности дифференциальных уравнений, описывающих различные по своей физической природе процессы (проявление единства природы).

На существование электрогидродинамической аналогии (ЭГДА) указывал еще Г.Кирхгоф в 1845 г. Метод ЭГДА основан на аналогии уравнений движения электрическоготока и уравнений потенциального течения жидкости. Метод магнитогазодинамической аналогии (МАГА) использует аналогию между уравнениями магнитного поля и уравнениями потенциального течения газа. Газогидравлическая аналогия (ГГА) основана на аналогии между уравнениями движения невязкой несжимаемой жидкости в открытом канале и уравнениями плоского потенциального движения газа. Ни один из указанных методов аналогий не позволяет моделировать силы вязкости. Электротепловая аналогия основана на замене поля температурполем электрического потенциала в CRконтуре, аналогом коэффициента температуропроводности является величина 1/CR. Гидротепловая аналогия дает возможность моделирования процессов стационарной теплопроводности на аналогии с безвихревым потоком идеальной жидкости.

Начало практическому применению метода ЭГДА к решению задач, связанных с движением жидкости было положено Д.Тома, который применил метод ЭГДА при изучении движения воды в направляющем аппарате колеса гидротурбины. В качестве электропроводного материала он использовал листы константана, в которых вырезались исследуемые решетки профилей направляющих аппаратов гидротурбин. Листы зажимались в медных шинах, к которым подводился электрический ток (постоянный). Широкое применение метод ЭГДА получил для решения задач обтекания турбинных и компрессорных решеток. На установке ЭГДА может быть непосредственно исследовано обтекания тел поступательно-циркуляционным потоком. Для решения практически важных задач необходимо уметь определять значение скоростей и давлений не только в контуре профиля, но и в любой точке исследуемой области поступательно-циркуляционного потока. Аналитическое решение такой задачи для одиночного профилятребует чрезвычайно сложных и громоздких вычислений. Для решетки профилей аналитическое решение подобной задачи неизвестно. Поэтому можно воспользоваться методом ЭГДА. Этим методом решались задачи обтекания тел плоским потоком сжимаемого газа с дозвуковой скоростью (используется электролитическая ванна с переменной глубиной электролита), нелинейные задачи газодинамики, обтекания крылового профиля, движения трехмерных потоков несжимаемой
жидкости в проточной части турбомашин. Широкое применение нашел метод электрогидродинамической аналогии в вихревых полях (ВЭГА).

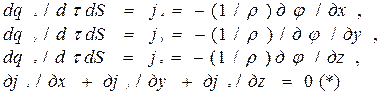Для установления аналогов рассмотрим уравнения движения электрических зарядов в проводниках:

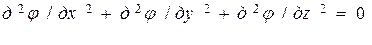Подставив первые три уравнения в уравнение (*), получим:

В уравнениях j – плотность электрического тока, φ – электрический потенциал, ρ – удельное сопротивление проводника. Первые три уравнения представляют собой математическую запись закона Ома, уравнение, помеченное (*) – запись закона сохранения заряда.

Для потенциального течения несжимаемой жидкости:

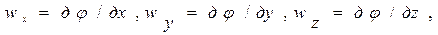
Уравнение неразрывности для несжимаемой жидкости имеет вид

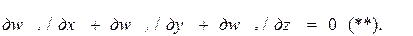
Подставив первые три уравнения в уравнение (**), получим

,

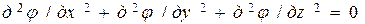где φ(x,y,z,τ) – потенциал скоростей.

Потенциал скоростей аналогичен электрическому потенциалу, удельная плотность электрического тока - скорости. Если область течения электрического тока подобна области течения жидкости, а граничные условия аналогичны, то интегралы уравнений Лапласа для этих функций будут отличаться лишь произвольными постоянными. Эквипотенциальные поверхности в электрическом поле тождественны эквипотенциальным поверхностям в потоке жидкости. Силовые линии электрического поля тождественны линиям тока в потоке жидкости.

Это трехмерный случай. В двумерном случае, при геометрическом подобии областей, когда граничные условия для электрического потенциала тождественны граничным условиям для потенциала скоростей, эквипотенциальные линии в электрическом поле тождественны эквипотенциальным линиям в потоке жидкости, силовые линии электрического поля тождественны линиям тока в жидкости.

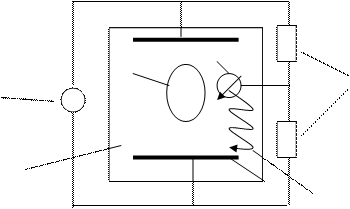
Установка ЭГДА состоит из двух основных частей: моделии электрической схемы. Модельпредставляет собой область движения электрического тока, предназначенную воспроизводить исследуемую область движения жидкости. Для ее создания используют различные электропроводные материалы в сочетании с диэлектриками, образующими границы области. Электрическая схема ЭГДА состоит из питательной и измерительной цепей и контрольно-измерительных приборов. Все существующие установки ЭГДА работают по принципу мостовой или компенсационной схемы (или комбинированной).

1 7

2 =

4 5

1-модель из диэлектрика, 2 - источник постоянного или переменного тока; 3 – водный раствор соли, 4 – шина; 5 – щуп, 6- резисторы, 7 – гальванометр

Рисунок 2.1 - Установка ЭГДА

Для идеальной жидкости функция тока удовлетворяет уравнению Лапласа. Гармонически сопряженная с ней функция – потенциал скоростей потока. Линии равных потенциалов и равных функций тока ортогональны. Распределение температуры в двумерном поле также подчиняется уравнению Лапласа, т.е. линии теплового потока и температурного потенциала аналогичны линиям тока и потенциалу скоростей идеального потока жидкости (гидротепловая аналогия).

Электротепловая аналогия заключается в том, что перенос тепла аналогичен переносу электрических зарядов (электропроводность аналогична теплопроводности).

Поток электрического заряда (сила тока):

I=Δq/Δτ = Δφ γ S/Δl= Δφ/R_Э

Тепловой поток:

q_Т=ΔQ/Δτ = ΔТ λ S/Δl= ΔТ/R_Т

Таким образом, тепловое сопротивление аналогично электрическому.

λ

γ

Т₁ R_T= Δl/λS φ₁ φ₂

Δl

Т₂

R_Э= Δl/γS

Δl

Рисунок 2.2 - Одномерная модель стационарной теплопроводности через однослойную стенку и ее электрический аналог

λ1

Т₁

λ2

λ3

γ1

γ3

γ2

φ₁ φ₂ φ₃ φ₄

Т₂ Δl₁ Δl₂ Δl₃

Т₃ R_Э1 R_Э2 R_Э3

Т₄

Δl₁ Δl₂ Δl₃

R_T1 R_T2 R_T3

Рисунок 2.3 - Одномерная модель стационарной теплопроводности через многослойную стенку и ее электрический аналог (последовательное соединение слоев)

При последовательном соединении слоев по аналогии с теорией электричества

q_т=ΔT₁₄/(Rт₁+ Rт₂+ Rт₃).

Электротепловую аналогию можно использовать и для решения более сложных задач. Например, если теплопроводность протекает в материалах, расположенных параллельно.

γ1

λ1

Т₁ R_Э1

R_T1

γ2

λ2

φ₁ φ₂

R_T2

Т₂ R_Э2

Рисунок 2.4 - Одномерная модель стационарной теплопроводности через многослойную стенку и ее электрический аналог (параллельное соединение слоев)

При этом по аналогии с теорией электричества

q_т=ΔT₁₂/(1/Rт₁+ 1/Rт₂).

К достоинству метода можно отнести: простоту электрической схемы, простоту измерения напряжения, большую точность результатов.

При разработке электрических моделей, имитирующих процессы теплопроводности, применяются два способа. В первом электрическая модель повторяет геометрию оригинальной тепловой системы и изготавливается из материала с непрерывной проводимостью. Такие модели – с непрерывными параметрами процесса. Во втором – тепловые системы заменяются электрическими цепями. Модели при этом будут с сосредоточенными параметрами процесса.

Метод исследования, основанный на идее физической аналогии, является наиболее сильным средством обобщенного анализа. Из курса физики вам известно, что существует тройная аналогия в явлениях переноса. Аналогия объединяет в единое целое разнородные явления, воспринимаемые как теплообмен, массообмен и гидродинамическое сопротивление. Аналогия является следствием единого молекулярного физического механизма процессов.

Уравнение Фурье (теплопроводность)

q = - λgrad T,

уравнение Фика (диффузия)

j = - D grad с,

уравнение Ньютона (вязкость)

σ = - η grad u.

Большинство промышленных технических объектов являются сложными системами. Характерные признаки сложной системы: невозможность рассмотрения отдельно каждого ее элемента (без установления связей с другими элементами и внешней средой); неопределенность в большом числе состояний системы; неопределенность достоверности информации; разнообразие вариантов достижения конечной цели функционирования системы; адаптивность (приспособляемость системы к возмущающим факторам воздействия среды).

Характерные особенности сложных систем вызывают необходимость использования в ходе создания их моделей методологии системного подхода.

Система -совокупность элементов, находящихся в отношениях и связях друг с другом, которая образует определенную целостность, единство.

Системные принципы:

- целостности (принципиальная не сводимость свойств системы к сумме свойств составляющих ее элементов и не выводимость из последних свойств целого);

- структурности (возможность описания системы через установление ее структуры, т.е. сети связей и отношений системы; обусловленность поведения системы не столько поведением ее отдельных элементов, сколько свойствами ее структуры);

- взаимозависимости системы и среды (система формирует и проявляет свои свойства в процессе взаимодействия со средой, являясь при этом активным, ведущим компонентом взаимодействия);

- иерархичности (каждый компонент системы в свою очередь может рассматриваться как система, а используемая в данном случае система представляет один из компонентов более широкой системы);

- множественности описания каждой системы.

Важной особенностью систем является передача в них информации и наличие процессов управления.

Системы бывают: замкнутые, открытые, статичные, динамичные, детерминированныеивероятностные.

Математическое описание модели в общем случае можно представить так

Y(τ)= F(X(τ), V(τ), S(τ), τ),

где F – закон функционирования системы;

X(τ) - входные параметры;

V(τ) - воздействия внешней среды;

S(τ) - собственные параметры системы;

Y(τ) - выходные параметры;

τ - время.

Параметры X,V,S часто называют экзогенными (независимыми), а Y - эндогенными (зависимыми).

Существует определенная последовательность реализации моделирования, показанная на схеме рис.2.5.

Основным количественным критерием адекватности модели является степень соответствия вычислительного эксперимента данным экспериментальных работ. При отсутствии последних или для предварительного анализа критерием можно считать непротиворечивость полученных результатов принятым при моделировании гипотезам и допущениям, а так же здравому смыслу.

Любая созданная модель должна удовлетворять ряду требований:

- адекватность ее объекту;

- доступность, простота и понятность для пользователя;

- универсальность (ее модули должны легко адаптироваться к другим модулям;

- точность (высокое совпадение результатов вычислительного эксперимента и параметров реального объекта);

- устойчивость и достоверность функционирования в широком диапазоне изменения рабочих параметров;

- открытость и модульность, способность к развитию без существенного изменения базового варианта;

- экономичность, реализуемая с помощью сравнительно простых алгоритмов и программ, не требующих больших ресурсов ВТ.

Многие из перечисленных требований противоречат друг другу, что требует от разработчиков добиться их оптимального сочетания в зависимости от поставленной цели моделирования.

Рисунок 2.5 – Схема последовательности реализации моделирования

Использование системного подхода в некоторой степени ускоряет процесс моделирования, поскольку предлагает разработчику методологию моделирования. Конкретизация этапов моделирования позволяет систематизировать виды его обеспечения: математическое, программное, информационное и техническое.

Можно предложить ряд средств ускорения моделирования в области этих видов обеспечения.

При решении задач моделирования сложных систем приходится периодически использовать разнообразную информацию, для тепловых процессов необходимы три группы данных: об индивидуальных свойствах газообразных и конденсированных веществ; о свойствах газообразных, жидких и твердых топлив; о химических реакциях и механизме их протекания. Выполнение требования адекватности математической модели невозможно без соблюдения требования максимальной достоверности этой информации. Для ее хранения используются банки данных (БнД). Преимущество использования БнД для информационного обеспечения при моделировании заключается в том, что с помощью системы управления базой данных (СУБД) программы прикладной области получают необходимую информацию из базы данных. Это позволяет представлять данные независимо от структуры прикладных программ в наиболее удобной логической форме и соответственно обеспечивает независимость прикладных программ от данных.

Принципиально новые возможности появляются при использовании в математическом моделировании и вычислительном эксперименте инструментальных систем (ИС). ИС принято называть программную систему, средства которой могут быть использованы для создания и развития пакетов прикладных программ (ППП) и прикладных программных комплексов (ППК) и для накопления базы знаний (БЗ), т.е. формализованной совокупности сведений о некоторой предметной области, содержащей данные о свойствах объектов, закономерностях процессов и явлений и правила использования этих знаний для принятия решения.

Оперативность моделирования обеспечивается следующими качествами ИС: возможностью оперирования языковыми конструкциями конкретной предметной области; автоматическим синтезом программ; возможностью оперативного рассмотрения различных вариантов математических моделей и их модификаций; организацией « дружественного интерфейса», состоящего в интерактивном диалоговом взаимодействии пользователя и системы с выполнением требований простоты и удобства общения для пользователя. Степень целесообразности использования ИС для решения задач математического моделирования зависит от их структуры, оценки уровня сложности модели, требований к ней, квалификации пользователя моделью.

Литература: [5],[13-18].

Лекция 3