Функции для проведения регрессии.

• Функции для линейной регрессии.
• Функция для линейной регрессии общего вида.
• Функции для одномерной и многомерной полиномиальной регрессии.
• Функция для нелинейной регрессии общего вида..

Функции для линейной регрессии.

Другой широко распространенной задачей обработки данных является представление их совокупности некоторой функцией у(х). Задача регрессии заключается в получении параметров этой функции такими, чтобы функция приближала облако исходных точек (заданных векторамиVX и VY) с наименьшей среднеквадратичной погрешностью.

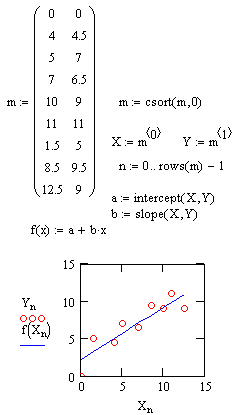Чаще всего используется линейная регрессия, при которой функция у(х) имеет вид у(х) = а + b*х и описывает отрезок прямой. К линейной регрессии можно свести многие виды нелинейной регрессии при двупараметрических зависимостях у(х). Для проведения линейной регрессии в систему встроен ряд приведенных ниже функций: corr(VX, VY) — возвращает скаляр — коэффициент корреляции Пирсона; intercrpt(VX, VY) — возвращает значение параметра а (смещение линии регрессии по вертикали); slope(VX, VY) — возвращает значение параметра b (наклона линии регрессии).

Функция для линейной регрессии общего вида.

В MathCAD реализована возможность выполнения линейной регрессии общего вида. При ней заданная совокупность точек приближается функцией вида:

F(x, K1, К2,..., Kn)=K1*F1(x)+K2*F2(x)+…+Kn*Fn(x).

Таким образом, функция регрессии является линейной комбинацией функций F1(x), F2(x),..., Fn(x), причем сами эти функции могут быть нелинейными, что резко расширяет возможности такой аппроксимации и распространяет ее на нелинейные функции.

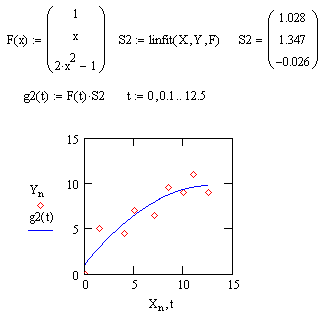Для реализации линейной регрессии общего вида используется функция linfit(VX,VY,F). Эта функция возвращает вектор коэффициентов линейной регрессии общего видаК, при котором среднеквадратичная погрешность приближения облака исходных точек, если их координаты хранятся в векторах VX и VY, оказывается минимальной. Вектор F должен содержать функции F1(x), F2(x),..., Fn(x), записанные в символьном виде.

Расположение координат точек исходного массива может быть любым, но векторVX должен содержать координаты, упорядоченные в порядке их возрастания, а векторVY — ординаты, соответствующие абсциссам в вектореVX.

Функции для одномерной и многомерной полиномиальной регрессии.

Введена в новую версию MathCAD и функция для обеспечения полиномиальной регрессии при произвольной степени полинома регрессии:

regress(VX,VY, n)

Она возвращает векторVS, запрашиваемый функцией interp(VS,VX,VY,x), содержащий коэффициенты многочлена n-й степени, который наилучшим образом приближает “облако” точек с координатами, хранящимися в векторахVX и VY.

Для вычисления коэффициентов полинома регрессии используется функция submatrix.

На практике не рекомендуется делать степень аппроксимирующего полинома выше четвертой — шестой, поскольку погрешности реализации регрессии сильно возрастают.

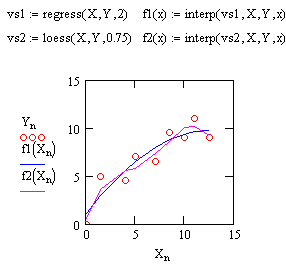Функция regress создает единственный приближающий полином, коэффициенты которого вычисляются по всей совокупности заданных точек, т. е. глобально. Иногда полезна другая функция полиномиальной регрессии, дающая локальные приближения отрезками полиномов второй степени,— loess(VX, VY, span). Эта функция возвращает используемый функцией interp(VS,VX,VY,,r) вектор VS, дающий наилучшее приближение данных (с координатами точек в векторахVX и VY) отрезками полиномов второй степени. Аргумент span>0 указывает размер локальной области приближаемых данных (рекомендуемое начальное значение — 0,75).

Чем больше span, тем сильнее сказывается сглаживание данных. При больших span< эта функция приближается к regress(VX,VY,2).

MathCAD позволяет выполнять также МНОГОМЕРНУЮ регрессию, самый типичный случай которой — приближение трехмерных поверхностей. Их можно характеризовать массивом значений высот z, соответствующих двумерному массивуМху координат точек (х, у) на горизонтальной плоскости.

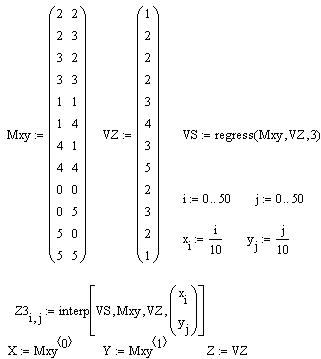Новых функций для этого не задано. Используются уже описанные функции в несколько иной форме: Regress (Mxy, Vz, n) — возвращает вектор, запрашиваемый функцией interp (VS,Mxy,Vz,V) для вычисления многочлена п-й степени, который наилучшим образом приближает точки множестваМху и Vz. Мху — матрица mx2, содержащая координаты x и y. Vz — m-мерный вектор, содержащий z-координат, соответствующих m точкам, указанным в Mxy;

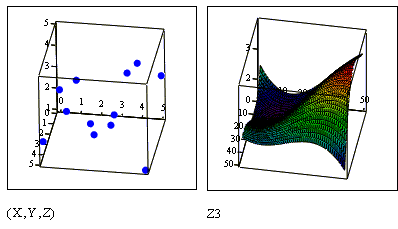
loes(Mxy,Vz,span) — аналогичнаloes(VX,VY, span), но в многомерном случае; interp (VS,Mxy,Vz,V) — возвращает значение z по заданным векторамVS(создается функциямиregress или loess) и Мху, Vz и V (вектор координат х и узаданной точки, для которой находится z).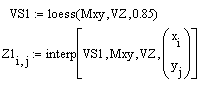

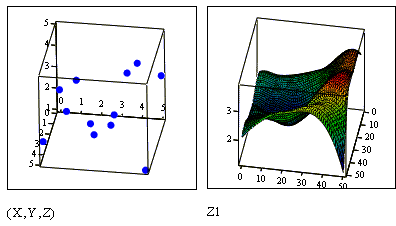
Функция для нелинейной регрессии общего вида.

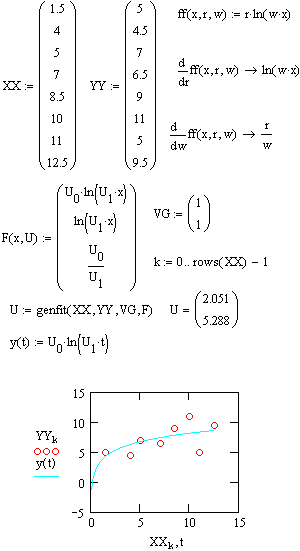Под нелинейной регрессией общего вида подразумевается нахождение вектора К параметров произвольной функции F(x,K1,K2,...,Kn), при котором обеспечивается минимальная среднеквадратичная погрешность приближения облака исходных точек. Для проведения нелинейной регрессии общего вида используется функцияgenfit(VX, VY, VS,F). Эта функция возвращает вектор К параметров функции F, дающий минимальную среднеквадратичную погрешность приближения функциейF(x,Kl,K2,...,Kn) исходных данных. F должен быть вектором с символьными элементами, содержащими уравнение исходной функции и ее производных по всем параметрам. ВекторVS должен содержать начальные значения элементов вектораК, необходимые для решения системы нелинейных уравнений регрессии итерационным методом.

Функции сглаживания данных.

Данные большинства экспериментов имеют случайные составляющие погрешности. Поэтому часто возникает необходимость статистического сглаживания данных. Ряд функций MathCAD предназначен для выполнения операций сглаживания данных различными методами. Вот перечень этих функций:

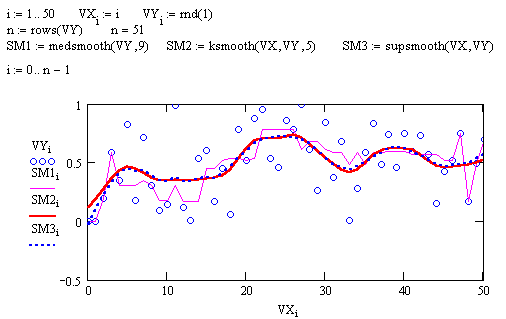
medsmooth(VY,n)— для вектора с m действительными числами возвращает m-мерный вектор сглаженных данных по методу скользящей медианы, параметр n задает ширину окна сглаживания (n должно быть нечетным числом, меньшим m);

ksmooth(VX,VY, b) — возвращает n-мерный вектор сглаженныхVY, вычисленных на основе распределения Гаусса.VX и VY — n-мерные векторы действительных чисел. Параметр b(полоса пропускания) задает ширину окна сглаживания ( b должно в несколько раз превышать интервал между точками по оси х );

supsmooth(VX, VY) — возвращает n-мерный вектор сглаженныхVY, вычисленных на основе использования процедуры линейного сглаживания методом наименьших квадратов по правилу k-ближайших соседей с адаптивным выбором k.VX и VY — n-мерные векторы действительных чисел. Элементы вектора VX должны идти в порядке возрастания.

Функция предсказания.

Весьма интересной является функция предсказания predikt(data,k,N), где data — вектор данных,

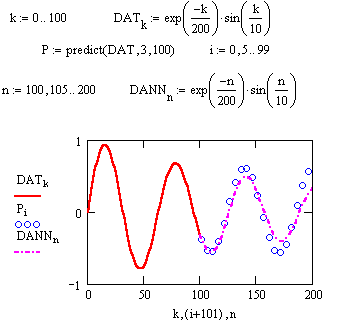где data — вектор данных, k — число последних точек существующих данных, на основе которых происходит расчет предсказываемых точек; и N — число точек, в которых необходимо предсказать данные. Она по ряду заданных равномерно расположенных точек позволяет рассчитать некоторое число N последующих точек, т. е. по существу выполняет экстраполяцию произвольной (но достаточно гладкой и предсказуемой) зависимости.

Функция предсказания обеспечивает высокую точность при монотонных исходных функциях или функциях, представляемых полиномом невысокой степени.