Степенная функция с рациональным (дробным) показателем

Степенная функция с рациональным (дробным) показателем

Рассмотрим степенную функцию y = x ^p с рациональным (дробным) показателем степени , где n – целое, m > 1 – натуральное. Причем, n, m не имеют общих делителей.

Знаменатель дробного показателя - четный

Пусть знаменатель дробного показателя степени четный: m = 2, 4, 6, ... . В этом случае, степенная функция x ^p не определена для отрицательных значений аргумента. Ее свойства совпадают со свойствами степенной функции с иррациональным показателем (см. следующий раздел).

Арксинус, arcsin

Арксинус ( y = arcsin x ) – это функция, обратная к синусу ( x = sin y ). Он имеет область определения и множество значений .
sin(arcsin x) = x
arcsin(sin x) = x

Арксинус иногда обозначают так:
.

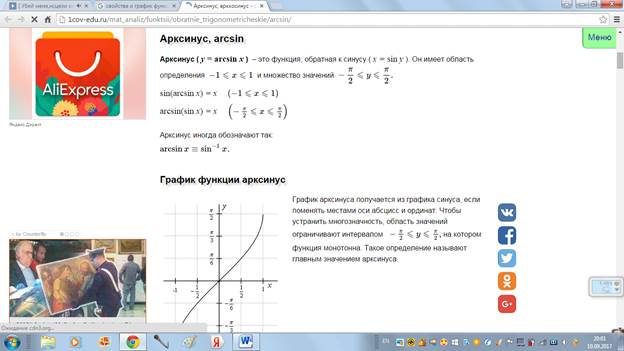
График функции арксинус

График функции y = arcsin x

График арксинуса получается из графика синуса, если поменять местами оси абсцисс и ординат. Чтобы устранить многозначность, область значений ограничивают интервалом , на котором функция монотонна. Такое определение называют главным значением арксинуса.

Арккосинус, arccos

Арккосинус ( y = arccos x ) – это функция, обратная к косинусу ( x = cos y ). Он имеет область определения и множество значений .
cos(arccos x) = x
arccos(cos x) = x

Арккосинус иногда обозначают так:
.

График функции арккосинус

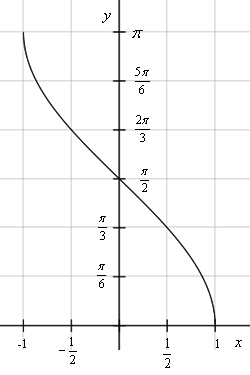
График функции y = arccos x

График арккосинуса получается из графика косинуса, если поменять местами оси абсцисс и ординат. Чтобы устранить многозначность, область значений ограничивают интервалом , на котором функция монотонна. Такое определение называют главным значением арккосинуса.

Четность

Функция арксинус является нечетной:
arcsin(–x) = arcsin(–sin arcsin x) = arcsin(sin(–arcsin x)) = – arcsin x

Функция арккосинус не является четной или нечетной:
arccos(–x) = arccos(–cos arccos x) = arccos(cos(π–arccos x)) = π – arccos x ≠ ± arccos x

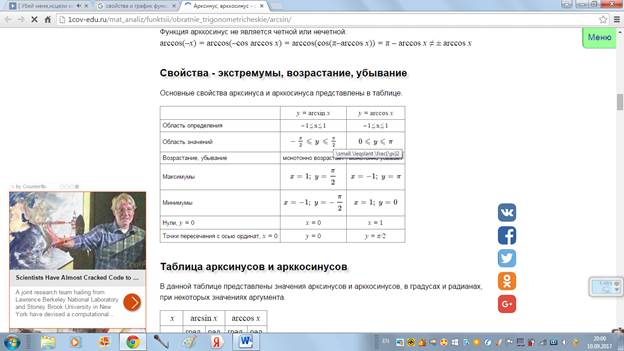
Свойства - экстремумы, возрастание, убывание

Основные свойства арксинуса и арккосинуса представлены в таблице.

	y = arcsin x	y = arccos x
Область определения	– 1 ≤ x ≤ 1	– 1 ≤ x ≤ 1
Область значений
Возрастание, убывание	монотонно возрастает	монотонно убывает
Максимумы
Минимумы
Нули, y = 0	x = 0	x = 1
Точки пересечения с осью ординат, x = 0	y = 0	y = π/2

10) Arctg x

Арктангенс, arctg

Арктангенс ( y = arctg x ) – это функция, обратная к тангенсу ( x = tg y ). Он имеет область определения и множество значений .
tg(arctg x) = x
arctg(tg x) = x

Арктангенс обозначается так:
.

График функции арктангенс

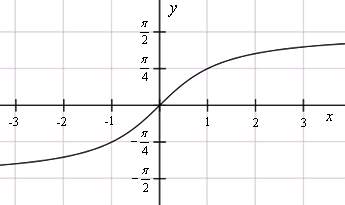
График функции y = arctg x

График арктангенса получается из графика тангенса, если поменять местами оси абсцисс и ординат. Чтобы устранить многозначность, множество значений ограничивают интервалом , на котором функция монотонна. Такое определение называют главным значением арктангенса.

Арккотангенс, arcctg

Арккотангенс ( y = arcctg x ) – это функция, обратная к котангенсу ( x = ctg y ). Он имеет область определения и множество значений .
ctg(arcctg x) = x
arcctg(ctg x) = x

Арккотангенс обозначается так:
.

График функции арккотангенс

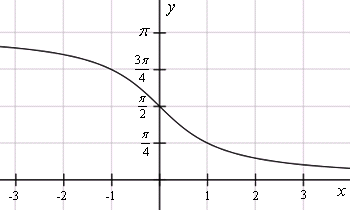
График функции y = arcctg x

График арккотангенса получается из графика котангенса, если поменять местами оси абсцисс и ординат. Чтобы устранить многозначность, область значений ограничивают интервалом , на котором функция монотонна. Такое определение называют главным значением арккотангенса.

Четность

Функция арктангенс является нечетной:
arctg(–x) = arctg(–tg arctg x) = arctg(tg(–arctg x)) = – arctg x

Функция арккотангенс не является четной или нечетной:
arcctg(–x) = arcctg(–ctg arcctg x) = arcctg(ctg(π–arcctg x)) = π – arcctg x ≠ ± arcctg x.

Степенная функция с рациональным (дробным) показателем

Рассмотрим степенную функцию y = x ^p с рациональным (дробным) показателем степени , где n – целое, m > 1 – натуральное. Причем, n, m не имеют общих делителей.