Определение случайной величины

СЛУЧАЙНЫЕ ВЕЛИЧИНЫ

На начальных стадиях развития теории вероятностей появилась необходимость связывать различные случайные события с действительными числами и вести расчеты последних. Так, уже задача проведения испытаний, рассмотренная Я. Бернулли, требовала введения в рассмотрение числа появлений изучаемого события А при заданном числе испытаний. В результате возникло новое понятие – случайная величина (случайная переменная). Поэтому основное направление дальнейших исследований в теории вероятностей сместилось в сторону изучения и развития понятия случайной величины, ее функции распределения и связанных со случайной величиной закономерностей.

Вопросы для самопроверки

1.С какой целью вводится случайная величина?

2. Сформулируйте определение случайной величины.

3. Что является множеством значений случайной величины?

4.Какие множества образут алгебру ?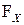

5.Как задается распределение вероятностей случайной величины?

Вопросы для самопроверки

1.Какую вероятность определяет функция распределения?

2.В каких пределах изменяется значение функции распределения?

3.Перечислите свойства функции распределения.

4.По какой формулевычислется вероятность того, что значения случайной величины принадлежат некоторому промежутку?

5.Как вычислить вероятность отдельного значения случайной величины ?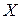

6.При каких значениях 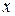функция распределения равна нулю и единице?

7.Как вычислить вероятность того, что значения случайной величины 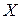больше некоторого числа ?

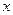Вопросы для самопроверки

1.Сформулируйте определение дискретной случайной величины .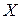

2.Как определяется вероятность события ?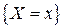

3.Сформулируйте определение закона распределения дискретной случайной величины .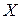

4.В какой форме задается закон распределения дискретной случайной величины ?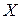

5.Что является графиком ряда распределения?

6.Как вычислить вероятность события ?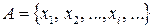

7.Как вычислить функцию распределения 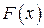дискретной случайной величины 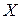и построить ее график?

8.Чему равна вероятность того, что значения дискретной случайной величины 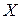принадлежат промежутку ?

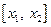Вопросы для самопроверки

1.Чем отличаются дискретные случайные величины от непрерывных случайных величин?

2.Почему для непрерывных случайных величин невозможно построить ряд распределения?

3.Что характеризует элемент вероятности ?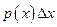

4.Как вычислить вероятность попадания непрерывной случайной величины на промежуток?

5.Как вычислить функцию распределения 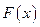непрерывной случайной величины ?

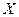6.Почему плотность распределения 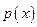непрерывной случайной величины 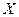является неотрицательной функцией?

7.Чему равна вероятность отдельного значения 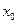непрерывной случайной величины ?

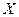Тогда

Предположим далее, что это свойство выполняется для произведения случайной величины, т.е.

идокажем, что оно выполняется для произведения п случайных величин. Дпя этого введем обозначение .

Тогда по доказанному, а по предположению. Следовательно, , что и требовалось доказать.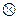

4^о. Математическое ожидание суммы нескольких случайных величин равно сумме математических ожиданий слагаемых:

Доказательство. Пусть заданы две случайные величины Х₁ и Х₂ рядами распределения (см. табл. 2.1 и 2.2).

В силу вышесказанного возможные значения случайной величины Х₁ + Х₂ будут . Их вероятности равны , так как они определяются по теореме умноже-ния вероятностей. Действительно, вероятность Р(х_i+х_j) обозначает вероятность того, что события и наступают совместно (одновременно),т.е.

Переходя к математическому ожиданию рассматриваемой суммы,имеем

Предположим далее, что свойство 4° справедливо для п–1 случайной величины:

Тогда, введя обозначение , получим, что

по доказанному, а по предположению. Следовательно,

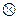
Дисперсия случайной величины. На практике часто требуется оценить рассеивание возможных значений случайной величины вокруг ее среднего значения. На первый взгляд может показаться, что проще всего вычислить все возможные значения отклонения (разность между значением случайной величины и ее математическим ожиданием называется отклонением и обозначается Х–М(Х)) Х – М(Х) случайной величины и затем найти их среднее значение. Однако среднее арифметическое отклонений может быть равно нулю, хотя сами отклонения будут большими по модулю. Это объясняется тем, что значения могут иметь противоположные знаки и взаимно погашаться при нахождении среднего арифметического. Поэтому для характеристики рассеивания вычисляют дисперсию и среднее квадратическое отклонение.

Определение 2.11. Дисперсией случайной величины называется математическое ожидание квадрата ее отклонения:

D(Х) = М(Х- М(Х))².

Применив определение математического ожидания, получим формулы для вычисления дисперсии случайной величины Х:

(2.10)

Дисперсию случайной величины можно вычислять, применяя следующую теорему.

Теорема 2.5. Дисперсия случайной величины равна математическому ожиданию ее квадрата минус квадрат математического ожидания:

D(Х) = М(Х²) — (М(Х))² .

Доказательство. Действительно, из определения 2.11 с помощью тождественных преобразований, учитывая, что М(Х), –2М(Х), М²(Х) – постоянные величины, получим утверждение теоремы:

D(Х) = М(Х – М(Х))² =М(Х² - 2ХМ(Х) + (М(Х))²) =

= М(Х²) - 2(М(Х))² + (М(X)²) = М(Х²) - (М(X))² .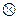

Тогда формулы (2.10) примут следующий вид:

(2.11)

Свойства дисперсии.Дисперсия спучайной величины удовлетворяет следующим свойствам.

1^о. Дисперсия постоянной величины С равна нулю: D(С)=0. Действительно, D(С) =М(С–М(С))² =М(С–С) = 0.

2^о. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат: D(СХ) =С²D(Х).

Доказательство. По определению 2.11 и в силу свойств математического ожидання, получим:

D(CХ) =М(СХ–М(СХ))²=М(СХ–СМ(Х))²=М(С(Х–М(Х)))²=

=M(C²(Х–М(Х))²)=С²M(Х–M(X))²=C²D(X).

3^о. Дисперсия суммы нескольких независимых случайных величин равна сумме дисперсий этих величин:

Доказательство. Докажем вначале, что

По теореме 2.5 дисперсию суммы можно вычислить по формуле:

Предположим далее, что дисперсия суммы случайной величины равно сумме дисперсий

и докажем свойство 3^о для п случайных величин. Обозначим , тогда по доказанному, а по предположению. Следовательно,

Следствие 1. Дисперсия суммы постоянной величины С и случайной величины равна дисперсии случайной величины Х: D(С+Х) = D(Х). Действительно, D(С+X) =D(С)+D(X) =0+D(X) =D(X).

Следствие 2. Дисперсия разности двух независимых случайных величин Х и Y равна сумме их дисперсий: D(Х – Y) = D(Х) + D(Y) .

Доказательство. Используя свойства 2° и 3° , получаем

D(X – Y) = D(X)+D(–Y) = D(X) + (–1)² D(Y) = D(X) +D(Y) .

Дисперсия случайной величины как характеристика рассеивания имеет одну неприятную особенность: ее размерность, как видно из определения дисперсии, равна квадрату размерности случайной величины Х. Поэтому для характеристики отклонений случайной величины Х, имеющих размерность, одинаковую с размерностью случайной величины, вводится приведенное ниже определение.

Определение 2.12. Средним квадратическим отклонением (стандартом) случайной величины Х называется арифметический корень из дисперсии, т.е. .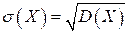

Таким образом, зная введенные две числовые характеристики – математическое ожидание М(Х) и среднее квадратическое отклонение , –получаем ориентировочное представление о пределах возможных значений случайной величины.

Моменты распределения случайных величин. Обобщением основных числовых характеристик случайных величин, описывающих центр распределения (математического ожидания, моды, медианы) и рассеивание (дисперсии и среднего квадратического отклонения), является понятие моментов случайных величин.

Определение 2.13. Начальным моментом k-го порядка случайной величины Х называется математическое ожидание k-й степени этой случайной величины, т.е., .

Из определения математического ожидания для дискретных и непрерывных случайных величин, получаем формулы для вычисления начальных моментов:

Определение 2.14. Центральным моментом порядка k случайной величины Х называется математическое ожидание k-й степени отклонения Х–М(Х), т.е.

Согласно определению математического ожидания случайной величины Х, получим следующие формулы для вычисления центральных моментов k-го порядка:

Следует отметить, что начальный момент первого порядка – это математическое ожидание, а центральный момент второго порядка – это дисперсия. Третий центральный момент служит характеристикой асимметрии ("скошенности") распределения. Для получения безразмерной характеристики делят на . Отношение называется коэффициентом асимметрии и обозначается . Если распределение симметрично относительно математического ожидания, то все моменты нечетного порядка равны нулю.

Если кривая плотности распределения непрерывной случайной величины такова, что справа от моды расположена ее "длинная часть", а слева – "короткая часть", то коэффициент S_k асимметрии положителен. Коэффициент асимметрии S_k отрицателен, когда "длинная часть" кривой плотности распределения расположена слева от моды. На рис. 2.13 показаны кривые плотности распределения с положительной и отрицательной асимметриями.

Рис. 2.13

Четвертый центральный момент является характеристикой "крутости", т.е. островершинности или плосковершинности распределения. Эти свойства описываются с помощью эксцесса, т. е. величины .

Число 3 вычитается из отношения , так как все распределения сравниваются с нормальным распределением, с которым мы познакомимся позже, для которого .

Кривые, более островершинные по сравнению с кривой закона нормального распределения, обладают положительным эксцессом. Кривые более плосковершинные – отрицательным эксцессом.

Пример 2.6. Продавец мороженого в солнечный день может, продать мороженого на 60 ден. ед. а в дождливый — на 20 ден. ед. Какова ожидаемая дневная выручка, если вероятность того, что день окажется дождливым, равна 0,35?

Решение. Ряд распределения случайной величины Х – возможная выручка в дождливый и солнечный дни имеет вид:

xi
pi	0,35	0,65

Так как Х - дискретная случайная величина и ожидаемая выручка – это математическое ожидание М(Х) = 20∙0,35+160∙0,65 = 7 +104 = 111, то продавец может продать мороженого на 111 ден. ед.

Среднее квадратическое отклонение ожидаемой выручки вычислим по формуле

Ответ:ожидаемая дневная выручка, равна 111 ден.ед.

Пример 2.7. Случайная величина задана плотностью распределения вероятностей:

Определить математическое ожидание и дисперсию этой случайной величины.

Решение. Используя формулу (2.9), вычисляем математическое ожидание:

(Для вычисления интеграла мы применили формулу интегрирования по частям).

По формуле (2.11) дисперсия

(Интеграл вычисляем дважды, применяя формулу интегрирования по частям).

Ответ:математическое ожидание равно 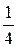, а дисперсия – 0,47.

Пример 2.8. Пусть случайная величина Z имеет вид . Найти математическое ожидание и дисперсию случайной величины Z.

Решение. Таккак случайная величии Х и число М(Х) независимы, то, воспользовавшись свойствами математического ожидания и дисперсии, можно записать:

так как , поскольку постоянная величина.

Ответ:математическое ожидание и дисперсия случайной величины Z, соответственно равны 0 и 1.

Случайные величины, для которых математическое ожидание равно нулю, а дисперсия равна единице, называются центрированными.

Вопросы для самопроверки

1.Что характеризует математическое ожидание случайной величины ?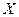

2.По каким формулам вычисляютсяматематические ожидания дискретной и непрерывной случайной величины ?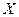

3.Перечислите другие числовые характеристики положения значений случайной величины .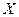

4.Докажите свойства математического ожидания случайной величины .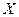

5.Укажите характеристики рассеяния значений случайной величины 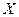и формулы для их вычисления.

6.Докажите свойства дисперсии случайной величины.

7.Сформулируйте определения начальных и центральных моментов и выпишите формулы для их вычисления.

8.Какие показатели характеризуют асимметрию и островершинность кривых распределений?

Дискретные распределения

Биномиальное распределение. Проведение эксперимента, в результате которого может произойти некоторое элементарное событие , , назовем испытанием. Причем подразумевается, что эксперимент может быть повторен при неизменных условиях 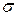сколь угодно большое число раз. Два испытания будем называть независимыми, если вероятности произведения элементарных событий этих испытаний определяются по формуле , где – элементарное событие первого испытания; – элементарное событие второго испытания. Аналогично определяется независимость п испытаний, т.е. если для любого возможного результата п испытаний , где – результат первого испытания, – результат второго испытания, …, – результат п-го испытания, вероятность вычисляется по формуле

,

то испытания назовем независимыми.

Остановимся на простейшем случае повторения одного и тогоже испытания при неизменных условиях, причем каждое испытание имеет два возможных исхода (два возможных элементарных события и . Вероятность появления элементарного события для каждого испытания постоянна и равна р, где 0 < р < 1. Такие испытания получили название схемы Бернулли.

Биномиальное распределение является вероятностным законом последовательности независимых испытаний Бернулли.

Простейшей задачей, относящейся к испытаниям Бернулли, является отыскание вероятности Р_п(т) того, что некоторое событие А наступит т раз при п испытаниях, а остальные п–т раз наступит противоположное событие .

Для решения этой задачи введем случайную величину Х – число появлений события А в п независимых испытаниях. Эту случайную величину можно представить в виде суммы случайных величин X_i, где X_i – число появления события А в i-м испытании, т.е. , причем множество значений каждой случайной величины имеет вид: – событие А наступило в i-м испытании; – событие А не наступило в i-м испытании. Предположим, что вероятность того, что событие А наступило в i-том испытании, , а вероятность того, что событие А не наступило в i-том испытании, .

Пусть произведено п независимых испытаний. Результат каждого испытания будем отмечать буквой А, если событие А наступило, и буквой , если событие А не наступило. Предположим вначале, что событие А наступило в т первых испытаниях, а в остальных п–т испытаниях наступило событие . Тогда по теореме умножения независимых событий вероятность этого результата п независимых испытаний равна .

Но событие А может произойти в любых т испытаниях и число таких способов наступления события А т раз в п испытаниях будет равно числу сочетаний из п элементов по т, т. е. , и все результаты несовместны. Тогда, по теореме сложения вероятностей для несовместных событий, вероятность наступления события А т раз в п испытаниях равна , т.е.

(2.11)

Формула (2.11) называется формулой Бернулли. Число сочетаний из элементов по можно вычислить по формулам: или .

Появление события А т раз в п испытаниях, равносильно тому, что случайная величина Х приняла значение, равное т. Следовательно, случайная величина , являясь дискретной случайной величиной, принимает целочисленные значения от 0 до п и ее множество значений определяется множеством: . Ряд распределения случайной величины Х имеет следующий вид:

хi				…	n
pi				…

и называется биномиальным распределением, потому что вероятности можно рассматривать как члены бинома (q+р)^п.

Функция F(х) дискретной случайной величины Х, распределенной по биномиальному закону, определяется формулой

.

Числовые характеристики случайной величины Х – числа появлений события А в п независимых испытаниях — определяются достаточно просто. Покажем это.

Математическое ожидание числа появлений события А в п независимых испытаниях, т. е. случайной величины X, распределенной по биномиальному закону, равно произведению числа испытаний и вероятности появления события А в каждом испытании, т. е. М(Х) = пр.

Действительно, общее число Х появлений события А в п испытаниях складывается из числа появлений события в отдельных испытаниях X_i, , т.е. . Причем .

Поскольку математическое ожидание случайной величины X_i равно , то по свойству 4^о математического ожидания , получим: .

Дисперсия числа появлений события А в п независимых испытаниях, т, е. случайной величины X, распределенной по биномиальному закону, равна числу испытаний, умноженному на вероятности появления р и непоявления q события А в отдельном испытании, т.е. D(Х) = прq .

Докажем это. Как было показано выше, , . В силу свойства 3° дисперсии . Применим теорему 2.5 . Так как , то для вычисления найдем . Случайная величина принимает значение либо 1² (событие А произошло в i-м испытании) с вероятностью р, либо 0² (событие А не произошло вi-м испытании) с вероятностью q= 1 – р. Поэтому . Тогда и , что и требовалось доказать.

Пример 2.9.Пусть из большой партии изделий в целях контроля качества производится случайная выборка тридцати изделий с возвращением. Вероятность обнаружения брака р = 0,05. Вычислить вероятность того, что в случайной выборке: 1) нет бракованных изделий; 2) ровно 5 бракованных изделий.

Решение. Пусть Х – число бракованных изделий в выборке. Множество возможных значений случайной величины X: ; 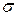-алгебру числового множества образуют любые подмножества , в том числе и одноточечные: . Вероятности определим на элементарных событиях по формуле Бернулли: .

Пусть событие А состоит в том, что в выборке нет бракованных изделий, , а событие В состоит в том, что в выборке ровно 5 бракованных изделий, В= {5}. Их вероятности вычислим по формуле (2.11):

Ответ:вероятность того, что в случайной выборке: 1) нет бракованных изделий, равна 0,215; 2) ровно 5 бракованных изделий – 0,012.

Пример 2.10. Из партии изделий, изготовленных автоматом, для контроля качества производится случайная выборка 1000 изделий с возвращением. Пусть из эксперимента известно, что средний процент брака для данного автомата составляет 1%. Какова вероятность того, что среди 1000 отобранных изделий будет не более 3 дефектных?

Решение. Пусть случайная величина Х – число дефектных изделий. Множество ее возможных значений . 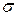-алгебру образуют все возможные подмножества числового множества . Вероятности событий определим по формуле (1.11). Пусть событие А состоит в том, что среди отобранных изделий не более 3 дефектных, А = {0,1,2,3}, Так р=0,01, п=1000, то вероятность события А

Ответ:вероятность того, что среди 1000 отобранных изделий будет не более 3 дефектных, равна

Из рассмотренного примера видно, что подсчет вероятностей по формуле Бернулли сопряжен в некоторых случаях с техническими трудностями. Поэтому необходимо получить приближенные формулы.

Наивероятнейшее число появления события в независимых испытаниях.Для получения приближенных формул вычисления вероятности появления события в независимых испытаниях исследуем изменение вероятностей при различных значениях т. Рассмотрим отношение

Тогда, если:

а) , т.е. , то ;

б) , то ;

в) , то .

Таким образом, вероятность с ростом т вначале увеличивается, достигая максимума при некотором значении , а затем убывает. При этом, если np–q – целое число, то вероятность Р_n (т) достигает максимума при двух значениях т: , и называемых наивероятнейшими значениями. Если же пр – q — не целое число, то наивероятнейшее значение одно, и оно удовлетворяет неравенству

пр - q < т₀ < nр+p,

так как вероятность максимальна при двух значениях т: т и т +1, те т т₀ т+1. Объединяя это неравенство с равенствами, приведенными выше, получаем формулу

,

по которой определяется наивероятнейшее число появления события в п независимых испытаниях.

Распределение Пуассона как предельное для биномиального. Как видно из примера 2.10, применение формулы Бернулли при малых р и больших п затруднительно. Однако значительный круг задач связан с необходимостью вычисления вероятностей Р_п(т) именно при малых значениях р и больших п. Поэтому возникает задача отыскания асимптотической формулы, специально приспособленной для малых значений р. Такая формула была выведена Пуассоном.

Теорема 2.6. Если вероятность р появления события в каждом испытании, при неограниченном увеличении числа испытаний п, изменяется таким образом, что пр = а, а= соnst, то вероятность того, что некоторое событие появится т раз в п испытаниях стремится к величине

, т.е. при .

Доказательство. По формуле Бернулли

Так как при , а

(α и т фиксированы), то , что и требовалось доказать.

Из теоремы следует, что для больших т и п справедливо равенство:

(2.12)

Предельную теорему Пуассона (формула (2.12)) используют, если р мало, а . Для удобства применения этой формулы составлены таблицы значений функции . Легко проверить, что . Действительно, , так как ряд является экспоненциальным.

Рассмотрим далее дискретную случайную величину Х – число наступлений •бытия А в п независимых испытаниях, которая принимает значения 0, 1, …, т, … с вероятностями .

В этом случае говорят, что случайная величина Х распределена по закону Пуассона и, следовательно, ее ряд распределения имеет вид, представленный следующей таблицей:

				…	т	…
				…		…

Как было показано выше, сумма вероятностей этого ряда распределения

равна 1. Функция пуассоновского распределения имеет вид

;

Найдем числовые характеристики случайной величины Х. По определению математического ожидания

Таким образом, математическое ожидание числа появлений события А в п независимых испытаниях (случайная величина X) равно пр , а это параметр а. Дисперсия, согласно теореме 2.5,

Дисперсия случайной величины, распределенной по закону Пуассона, равна ее математическому ожиданию.

Асимметрия и эксцесс, как легко показать, соответственно равны: , откуда следует, что они всегда положительны.

Пример 2.11. В тесто, приготовленное для выпечки 1000 булочек, засыпают 10000 изюминок и тщательно перемешивают. Какова вероятность того, что в случайно выбранной булочке будет: 1) 5 изюминок; 2) меньше 10 изюминок?

Решение. Пусть Х – число изюминок, попавших в булочку. Множество возможных значений случайной величины X: . В результате тщательного перемешивания каждая изюминка с одинаковой вероятностью может попасть в любую из 1000 булочек. Следовательно, вероятность того, что определенная изюминка попадает в выбранную булочку, равна 0,001. Число изюминок, попавших в выбранную булочку, можно рассматривать как результат п = 10 000 испытаний, в каждом из которых определенная изюминка с вероятностью р = 0,001 попадет в выбранную булочку. Так как пр = 10, то по теореме 2.6 вероятность события А = 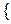число изюминок в случайно выбранной булочке равна 5 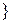, будет равна:

.

Вероятность события В = 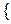число изюминок в случайно выбранной булочке меньше 10 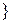, вычислим, используя формулу (2.12)

.

Ответ:вероятность того, что в случайно выбранной булочке будет: 1) 5 изюминок, равна 0,038; 2) меньше 10 изюминок – 0,46.

Примерами случайных величин, подчиняющихся закону распределения Пуассона, могут служить:

- количество распадающихся за короткий промежуток времени атомов радиоактивного вещества;

- число обрывов нити определенного сорта пряжи в течение времени Т;

- число дефектов в куске ткани определенной длины;

- число зафиксированных за определенный период времени метеоритов и т. д.

Простейший поток событий и его математическая модель. Формулу (2.12) можно считать математической моделью простейшего потока событий.

Введем некоторые определения.

Определение 2.15. Потоком событий называется последовательность событий, которые наступают в случайные моменты времени.

Например, поступление вызовов на станцию "Скорой помощи", моменты прибытия судов в порты, и т.д