Условная вероятность и ее свойства

Пусть áW, F, Pñ – математическая модель вероятностного эксперимента. Это значит, что любое событие A Í имеет определенную вероятность P(A), 0 £ P(A) £ 1. Вероятность события A связана с комплексом условий s рассматриваемого эксперимента. Как правило, вероятность события меняет свою величину с изменением комплекса условий s.

Пример 1.7. Пусть эксперимент состоит в бросании шестигранной игральной кости и подсчете выпавших очков 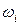. Пространство элементарных событий 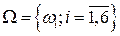, данного эксперимента, cостоит из шести элементарных событий: 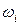= {игральная кость выпала гранью вверх содержащей 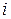очков}, 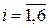. Пусть событие А = {выпадет число очков больше трех}: 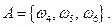Вероятность этого события, согласно формуле (1.2), равна 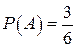. Предположим теперь, что об исходе эксперимента известно, что произошло событие В, стоящее в том, что выпало четное число очков: 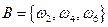. Вероятность события А в этом случае изменится. Событие В состоит из трех элементарных событий, при появлении двух из которых наступает событие А. Произошло сужение пространства до подмножества В и вероятность события А станет равной , в силу той же формулы (1.2).

Тот факт, что событие B наступило при условии, что событие A произошло, будем обозначать 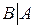и читать: "Событие B наступило при условии, что событие A произошло". Вероятность наступления события 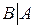обозначают 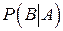и называют условной вероятностью наступления события B при условии, что событие A произошло.

Вероятность, равную 2/3, можно получить, если рассматривать отношение вероятностей события АВ и события В:

.

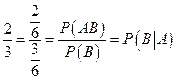Рассмотрим общий случай. Пусть пространство 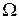состоит из n равновозможных элементарных событий. Событие А состоит из m элементарных событий, а событие В – из k элементарных событий. Причем события А и В, вообще говоря, совместны, т. е. событие АВ содержит r элементарных событий. Тогда вероятность события А при условии, что произошло событие В, определяется как и выше, т. е. 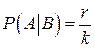. Полученное отношение 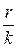равно отношению вероятностей событий АВ и В, так как 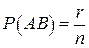, а :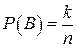

.

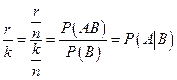Пример 1.8. Пусть пространство 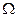вероятностного эксперимента состоит из несчетного множества элементарных событий 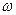, где 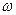= {выбор точки множества 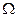евклидова пространства 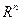, 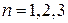}. События А и В состоят в том , что случайным образом выбирается точка, принадлежащая областям А и В соответственно.

Предположим, что событие В произошло, т. е. известно, что случайным образом выбрана точка, принадлежащая области В, и, следовательно, рассматриваются точки области В. В этом случае событие А наступит, если случайным образом выбрана точка из области АВ ( рис. 1. 4).

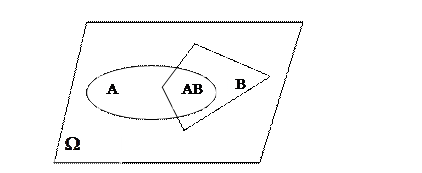
Рис.1.4

Вероятность события А при условии, что событие В имело место, согласно геометрическому методу задания вероятностей, вычисляется по формуле:

Эту же вероятность можно вычислить через вероятности событий АВ и В, так как 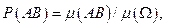а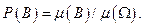

Определение 1.5. Пусть задано вероятностное пространство áW, F, Pñ и пусть A и B - произвольные события, A Í F, B Í F. Если P(B) > 0, то условной вероятностью события A при условии, что произошло событие B, называется число 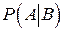, определяемое по формуле

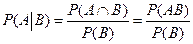. (1.7)

(Если P(B) = 0, то условная вероятность не определяется).

Точно так же определяется условная вероятность события B в предположении наступления события A:

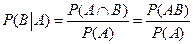. (1.8)

Условная вероятность обладает всеми свойствами вероятности.

1. Для любого события A условная вероятность удовлетворяет неравенству 0 £ P(A/B) £ 1.

Действительно, 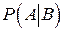= P(AB)/P(B), а P(AB) ³ 0, P(B) > 0 и P(AB) £

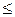P(B).

2. Если событие B влечет за собой событие A, то есть B Ì A, то P(A/B) = 1.

Действительно, если BÌA, то AB = B и P(AB) = P(B), = = .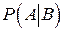

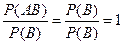3. Если события A и C несовместны, то .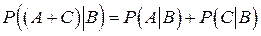

Действительно,

=

= .

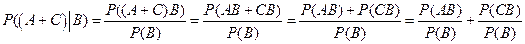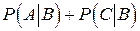Более того, если события A₁, A₂, ... – попарно несовместны, то

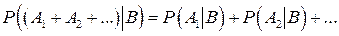
4. .

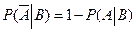Действительно, .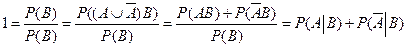

Откуда .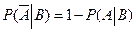

Таким образом, вероятностное пространство для условных вероятностей задается тройкой áB, FB, P(AB)/P(B)ñ. Это новое пространство построено с учетом добавочной информации об эксперименте, состоящей в том, что событие B наступило и, следовательно, произошло сужение пространства W. Новая s-алгебра FB пространства B строится пересечением событий из F с B. Если никаких ограничений на эксперимент, кроме условий 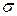, при вычислении вероятности 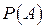не налагается, то такие вероятности называют безусловными.

Вопросы для самопроверки

1.Как определяется условная вероятность события В в предположении наступления события А?

2.В каких пределах заключается условная вероятность любого события?

3.Каким свойствам удовлетворяет условная вероятность?

4.Чему равна сумма условных вероятностей несовместных событий?

5. Как изменяется вероятностное пространство для условных вероятностей?