Тема: Интегрирование заменой переменной и по частям в неопределенном интеграле
Цель: Формирование навыков нахождения неопределенных интегралов методами замены переменной и по частям
Время выполнения: 2 часа
Требования к выполнению практической работы:
1.Ответить на теоретические вопросы.
2.Оформить задания в тетради для практических работ.
Теоретический материал
Проинтегрировать функцию 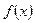 - значит найти ее неопределенный интеграл. Непосредственное интегрирование основано на прямом использовании основных свойств неопределенного интеграла и таблицы простейших интегралов.
- значит найти ее неопределенный интеграл. Непосредственное интегрирование основано на прямом использовании основных свойств неопределенного интеграла и таблицы простейших интегралов.
В основе интегрирования способом подстановки (или замены переменной) лежит свойство инвариантности формул интегрирования, которое заключается в следующем: если 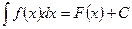 , то
, то 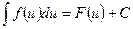 , где
, где 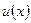 - произвольная дифференцируемая функция от
- произвольная дифференцируемая функция от 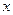 .
.
Замена переменной в неопределенном интеграле производится с помощью подстановок следующих двух типов:
1) 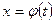 - где
- где 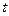 - новая переменная, а
- новая переменная, а 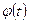 - непрерывно дифференцируемая функция. В этом случае формула замены переменной такова:
- непрерывно дифференцируемая функция. В этом случае формула замены переменной такова:
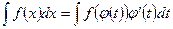 (14.1)
(14.1)
Функцию 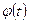 стараются выбирать таким образом, чтобы правая часть формулы (1) приобрела более удобный для интегрирования вид;
стараются выбирать таким образом, чтобы правая часть формулы (1) приобрела более удобный для интегрирования вид;
2) 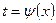 , где
, где 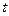 - новая переменная. В этом случае формула замены переменной имеет вид
- новая переменная. В этом случае формула замены переменной имеет вид
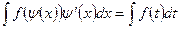 (14.2)
(14.2)
Интегрированием по частям называется нахождение интеграла по формуле
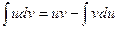 , (14.3)
, (14.3)
где 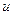 и
и 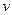 - непрерывно дифференцируемые функции от
- непрерывно дифференцируемые функции от 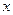 . С помощью формулы (14.3) отыскание интеграла
. С помощью формулы (14.3) отыскание интеграла 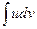 сводится к нахождению другого интеграла
сводится к нахождению другого интеграла 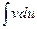 , ее применение целесообразно в тех случаях, когда последний интеграл либо проще исходного, либо ему подобен.
, ее применение целесообразно в тех случаях, когда последний интеграл либо проще исходного, либо ему подобен.
При этом в качестве 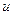 берется функция, которая при дифференцировании упрощается, а в качестве
берется функция, которая при дифференцировании упрощается, а в качестве 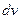 - та часть подынтегрального выражения, интеграл от которой известен или может быть найден.
- та часть подынтегрального выражения, интеграл от которой известен или может быть найден.
Так, при нахождении интегралов вида
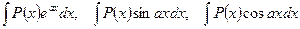 (14.4)
(14.4)
за 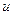 следует принять многочлен
следует принять многочлен 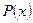 , а за
, а за 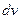 - соответственно выражения
- соответственно выражения 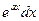 ,
, 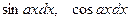 ; при отыскании интегралов вида
; при отыскании интегралов вида
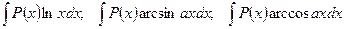 (14.5)
(14.5)
за 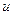 принимаются соответственно функции
принимаются соответственно функции 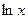 ,
, 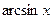 ,
, 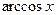 , а за
, а за 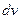 - выражение
- выражение 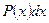 .
.
Примеры
Найти интегралы: 1) 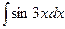 ; 2)
; 2) 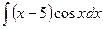 .
.
Решение: 1) Данный интеграл окажется табличным, если под знаком дифференциала будет находиться аргумент 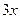 подынтегральной функции
подынтегральной функции 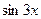 . Так как
. Так как 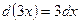 , то
, то 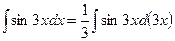 . Следовательно, подстановка
. Следовательно, подстановка 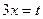 приводит рассматриваемый интеграл к табличному:
приводит рассматриваемый интеграл к табличному: 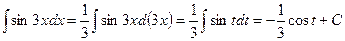 . Возвращаясь к старой переменной
. Возвращаясь к старой переменной 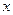 , окончательно получим
, окончательно получим 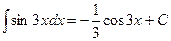 .
.
2) Предполагая 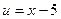 ,
, 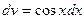 , найдем
, найдем 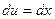 ,
, 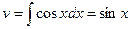 . Следовательно,
. Следовательно, 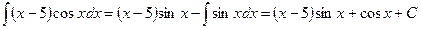 .
.
Задания для практической работы
1. Найдите интегралы методом непосредственного интегрирования:
1) 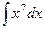 ; 2)
; 2) 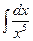 ;
;
3) 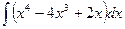 ; 4)
; 4) 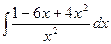 ;
;
5) 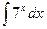 ; 6)
; 6) 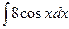 .
.
2. Найдите интегралы способом подстановки:
1) 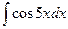 ; 2)
; 2)  ; 3)
; 3) 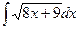 ; 4)
; 4) 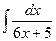 ; 5)
; 5) 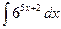 ; 6)
; 6) 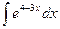 .
.
3. Найдите интегралы при помощи интегрирования по частям:
1) 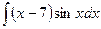 ; 2)
; 2) 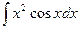 ; 3)
; 3) 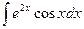 ; 4)
; 4) 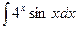 .
.
Контрольные вопросы:
1. Что называется первообразной? Перечислите свойства первообразной функции.
2. Что называется неопределенным интегралом?
3. Какие свойства неопределенного интеграла вы знаете?
4. Перечислите основные формулы интегрирования.
5. Какие методы интегрирования вы знаете? В чем заключается их сущность?
Рекомендуемая литература: 11.1[с. 271-282], 1.2[с. 205-212], 1.3[с. 52-62], 2.2[с. 247-250].
Практическая работа №15
