Тема: Составление уравнений прямых, их построение
Цель: Формирование навыков составления уравнений прямых, их построения
Время выполнения: 2 часа.
Требования к выполнению практической работы:
1.Ответить на теоретические вопросы.
2.Оформить задания в тетради для практических работ.
Теоретический материал
Уравнение первой степени относительно переменных 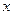 и
и 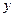 , то есть уравнение вида
, то есть уравнение вида 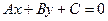 при условии, что коэффициенты
при условии, что коэффициенты 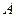 и
и 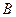 одновременно не равны нулю, называется общим уравнением прямой.
одновременно не равны нулю, называется общим уравнением прямой.
Уравнение вида 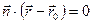 называется векторным уравнением прямой. Если его переписать в координатной форме, то получится уравнение
называется векторным уравнением прямой. Если его переписать в координатной форме, то получится уравнение 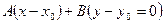 .
.
Каноническое уравнение прямой записывается в следующем виде 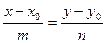 , где
, где  и
и 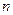 - координаты направляющего вектора прямой.
- координаты направляющего вектора прямой.
Уравнение прямой в отрезках на осях имеет вид 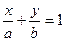 , где
, где 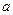 и
и 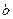 - соответственно абсцисса, и ордината точек пересечения прямой с осями
- соответственно абсцисса, и ордината точек пересечения прямой с осями 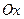 и
и 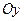 .
.
Уравнение прямой с угловым коэффициентом имеет вид 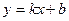 , где
, где 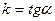 - угловой коэффициент, равный тангенсу угла наклона прямой к оси
- угловой коэффициент, равный тангенсу угла наклона прямой к оси 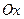 , а
, а 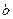 - ордината точки пересечения прямой с осью
- ордината точки пересечения прямой с осью 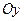 .
.
Уравнение прямой, проходящей через данную точку 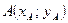 в заданном направлении, имеет вид
в заданном направлении, имеет вид 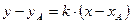 , где
, где 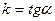 - угловой коэффициент прямой.
- угловой коэффициент прямой.
Уравнение прямой, проходящей через две данные точки 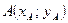 и
и 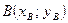 , имеет вид
, имеет вид 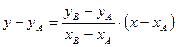 . Угловой коэффициент прямой, проходящей через точки
. Угловой коэффициент прямой, проходящей через точки 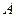 и
и 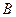 , находится из соотношения
, находится из соотношения 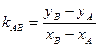 .
.
Пример
Задание 1: Построить прямую 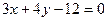 .
.
Решение: Найдем точки пересечения прямой с осями 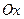 и
и 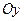 .
.
Пусть 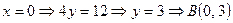 .
.
Пусть 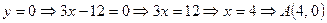 .
.
Изобразим найденные точки на координатной плоскости и соединим их, таким образом, получим прямую заданную уравнением 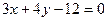 (рис. 1).
(рис. 1).
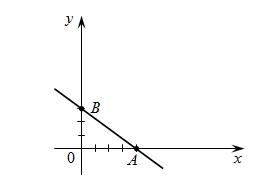
Рисунок 1 - График прямой 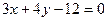
Задание 2: Построить прямую 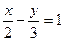 .
.
Решение: Перепишем уравнение в виде: 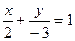 , то есть
, то есть 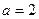 и
и 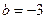 . Таким образом, получаем точки
. Таким образом, получаем точки 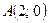 и
и 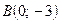 , прямая проходящая через точки
, прямая проходящая через точки 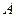 и
и 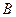 является искомой (рис. 2).
является искомой (рис. 2).
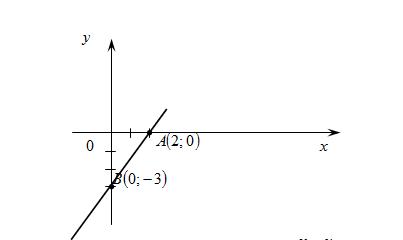
Рисунок 2 - График прямой 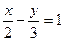 .
.
Задание 3: Составить уравнение прямой, проходящей через начало координат и точку 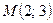 .
.
Решение: Вектор 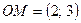 коллинеарен искомой прямой. Для составления уравнения прямой используем каноническое уравнение прямой:
коллинеарен искомой прямой. Для составления уравнения прямой используем каноническое уравнение прямой: 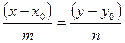 . Таким образом, подставив в данное уравнение
. Таким образом, подставив в данное уравнение 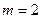 ,
, 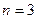 ,
, 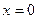 ,
, 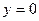 получим искомое уравнение прямой проходящей через начало координат и точку
получим искомое уравнение прямой проходящей через начало координат и точку 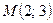 :
:
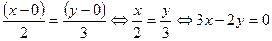 .
.
Задание 4: Составить уравнение прямой, проходящей через данную точку 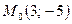 и перпендикулярной данному вектору
и перпендикулярной данному вектору 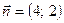 .
.
Решение: Пусть 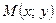 - произвольная точка искомой прямой. Вектор
- произвольная точка искомой прямой. Вектор 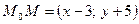 перпендикулярен вектору
перпендикулярен вектору 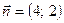 . Так как векторы перпендикулярны, то их скалярное произведение равно нулю, то есть
. Так как векторы перпендикулярны, то их скалярное произведение равно нулю, то есть 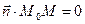 . Записав произведение этих векторов в координатной форме, получим:
. Записав произведение этих векторов в координатной форме, получим:
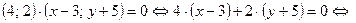
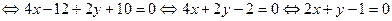 .
.
Уравнение искомой прямой имеет вид 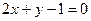 .
.
Задания для практической работы
1. Проверьте, принадлежат ли точки 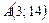 ,
, 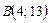 ,
, 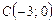 и
и 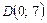 прямой
прямой 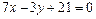 .
.
2. Постройте фигуру, ограниченную линиями 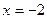 ,
, 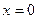 ,
, 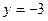 и
и 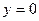 . Вычислите площадь этой фигуры.
. Вычислите площадь этой фигуры.
3. Преобразуйте уравнения следующих прямых к уравнениям в отрезках на осях и постройте данные прямые:
1) 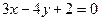 ; 2)
; 2) 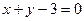 ;
;
3) 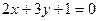 ; 4)
; 4) 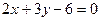 .
.
3. Составьте уравнение прямой, проходящей через начало координат и точку 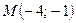 .
.
4. Составьте уравнение прямой, проходящей через данную точку 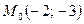 и перпендикулярной данному вектору
и перпендикулярной данному вектору 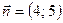 .
.
5. Составьте уравнение прямой, перпендикулярной вектору 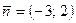 и проходящей через точку пересечения прямых
и проходящей через точку пересечения прямых 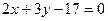 и
и 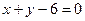 .
.
6. Составьте уравнение прямой, проходящей через точку пересечения прямых 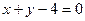 и
и 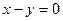 параллельно прямой
параллельно прямой 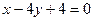 .
.
7. Даны координаты вершин треугольника 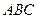 :
: 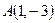 ,
, 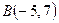 ,
, 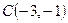 . Запишите уравнения прямых, на которых расположены:
. Запишите уравнения прямых, на которых расположены:
а) медиана 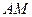 ;
;
б) высота 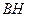 этого треугольника.
этого треугольника.
8. В треугольнике 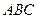 из вершины
из вершины 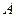 проведены высота и медиана (рис. 3). Даны: вершина
проведены высота и медиана (рис. 3). Даны: вершина 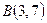 , уравнение высоты
, уравнение высоты 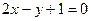 и уравнение медианы
и уравнение медианы 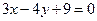 . Найти координаты вершины
. Найти координаты вершины 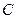 .
.
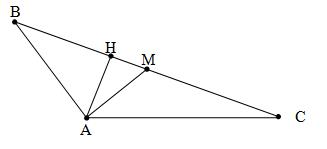
Рисунок 3 - Треугольник 
Контрольные вопросы:
1. Какое уравнение называется общим уравнением прямой?
2. Какой вид имеет векторное уравнение прямой?
3. Какое уравнение называется каноническим уравнением прямой?
4. Запишите уравнение прямой в отрезках на осях и уравнение прямой с угловым коэффициентом.
5. Какой вид имеют уравнения прямой, проходящей через данную точку в заданном направлении и прямой, проходящей через две данные точки?
6. Запишите условие параллельности двух прямых.
7. Запишите условие перпендикулярности двух прямых.
Рекомендуемая литература: 1.1[с. 300-308], 1.2[с. 304-326], 1.3[с. 52-62], 2.1[с. 6-15].
Практическая работа №7
