Критерии оценки практических работ

Для оценки качества успеваемости обучающихся большое значение имеет проверка выполнения ими практических работ. Практическая работа обучающегося позволяет преподавателю определить отношение обучающегося к учебной деятельности, качество усвоения изучаемого материала, наличие пробелов в знаниях, а также степень самостоятельности при выполнении работ.

Наибольший рейтинговый балл, который может заработать обучающийся, определяется приложением к рабочей программе «Рейтинговая система оценки», который доводится до обучающегося в начале семестра.

По итогам изученной дисциплины обучающийся может получить оценку согласно шкале (на основании Положения о рейтинговой системе оценки успеваемости студентов, обучающихся по программам СПО Тюменского государственного нефтегазового университета, 2013 г.):

от 88 до 100 баллов – «отлично»;

от 76 до 87 баллов – «хорошо»;

от 61 до 75 баллов – «удовлетворительно»;

60 баллов и менее – «неудовлетворительно».

Практическая работа №1

Тема: Операции над матрицами. Вычисление определителей

Цель: Формирование навыков выполнения операций над матрицами и вычисления определителей второго, третьего и четвертого порядков.

Время выполнения: 2 часа.

Требования к выполнению практической работы:

1. Ответить на теоретические вопросы.

2. Оформить задания в тетради для практических работ.

Теоретический материал

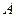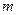Прямоугольная матрица размера ( - матрица) имеет вид таблицы (1.1), состоящей из строк и 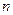столбцов:

(1.1)

Элемент матрицы 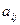находится на пересечении -ой строки и -го столбца, ; .

У нулевой матрицы 0 (1.2) все элементы равны нулю:

(1.2)

Матрица – столбец ( -матрица) (1.3) состоит из одного столбца:

, (1.3)

а матрица – строка ( -матрица) (1.4) из одной строки:

. (1.4)

Произведением двух матриц 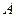и 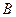называется матрица 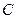, каждый элемент которой определяется по правилу строка на столбец, то есть элемент стоки матрицы 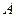умножается на элемент столбца матрицы 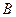стоящие на соответствующих местах.

Из определения произведения матриц следует, что не любые две матрицы можно перемножать. Произведение имеет смысл только тогда, когда число столбцов первой матрицы-сомножителя равно числу строк второй матрицы-сомножителя, что символически записывается так:

. (1.5)

Транспонирование -матрицы заключается в замене строк столбцами, а столбцов – строками с теми же номерами:

(1.6)

Матрица размера называется суммой двух - матриц и , если каждый элемент матрицы 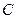равен сумме соответствующих элементов матриц 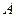и :

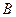. (1.7)

Определителем второго порядка называется число, определяемое равенством

. (1.8)

Числа называются элементами определителя; при этом элементы и образуют главную диагональ, а элементы и - побочную диагональ. Таким образом, определитель второго порядка равен произведению элементов главной диагонали минус произведение элементов побочной диагонали.

Определителем третьего порядка называется число, определяемое равенством

(1.9)

.

Таким образом, каждый член определителя третьего порядка представляет собой произведение трех его элементов, взятых по одному из каждой строки и каждого столбца. Эти произведения берутся с определенными знаками: со знаком «плюс» – члена, состоящие из элементов главной диагонали и из элементов, расположенных в вершинах треугольников с основаниями, параллельными главной диагонали; со знаком «минус» – три члена, расположенные аналогичным образом относительно побочной диагонали.

Указанное правило называется правилом треугольников (Саррюса).

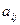Минором элемента называется определитель , полученный из вычеркиванием -ой строки и -го столбца.

Алгебраическим дополнением 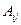элемента 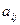называется его минор, умноженный на :

. (1.10)

Определитель 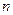-го порядка равен сумме произведений элементов какой – либо строки или столбца на их алгебраические дополнения:

(1.11)

(разложение определителя по элементам -ой строки) или

(1.12)

(разложение определителя по элементам -го столбца).

В частности, для определителя третьего порядка имеем

,

что совпадает с результатом, полученным по формуле (1.13).

Примеры

Задание 1: Найти сумму и разность матриц

и .

Решение: Здесь даны матрицы одного размера , следовательно,

существуют их сумма и разность. Согласно определению

алгебраической суммы матриц имеем

, .

Задание 2: Вычислить определители: 1) ; 2) .

Решение: 1) По формуле (1.8) находим .

2) Разлагая данный определитель, например, по элементам первой строки, находим

.

Тот же результат получится, если воспользоваться формулой (1.9):

.

Задания для практической работы

1. Даны матрицы: , . Произведите указанные действия, а в случае, когда это невозможно, указать причину:

1) ; 2) .

2. Даны матрицы и . Найдите матрицу .

3. Найдите матрицу , если , , .

4. Дано произведение матриц . Укажите значения , , .

5. Решите матричное уравнение . Для найденного решения необходимо сделать проверку.

6. Дана матрица . Найдите матрицу .

7. Вычислите определители второго порядка:

а) ; б) ; в) .

8. Вычислите определители третьего порядка:

а) ; б) ; в) .

9. Вычислите определитель четвертого порядка путем его разложения по элементам любой строки или по элементам любого столбца

.

Контрольные вопросы:

1. Что называется матрицей? Как установить размеры матрицы?

2. Какая матрица называется квадратной, верхнетреугольной, нижнетреугольной, диагональной, единичной?

3. Назовите линейные операции над матрицами. Как они производятся?

4. Какие матрицы можно перемножать? Как это делается?

5. Какая диагональ матрицы называется главной, побочной?

6. Что называется определителем?

7. Как вычисляются определители второго и третьего порядков?

8. Как вычисляются определители 4, 5 и более высоких порядков?

9. Что называется минором и алгебраическим дополнением для произвольного элемента определителя?

Рекомендуемая литература: 1.2[с.7-10], 2.1[с.70-80].

Практическая работа №2