Лабораторная работа № 4. ИНТЕРПОЛИРОВАНИЕ

Системы функций Чебышева

Рассмотрим линейное множество 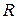действительных функций, определенных на отрезке 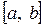, и некоторую конечную или счетную систему линейно независимых функций 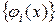из этого множества.

Линейную комбинацию

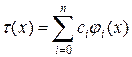
с действительными коэффициентами 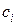называют обобщенным многочленом по системе функций .

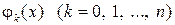Определение. Совокупность функций 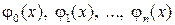называется системой Чебышева на отрезке 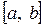, если любой обобщенный многочлен по этой системе, у которого хотя бы один из коэффициентов отличен от нуля, имеет на 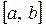не более корней.

Пусть на отрезке 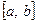в некоторых попарно различных точках 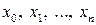известны значения функций .

Задача интерполирования функции состоит в том, чтобы найти значение 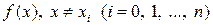, если известны узлы интерполирования 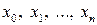и значения функции в этих узлах.

Решается задача интерполирования следующим образом: выбирается система функций 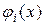, строится обобщенный многочлен 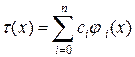, а коэффициенты 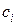задаются таким образом, чтобы в узлах интерполирования значения обобщенного многочлена совпадали со значениями данной функции :

.

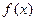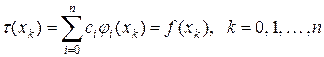Обобщенный многочлен, обладающий таким свойством, называется обобщенным интерполяционным многочленом. За приближенное значение принимают значение .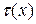

Выясним, когда задача интерполирования решается однозначно.

Теорема 1. Для того, чтобы для любой функции 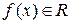, определенной на отрезке 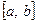, и любого набора 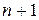узлов 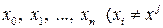при 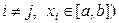существовал и был бы единственным обобщенный интерполяционный многочлен , необходимо и достаточно, чтобы система функций 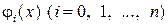являлась системой Чебышева на .

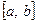На практике чаще всего используются следующие системы:

1)

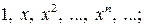
2)

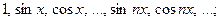
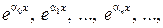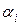3) где – некоторая числовая последовательность попарно различных действительных чисел.

В случае 1 интерполирование называется алгебраическим, в случае 2 – тригонометрическим (применяется для приближения 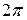– периодических функций), в случае 3 – экспоненциальным.

Метод Лагранжа

Пусть - набор различных точек (узлов) на отрезке , в котором заданы значения достаточно гладкой функции так, что , . Требуется построить многочлен степени не выше , принимающий в точках значения , и оценить погрешность приближения функции этим многочленом на всем отрезке .

Введем в явном виде вспомогательные многочлены степени , удовлетворяющие условиям по формулам:

. (4.1)

Тогда интерполяционный многочлен можно задать по формуле Лагранжа:

, (4.2)

при этом удобно преобразовать к виду:

, (4.3)

где .

Разность называется погрешностью интерполирования, или остаточным членом интерполирования. В узлах интерполирования погрешность обращается в нуль, в остальных точках она отлична от нуля, но если – многочлен степени , то . Если функция имеет непрерывную - ю производную, то остаточный член можно представить в виде

, (4.4)

где – некоторая точка, лежащая на отрезке, содержащем узлы и точку .

Пример 1. Построить многочлен наименьшей степени, принимающий в данных точках следующие значения:

х	– 1
y	– 14	– 5

По формуле (4.1) вычислим вспомогательные многочлены:

,

,

,

.

Затем по формуле (4.2) построим интерполяционный многочлен Лагранжа:

.