Систем линейных алгебраических уравнений

Методы решения систем линейных алгебраических уравнений (СЛАУ) можно разделить на две группы:

1) точные методы;

2) методы последовательных приближений.

С помощью точных методов, проделав конечное число операций, можно получить точные значения неизвестных. При этом предполагается, что коэффициенты и правые части системы известны точно, а все вычисления проводятся без округлений. Чаще всего решение задач такими методами осуществляется поэтапно. На первом этапе систему преобразуют к тому или иному простому виду, на втором – решают упрощенную систему и получают значения неизвестных.

Методы последовательных приближений характеризуются тем, что с самого начала решение задается какими-то приближенными значениями неизвестных, которые затем многократно улучшаются тем или иным способом.

Система m линейных уравнений с m неизвестными имеет вид:

(3.1)

где (i = 1, 2, ..., m; j = 1, 2, ..., m) – произвольные числа, называемые соответственно коэффициентами при переменных и свободными членами уравнений.

Система уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет решений.

3.1. Методы исключения неизвестных (метод Гаусса)

Наиболее распространенным методом решения СЛАУ является метод Гаусса, в основе которого лежит идея последовательного исключения неизвестных. С помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которой последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные.

Рассмотрим решение системы (3.1) m линейных уравнений с m неизвестными в общем виде.

Предположим, что в системе (3.1) (этого всегда можно добиться

перестановкой уравнений или переменных с изменением их номеров).

Метод Гаусса состоит в последовательном исключении неизвестных из этой системы.

Предположим, что . Последовательно умножая первое уравнение на и складывая с i-м уравнением, исключим из всех уравнений, кроме первого. Получим систему:

где , , .

Аналогичным образом из полученной системы исключим . Последовательно, исключая все неизвестные, получим систему треугольного вида:

Описанная процедура называется прямым ходом метода Гаусса. Ее выполнение возможно при условии, что все , ( ) не равны нулю.

Выполняя последовательные подстановки в последней системе (начиная с последнего уравнения), можно получить все значения неизвестных.

, .

Эта процедура получила название обратный ход метода Гаусса.

Блок-схема алгоритма решения СЛАУ методом Гаусса

Задание

Решить системы ЛАУ методом Гаусса.

Варианты заданий:

№ варианта	Система уравнений

3.3. Контрольные вопросы

1. К какому виду приводится матрица в методе Гаусса?

2. В каком случае нельзя применить метод Гаусса?

3. Что нужно предусмотреть при использовании метода Гаусса?

Итерационные методы

Метод называется приближенным, если при точном выполнении всех требуемых действий и при точных коэффициентах мы получаем, как правило, лишь приближенный результат.

Впрочем, практически и при применении точного метода результат оказывается приближенным по двум причинам: во-первых, коэффициенты уравнений обычно бывают приближенными числами; во-вторых, промежуточные вычисления на практике обычно невозможно выполнять с полной точностью. Значит, погрешность окончательного результата складывается из неустранимой погрешности задания исходных данных (коэффициентов) и погрешностей округления.

В случае применения приближенного метода на окончательный результат влияет всегда погрешность метода, также на практике обычно имеет место неустранимая погрешность в задании коэффициентов и погрешность округления в промежуточных действиях.

Одношаговый линейный стационарный итерационный процесс называется методом простой итерации (МПИ).

Пусть дана система ЛАУ с неособенной матрицей. В методе простой итерации ее предварительно приводят к виду:

.

Для очень больших систем, когда метод Гаусса становится неэффективным, применяют итерационные методы, например, метод простой итерации или метод Зейделя.

Метод простой итерации

Вычисления по методу простой итерации начинаются с произвольного вектора X⁰ ={x₁⁰, x₂⁰ , ... , x_n⁰}. Итерационный процесс осуществляется по формуле:

т. е. все неизвестные на следующей итерации вычисляются только через неизвестные на предыдущей итерации.

Условия завершения итерационного процесса:

d £ e (1)

где e – требуемая точность;

d – оценка достигнутой точности.

(2)

или

. (3)

Условие сходимости итерационного процесса (условие преобладания диагональных коэффициентов):

, (4)

Метод Зейделя

Метод Зейделя отличается от простой итерации тем, что найдя какое-то приближение для компоненты, мы сразу же используем его для отыскания следующей компоненты.

В методе Зейделя используется итерационная формула

,

в которой при вычислении очередного неизвестного используются последние найденные значения остальных неизвестных. Вычисления заканчиваются, когда невязки системы становятся достаточно малыми. Итерационные методы сходятся не для всякой матрицы. Достаточным условием сходимости является положительная определенность матриц.

Задание

Решить системы линейных алгебраических уравнений методами:

1) простой итерации;

2) метод Зейделя.

Варианты заданий:

№ варианта	Система уравнений	Точность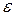

Контрольные вопросы

1. Чем отличаются точные методы от итерационных?

2. Как выбираются начальные приближения в методах простой итерации и Зейделя?

3. Каково условие прекращения итерации в методе простой итерации и в методе Зейделя для решения систем линейных алгебраических уравнений?