Расчет на прочность при сложном сопротивлении: плоском изгибе с растяжением (сжатием)

Сложным сопротивлением называются виды нагружения, при которых в поперечных сечениях одновременно действуют несколько внутренних силовых факторов.

Сложный вид деформации можно рассматривать как сумму простых видов, изученных ранее (растяжение, изгиб, кручение), при которых в сечениях элементов конструкций возникал только один внутренний силовой фактор: нормальная силаN – при растяжении, изгибающий момент М_Х – при чистом изгибе, крутящий момент М_КР – при кручении. Эти виды нагружения: растяжение, изгиб, кручение, являются простыми.

При движении звенья механизма испытывают сложное нагружение: плоский изгиб с растяжением (сжатием).

Растяжением (сжатием) называется такой вид нагружения, при котором в поперечных сечениях детали возникает только продольная (нормальная) сила N. При этом в отдельных точках сечения будет действовать только нормальное напряжение .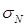

Экспериментально установлено, что при растяжении (сжатии) поперечные сечения стержня не искривляются и перемещаются параллельно друг другу, поэтому относительная продольная деформация во всех точках сечения одинакова и при упругом деформировании связана с напряжениями законом Гука. Следовательно, и напряжения во всех точках сечения постоянны.

Нормальное напряжение в i-том поперечном сечении определяется выражением:

,

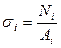где 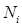– продольная сила, действующая в i-том сечении;

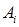– площадь i-го сечения стержня.

Плоский изгиб– такой вид нагружения, при котором все нагрузки лежат в одной плоскости (силовая плоскость), силы перпендикулярны оси стержня, а силовая плоскость совпадает с осью симметрии сечения. При плоском изгибе в поперечных сечениях стержня возникают два внутренних силовых фактора: изгибающий момент и поперечная сила – M_x и Q_y.

Различают два вида плоского изгиба:

а) поперечный, при котором поперечная сила не равна нулю;

б) чистый, при котором в поперечных сечения стержня возникает только один изгибающий момент (Q_y = 0).

В случае сложного сопротивления (плоском изгибе с растяжением или сжатием) условие прочности будет следующим:

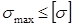, (3.10)

где 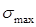– максимальное напряжение, возникающее в сечении детали и равное:

,

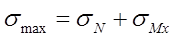где 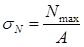– нормальное напряжение в опасном сечении, возникающее от действия продольной силы;

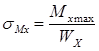– нормальное напряжение в опасном сечении, возникающее от действия изгибающего момента;

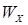– осевой момент сопротивления сечения детали.

Значения нормальной силы и изгибающего момента берутся из эпюр внутренних силовых факторов, которые строятся методом сечений.

Опасными точками в сечении (точки, в которых значение нормальных напряжений принимает максимальное значение) будут те, где знак напряжений от изгибающего момента совпадает со знаком напряжения от продольной силы. Следовательно, формула (3.10) примет вид:

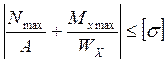. (3.11)

В полученном выражении первое слагаемое в левой части неравенства берется с учетом знака N, а второе – с таким же знаком, как и у N.

Пример №9. По данным примера №7 построить эпюры внутренних усилий для звена АВ.

Дано: , , , , , , , , , , .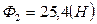

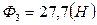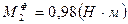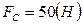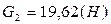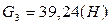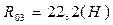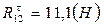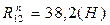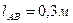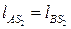Решение:

Для удобства построения эпюр повернем звено АВ в горизонтальное положение (рис. 3.11).

Рис.3.11. Звено АВ с приложенными силами

Методом сечений определяем законы изменения продольной силы N, поперечной силы Q_y и изгибающего момента M_x. Рассмотрим два силовых участка BS₂ и АS₂. На участке АС внутренние усилия равны нулю.

Участок 1.

Границы участка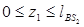

Рис. 3.12. Расчетная схема участка 1

Для определения внутренних усилий составим уравнения равновесия участка 1:

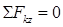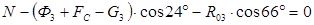; , откуда

,

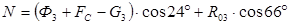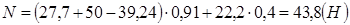, эпюра – const.

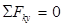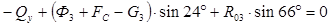; , откуда

,

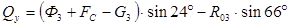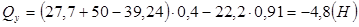, эпюра – const.

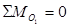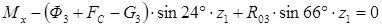; , откуда

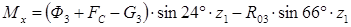, линейная зависимость, эпюра – наклонная прямая.

При ; ;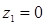

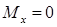При ; .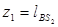

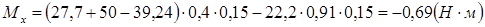Участок 2.

Границы участка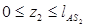

Рис. 3.13. Расчетная схема участка 2

Для определения внутренних усилий составим уравнения равновесия участка 1:

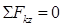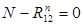; , откуда 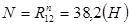,эпюра – const.

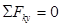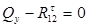; , откуда 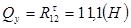, эпюра – const.

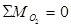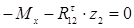; , откуда

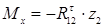, линейная зависимость, эпюра – наклонная прямая.

При ; ;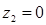

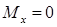При ; .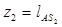

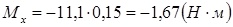Строим эпюры внутренних усилий (см. рис. 3.14).