VI. Решение уравнения теплопроводности для бесконечного стержня по формулам Пуассона
Пример 5.
Найти решение следующего уравнения теплопроводности с заданным начальным условием:
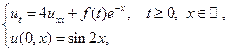
где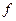 
– непрерывная при 
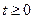функция.
Решение.
Решение данной задачи представимо в виде двух интегралов, один из которых учитывает начальное условие, а второй – влияние внутренних источников. Следовательно,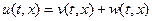 
, где 
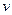и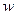 
находим по формулам Пуассона.
Для функции 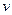справедливо следующее интегральное представление:
.
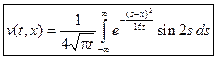Сделаем в интеграле замену переменных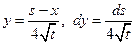 
:
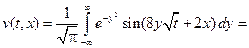
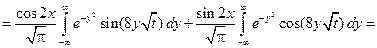
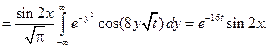
Применяем формулу для функции :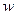
.
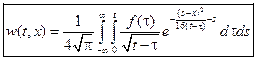Преобразуем показатель экспоненты, выделив полный квадрат по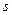 
:
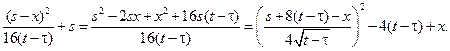Меняем порядок интегрирования, делаем замену переменных 
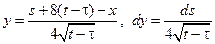и в итоге получаем:
.
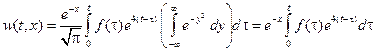Следовательно,
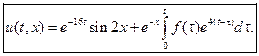
Задание 8.
Применяя формулы Пуассона, найти решения следующих уравнений теплопроводности для бесконечного стержня.
1. 
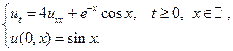
2. 
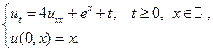
3. 
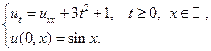
4. 
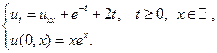
5. 
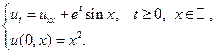
6. 
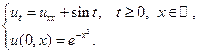
7. 
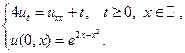
8. 
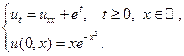
9. 
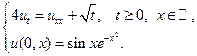
10. 
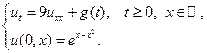
11. 
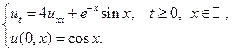
12. 
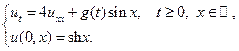
13. 
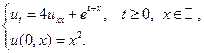
14. 
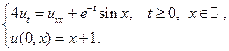
15. 
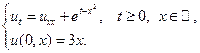
16. 
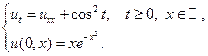
17. 
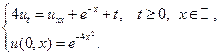
18. 
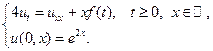
19. 
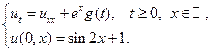
20. 
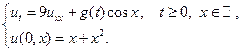
21. 
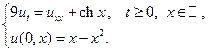
22. 
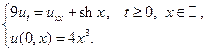
23. 
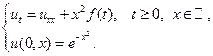
24. 
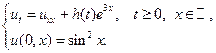
25. 
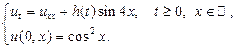
VII. Решение краевых задач для уравнений эллиптического типа. Прямоугольные и круговые области.
Пример 6.
Найти гармоническую в кольце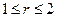 
функцию, удовлетворяющую краевым условиям: 
.
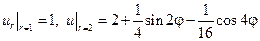Решение.
Пусть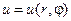 
– искомая функция. В силу определения гармонической функции, она является решением уравнения Лапласа с смешанными краевыми условиями на границах кольца:
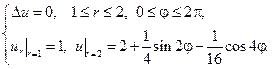
Используем представление решения уравнения Лапласа для кольца:
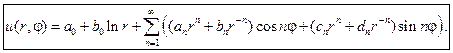Постоянные 
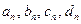найдем из граничных условий. Так как
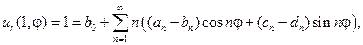
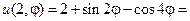
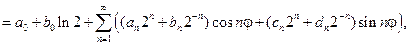
то, по формулам коэффициентов ряда Фурье, получаем:
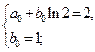
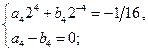
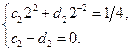
Все три системы однозначно разрешимы, из них находим: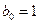 
, 
, 
, 
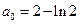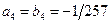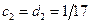. Далее, при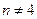 
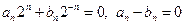, следовательно, 
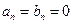; при 
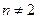
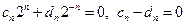, следовательно, 
.
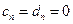Подставляя найденные коэффициенты в формулу представления решения, имеем окончательно:
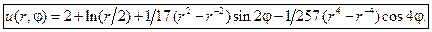
Задание 9.
Найти решения следующих краевых задач для уравнений Лапласа и Пуассона в заданных областях.
1. 
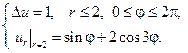
2. 
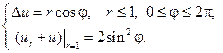
3. 
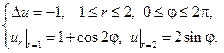
4. 
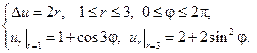
5. 
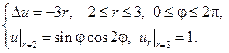
6. 
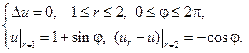
7. 
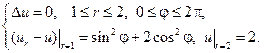
8. 
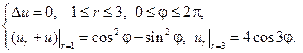
9. 
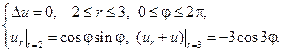
10. 
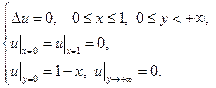
11. 
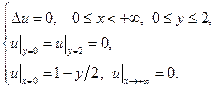
12. 
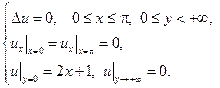
13. 
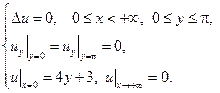
14. 
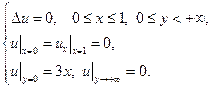
15. 
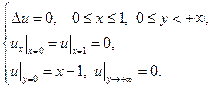
16. 
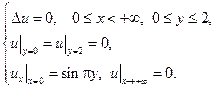
17. 
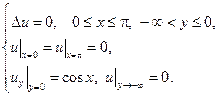
18. 
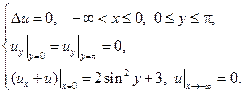
19. 
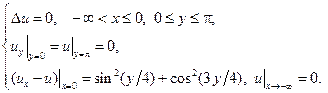
20. 
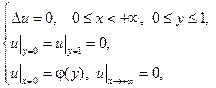
где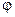 
– произвольная непрерывная функция.
21. 
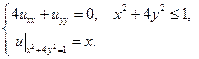
22. 
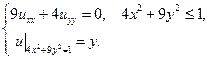
23. 
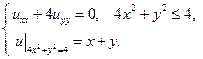
24. 
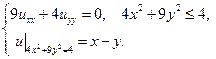
25. 
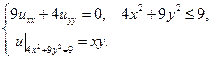
VIII. Решение вариационных задач на плоскости и в пространстве
Пример 6.
Найти экстремаль функционала
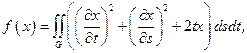(8.1)
где 
– единичный круг с центром в начале координат, с граничными условиями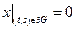 
.
Решение.
Как известно из курса вариационного исчисления, если функция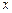 
– экстремаль функционала 
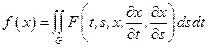, то она является решением уравнения Эйлера–Пуассона 
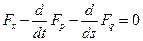, где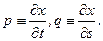 
Для функционала (8.1) 
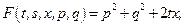следовательно,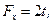 
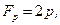
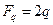, а уравнение Эйлера–Пуассона принимает вид:
,
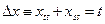то есть представляет собой уравнение эллиптического типа. Область, на которой ищется решение – внутренность круга (ограниченное множество), граница его – окружность, вдоль которой функция 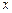обращается в нуль. Следовательно, искомая экстремаль является решением задачи Дирихле для внутренности круга.
Для круга естественно переформулировать задачу, перейдя к полярным координатам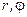 
. Пусть 
.
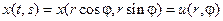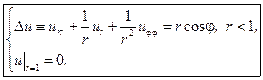(8.2)
Заменой переменных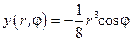 
сводим уравнение (8.2) к однородному (с ненулевыми граничными условиями):
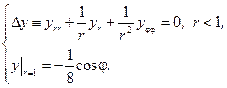(8.3)
Решение задачи (8.3) имеет представление в виде ряда:
.
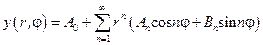Учитывая граничные условия, получаем:
,
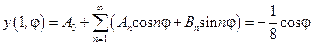откуда по формуле для коэффициентов ряда Фурье имеем:
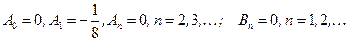. Следовательно, 
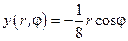, а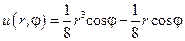 
. Возвращаясь к переменным 
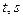и функции 
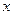, получаем решение уравнения Эйлера–Пуассона:
.
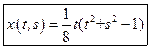Задание 10
Найти экстремали следующих функционалов в указанных областях с заданными условиями на границе.
1. 
,
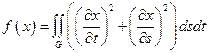– сектор круга: 
.
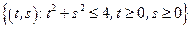Граничные условия: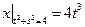 
, 
.
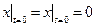2. 
,
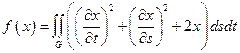– кольцо: 
.
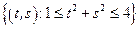Граничные условия: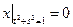 
, 
.
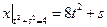3. 
,
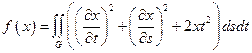– круг: 
.
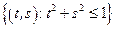Граничные условия: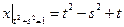 
.
4. ,
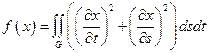– квадрат: 
.
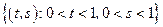Граничные условия: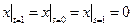 
, 
.
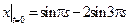5. ,
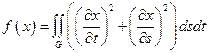– сектор кольца: 
.
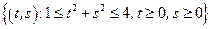Граничные условия: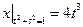 
, 
.
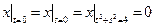6. ,
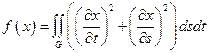– сектор круга: 
.
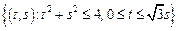Граничные условия: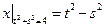 
, 
.
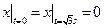7. 
,
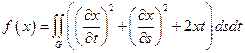– кольцо: 
.
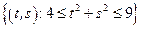Граничные условия: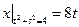 
, 
.
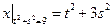8. 
,
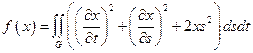– круг: 
.
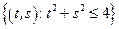Граничные условия: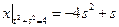 
.
9. ,
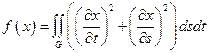– квадрат: .
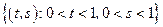Граничные условия: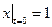 
, 
.
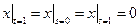10. 
,
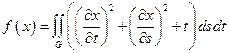– сектор кольца: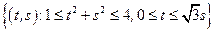 
.
Граничные условия: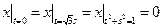 
, 
.
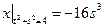11. 
,
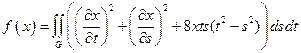– сектор круга: 
.
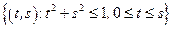Граничные условия: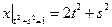 
, 
.
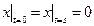12. 
,
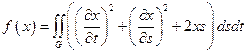– кольцо: 
.
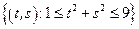Граничные условия: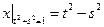 
, 
.
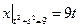13. ,
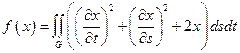– круг: 
.
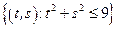Граничные условия: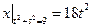 
.
14. 
,
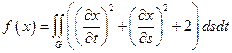– квадрат: .
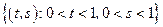Граничные условия: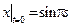 
, 
, 
.
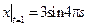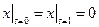15. 
,
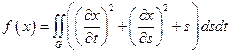– сектор кольца: 
.
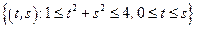Граничные условия: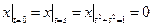 
, 
.
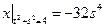16. ,
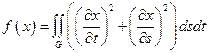– сектор круга: 
.
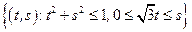Граничные условия: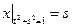 
, 
.
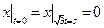17. 
,
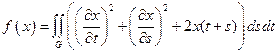– кольцо: .
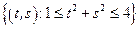Граничные условия: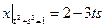 
, 
.
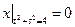18. 
,
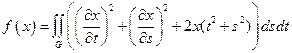– круг: .
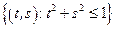Граничные условия: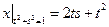 
.
19. ,
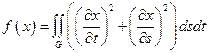– квадрат: .
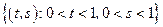Граничные условия: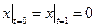 
, 
, 
.
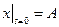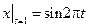20. 
,
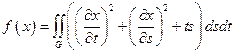– сектор кольца: .
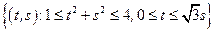Граничные условия: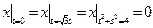 
, 
.
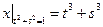21. ,
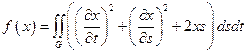– сектор круга: 
.
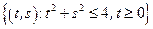Граничные условия: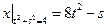 
, .
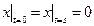22. 
,
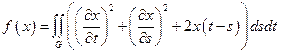– кольцо: .
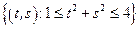Граничные условия: ,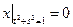 
.
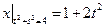23. 
,
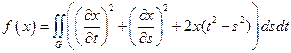– круг: .
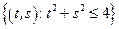Граничные условия: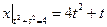 
.
24. ,
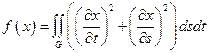– квадрат: .
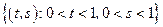Граничные условия: ,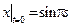 
, 
.
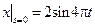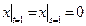25. ,
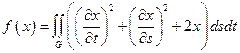– сектор кольца: 
.
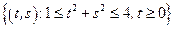Граничные условия: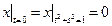 
, 
.
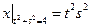Задание 11
Найти экстремали следующих функционалов в указанных областях с заданными условиями на границе, используя для построения решения функции Бесселя и многочлены Лежандра.
1. 
,
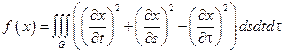– прямой круговой цилиндр: 
.
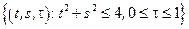Граничные условия: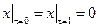 
, 
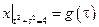, где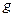 
– непрерывная на отрезке 
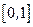функция.
2. 
,
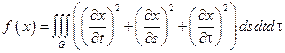– прямой круговой цилиндр: 
.
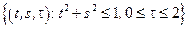Граничные условия: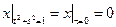 
, 
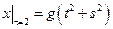, где 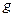– непрерывная на отрезке 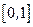функция.
3. ,
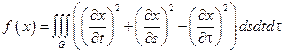– прямой круговой цилиндр: .
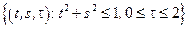Граничные условия: 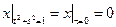, , 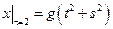где 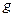– непрерывная на отрезке 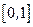функция.
4. ,
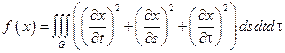– шар: 
.
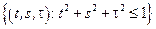Граничные условия: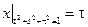 
.
5. ,
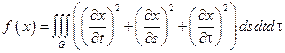– шар: 
.
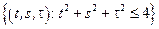Граничные условия: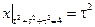 
.
6. ,
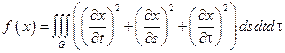– шар: .
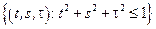Граничные условия: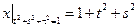 
.
7. ,
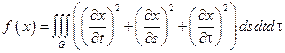– шар: .
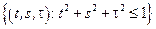Граничные условия: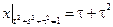 
.
8. ,
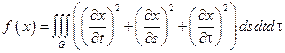– шар: .
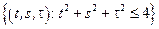Граничные условия: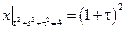 
.
9. 
,
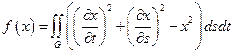– круг: .
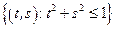Граничные условия: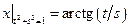 
.
10. 
,
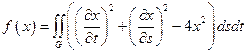– сектор круга: .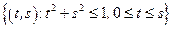
Граничные условия: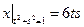 
, .
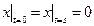11. 
,
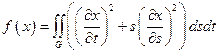– квадрат: .
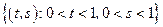Граничные условия: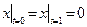 
, 
, 
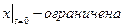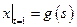, где 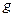– непрерывная на отрезке 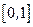функция.
12. 
,
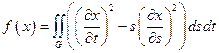– квадрат: .
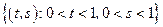Граничные условия: 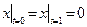, , 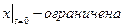, 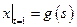где 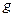– непрерывная на отрезке 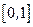функция.
13. ,
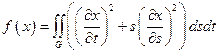– прямоугольник: 
.
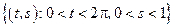Граничные условия: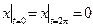 
, , 
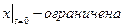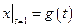, где 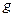– непрерывная на отрезке 
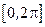функция.
14. ,
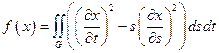– прямоугольник: .
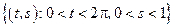Граничные условия: 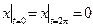, , 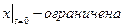, 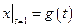где 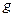– непрерывная на отрезке 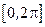функция.
15. 
,
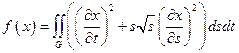– квадрат: .
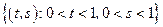Граничные условия: 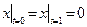, , 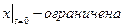, 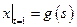где 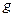– непрерывная на отрезке 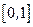функция.
16. 
,
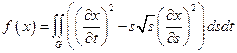– квадрат: .
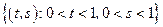Граничные условия: 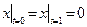, , 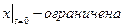, 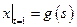где 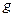– непрерывная на отрезке 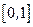функция.
17. ,
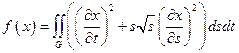– прямоугольник: .
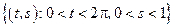Граничные условия: 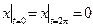, , 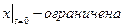, 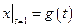где 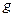– непрерывная на отрезке 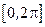функция.
18. ,
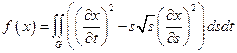– прямоугольник: .
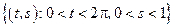Граничные условия: 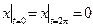, , 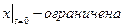, 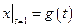где 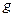– непрерывная на отрезке 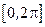функция.
19. 
,
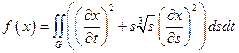– квадрат: .
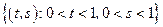Граничные условия: 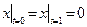, , 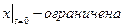, 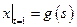где 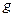– непрерывная на отрезке 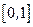функция.
20. 
,
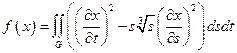– квадрат: .
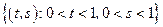Граничные условия: 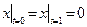, , 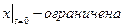, 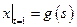где 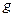– непрерывная на отрезке 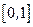функция.
21. ,
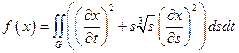– прямоугольник: .
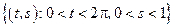Граничные условия: 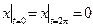, , 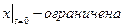, 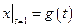где 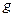– непрерывная на отрезке 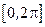функция.
22. ,
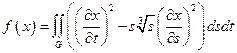– прямоугольник: .
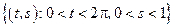Граничные условия: 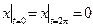, , 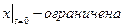, 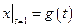где 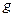– непрерывная на отрезке 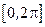функция.
23. 
,
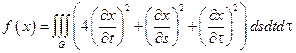– эллиптический цилиндр: 
.
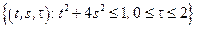Граничные условия: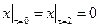 
, 
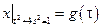, где 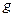– непрерывная на отрезке 
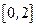функция.
24. 
,
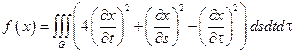– эллиптический цилиндр: 
.
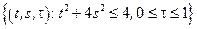Граничные условия: ,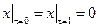 
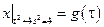, где 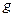– непрерывная на отрезке 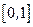функция.
25. ,
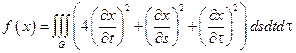– эллиптический цилиндр: .
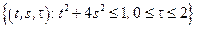Граничные условия: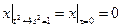 
, 
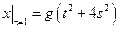, где 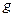– непрерывная на отрезке 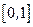функция.