Уравнения математической физики
Уравнения математической физики
Методические указания и индивидуальные задания
для самостоятельной работы студентов
III курса специальностей ВМ, БМ, ДПМ
Издательство
Пермского государственного технического университета
УДК 517 (075.8)
Уравнения математической физики: методические указания для самостоятельной работы студентов III курса / сост. доцент Малыгина В.В. – Пермь: Изд-во Перм. гос. техн. ун-та, 2016. –
В методических указаниях приводятся примеры решения задач из курса «Уравнения математической физики» и задачи для самостоятельного решения. Предполагается, что студенты владеют математическим аппаратом из разделов «Дифференциальное и интегральное исчисление» и «Дифференциальные уравнения».
Список рекомендуемой литературы по предмету приведен в конце указаний.
Рецензент:
кандидат физико-математических наук, доцент кафедры ВММ К.М.Чудинов
© ГОУВПО «Пермский
государственный технический
университет», 2016
Вводные замечания
Круг вопросов математической физики тесно связан с изучением различных физических процессов в таких областях науки и техники как механика, теплофизика, электричество, магнетизм, оптика и т.д. Возникающие при этом математические задачи (вывод которых опирается на механические или физические законы) содержат много общих элементов и составляют предмет математической физики. Большинство уравнений самой математической физики есть дифференциальные уравнения с частными производными. В отличие от обыкновенных дифференциальных уравнений, в которых неизвестная функция зависит только от одной переменной, в уравнениях с частными производными неизвестная функция зависит от нескольких переменных. Наиболее часто в приложениях встречаются дифференциальные уравнения в частных производных первого и второго порядка.
Данное пособие предназначено для студентов III курса, изучающих семестровый курс уравнений математической физики. Целью пособия является демонстрация основных методов решения простейших задач классической математической физики.
I. Линейные и квазилинейные уравнения в частных производных первого порядка
Пример 1.
Найти решение квазилинейного уравнения первого порядка, удовлетворяющее заданным условиям.
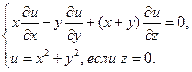
Решение.
Точки равновесия данного уравнения определяются из системы: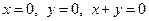 
, следовательно, множество точек равновесия – ось 
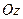и областью, в которой определено общее решение данного уравнения является множество 
.
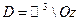Составим характеристическую систему
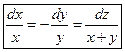
и найдем два линейно-независимых первых интеграла этой системы.
Так как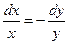 
, то 
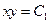– один первый интеграл. Далее, так как
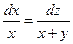, то 
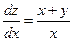или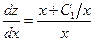 
, следовательно, 
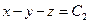– другой первый интеграл системы. Находим общее решение исходного уравнения:
,
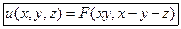где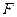 
– произвольная непрерывно дифференцируемая функция, 
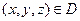. Любое частное решение получается из общего при конкретном выборе функции 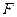. В нашем случае, из условий задачи имеем: 
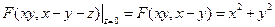. Обозначим 
, 
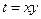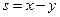. Так как 
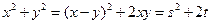, то
,
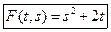то есть функция 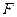найдена, а вместе с ней и частное решение исходного уравнения: 
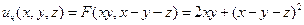. Мы построили частное решение в области 
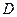. Но в данном случае легко убедиться, что найденное решение вместе со своими частными производными допускает непрерывное продолжение на ось 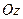, оставаясь при этом решением исходной задачи. Следовательно,
, 
.
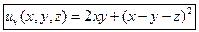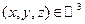Задание 1
Построить общее решение следующих уравнений.
1. 
;
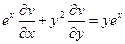2. 
;
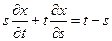3. 
;
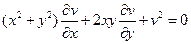4. 
;
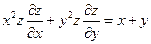5. 
;
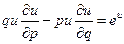6. 
;
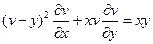7. 
;
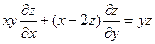8. 
;
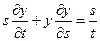9. 
;
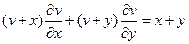10. 
;
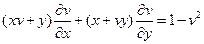11. 
;
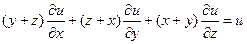12. 
;
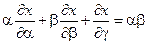13. 
;
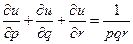14. 
;
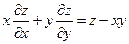15. 
;
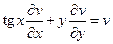16. 
;
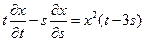17. 
;
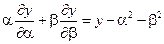18. 
;
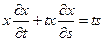19. 
;
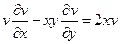20. 
;
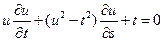21. 
;
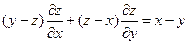22. 
;
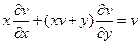23. 
;
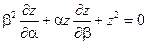24. 
;
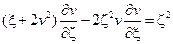25. 
.
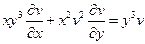Задание 2
Найти решения следующих уравнений, удовлетворяющие заданным граничным условиям:
1. 
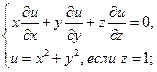
2. 
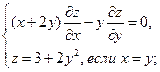
3. 
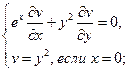
4. 
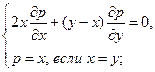
5. 
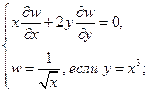
6. 
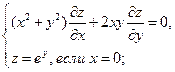
7. 
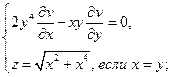
8. 
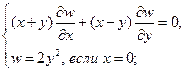
9. 
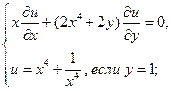
10. 
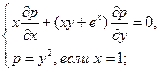
11. 
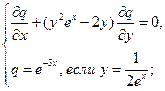
12. 
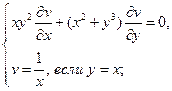
13. 
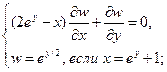
14. 
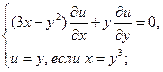
15. 
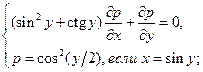
16. 
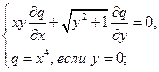
17. 
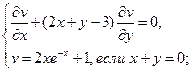
18. 
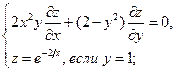
19. 
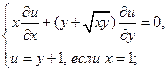
20. 
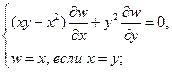
21. 
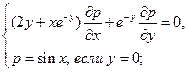
22. 
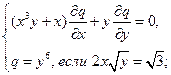
23. 
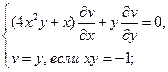
24. 
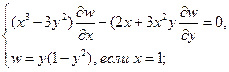
25. 
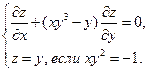
Задание 3.
В указанных областях для данных уравнений:
а) определить тип и привести уравнение к каноническому виду;
b) найти общее решение;
c) найти частное решение, удовлетворяющее заданным условиям.
1. 
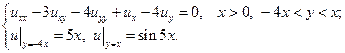
2. 
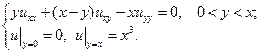
3. 
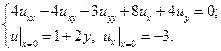
4. 
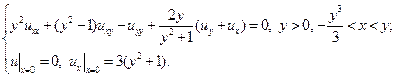
5. 
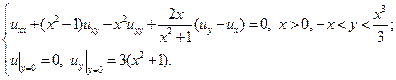
6. 
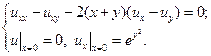
7. 
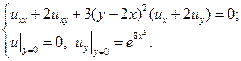
8. 
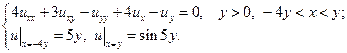
9. 
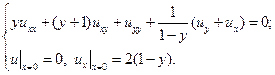
10. 
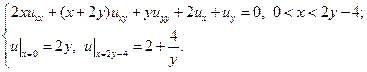
11. 
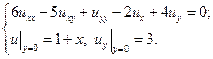
12. 
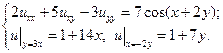
13. 
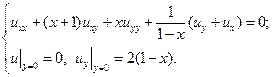
14. 
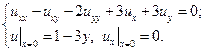
15. 
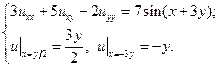
16. 
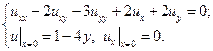
17. 
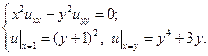
18. 
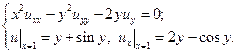
19. 
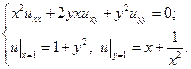
20. 
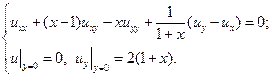
21. 
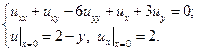
22. 
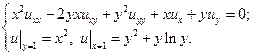
23. 
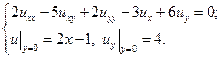
24. 
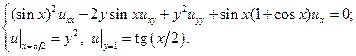
25. 
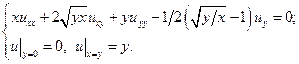
26. 
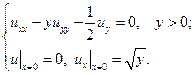
Пример 3.
Найти уравнение движения вынужденных колебаний полубесконечной струны со свободным левым концом, если в начальный момент времени струна имеет профиль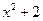 
, начальные скорости всех точек струны равны 
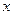, а плотность внешних сил (рассчитанных на единицу массы), которые действуют на струну, равна 
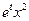. Натяжение струны равно ее линейной плотности.
Решение.
Уравнение движения струны в условиях задачи имеет вид:
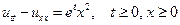. (4.1)
Это уравнение следует дополнить начальными условиями
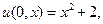
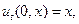(4.2)
и граничным условием на левом конце:
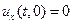. (4.3)
Таким образом, мы получили неоднородное волновое уравнение, для решения которого можно использовать либо интегральную формулу представления решения, либо метод подбора по правой части. В данном случае правая часть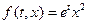 
имеет простой вид и позволяет сразу предположить вид частного решения уравнения (4.1): 
.
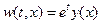Подставляя функцию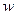 
в уравнение (4.1), получаем для 
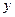уравнение 
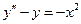, частное решение которого легко находится: 
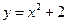. Следовательно, 
.
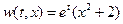Сделаем в уравнении (4.1), начальных условиях (4.2) и граничном условии (4.3) замену переменных
.
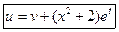Для функции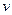 
получим следующую задачу:
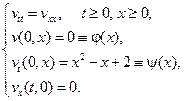
Учитывая вид граничного условия, продолжим функци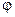и 
и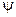 
на отрицательную ось четным образом: 
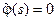при всех 
, 
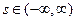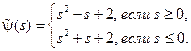
Применяя формулу Д' Аламбера, находим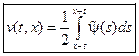 
.
При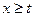 
получаем:
.
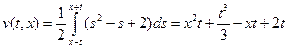При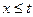 
, с учетом продолжения 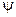, имеем: 
.
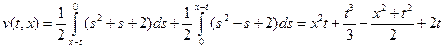Возвращаясь к функции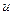 
, получаем решение исходной задачи:
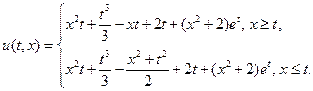
Задание 4.
Найти решения волновых уравнений, описывающих свободные колебания бесконечной или полубесконечной струны.
1. 
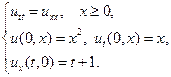
2. 
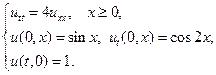
3. 
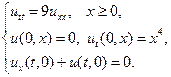
4. 
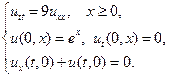
5. 
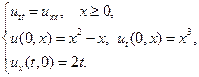
6. 
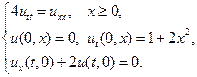
7. 
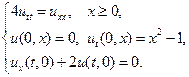
8. 
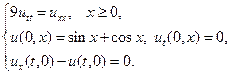
9. 
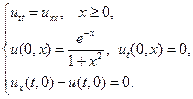
10. 
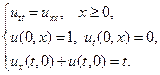
11. 
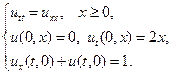
12. 
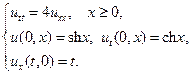
13. 
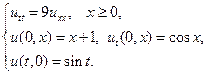
14. 
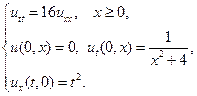
15. 
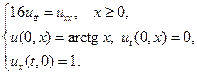
16. 
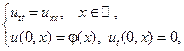
где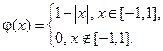 
Построить профиль струны в момент времени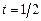 
.
17.
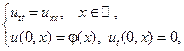
где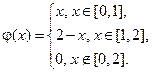 
Построить профиль струны в момент времени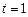 
.
18. 
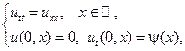
где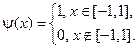 
Построить профиль струны в момент времени .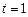
19.
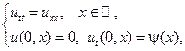
где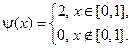 
Построить профиль струны в момент времени .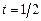
20.
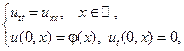
где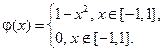 
Построить профиль струны в момент времени .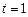
21. 
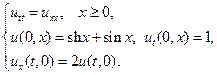
22. 
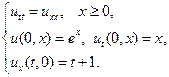
23.
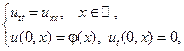
где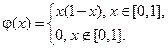 
Построить профиль струны в момент времени .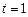
24. 
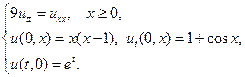
25.
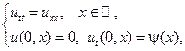
где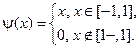 
Построить профиль струны в момент времени .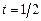
Задание 5.
Найти решения волновых уравнений, описывающих вынужденные колебания полубесконечной струны с заданными начальными условиями и граничным условием на левом конце.
1. 
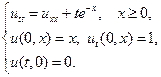
2. 
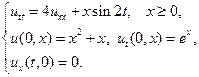
3. 
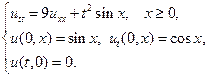
4. 
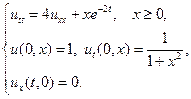
5. 
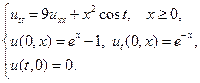
6. 
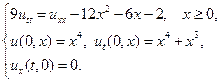
7. 
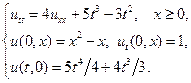
8. 
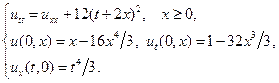
9. 
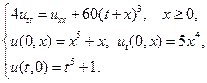
10. 
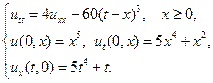
11. 
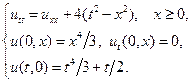
12. 
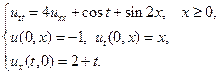
13. 
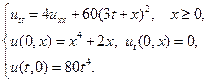
14. 
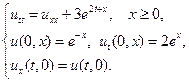
15. 
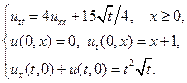
16. 
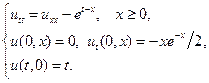
17. 
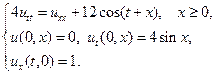
18. 
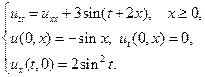
19. 
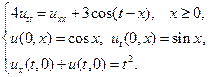
20. 
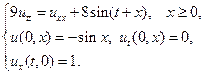
21. 
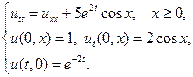
22. 
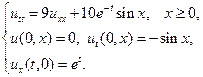
23. 
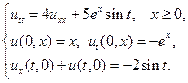
24. 
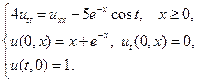
25. 
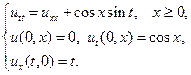
Пример 4.
Найти закон распространения тепла в тонком однородном стержне длины π, имеющем коэффициент температуропроводности равный 2, если начальная температура всех точек стержня равна нулю, его левый конец поддерживается при постоянной температуре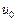 
, а правый конец и боковая поверхность теплоизолированы. Теплообмен несвободный: внутри стержня имеются источники и поглотители тепла, их интенсивность (в расчете на единицу массы стержня) равна 
.
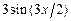Решение. Пусть стержень расположен вдоль отрезка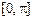 
, 
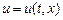– температура точки с координатой 
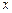в момент времени 
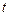. Уравнение теплопроводности в условиях задачи имеет вид
.
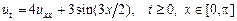Дополним уравнение начальным
,
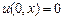и граничными условиями
, 
.
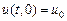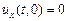Заменой переменных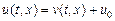 
преобразуем задачу к виду:
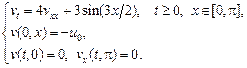(5.1)
Запишем соответствующую (5.1) задачу Штурма–Лиувилля:
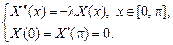(5.2)
Используя свойства собственных функций задачи Штурма–Лиувилля, заключаем, что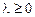 
. Легко видеть, что 
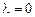не является собственным числом, т.к. в этом случае задача (5.2) имеет только тривиальные решения. Пусть 
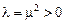, тогда общее решение уравнения (5.2) имеет вид 
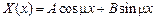. Из первого граничного условия находим, что 
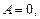из второго – что задача имеет нетривиальные решения только при 
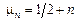, где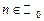 
. Следовательно, множество собственных чисел задачи (5.2) задается формулой 
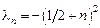, а соответствующие им собственные функции суть 
.
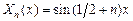Представим функцию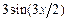 
в виде ряда, образованного ортогональной на 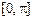системой 
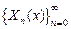. Из разложения
,
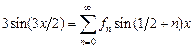в силу теоремы Стеклова, получаем, что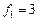 
, 
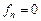при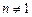 
.
Будем искать решение задачи (5.1) в виде ряда
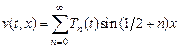, (5.3)
где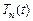 
– неизвестные, подлежащие определению функции. Заметим, что в силу (5.2) граничные условия для 
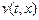выполняются автоматически. Подставим (5.3) в уравнение (5.1) и перенесем все слагаемые в левую часть:
.
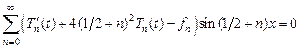Вновь применяя теорему Стеклова, получаем, что функции 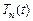должны удовлетворять уравнениям:
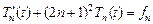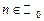, . (5.4)
Постоянные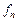 
были определены выше, и для нахождения 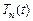нужно рассмотреть два случая.
· Если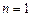 
, то уравнение (5.4) имеет вид 
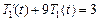, откуда следует, что 
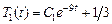, где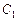 
– любое число.
· Если 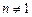, то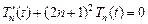 
, следовательно, 
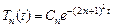, где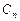 
– тоже произвольные числа.
Возвращаясь к представлению (5.3), получаем:
.
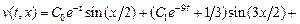
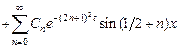Осталось найти постоянные 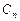. Для этого используем начальное условие:
.
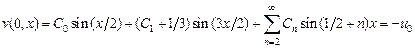Еще раз применяем теорему Стеклова и находим :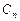
, 
,
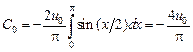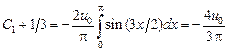и далее, при всех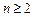 
, 
.
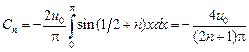Следовательно,
.
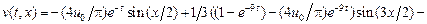
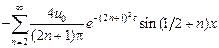Возвращаясь к функции 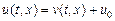, получаем решение исходной задачи:
.
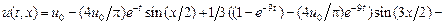
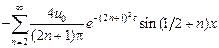Задание 6.
Применяя метод Фурье, найти решение следующих волновых уравнений на конечном отрезке.
1. 
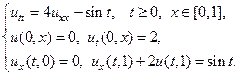
2. 
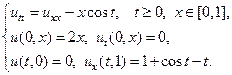
3. 
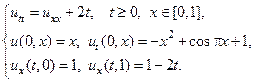
4. 
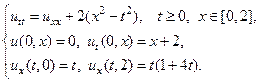
5. 
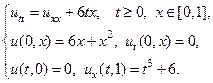
6. 
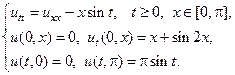
7. 
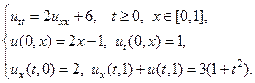
8. 
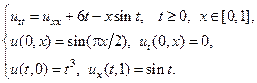
9. 
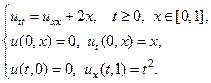
10. 
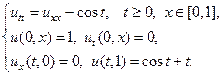
11. 
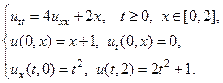
12. 
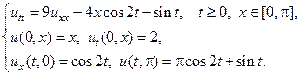
13. 
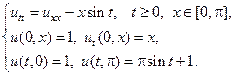
14. 
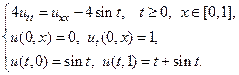
15. 
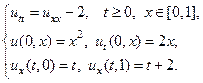
16. 
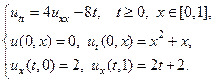
17. 
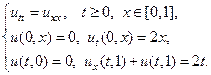
18. 
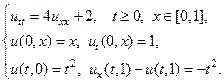
19. 
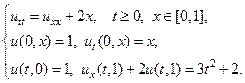
20. 
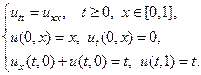
21. 
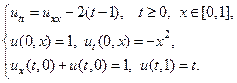
22. 
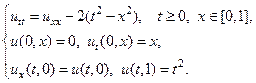
23. 
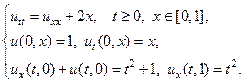
24. 
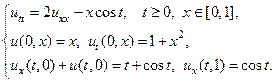
25. 
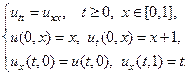
Задание 7.
Применяя метод Фурье, найти решение следующих уравнений теплопроводности на конечном отрезке.
1. 
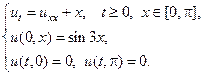
2. 
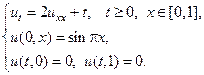
3. 
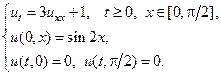
4. 
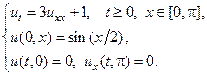
5. 
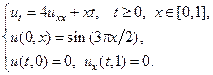
6. 
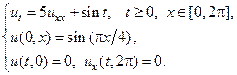
7. 
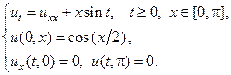
8. 
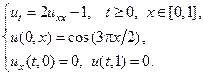
9. 
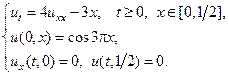
10. 
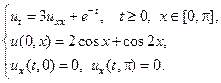
11. 
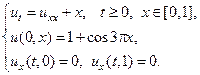
12. 
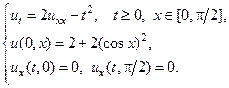
13. 
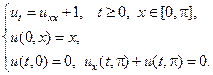
14. 
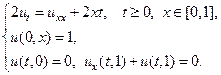
15. 
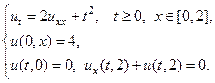
16. 
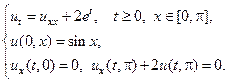
17. 
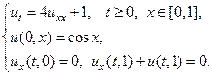
18. 
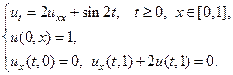
19. 
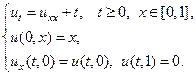
20. 
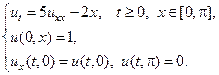
21. 
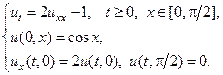
22. 
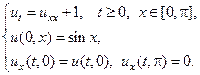
23. 
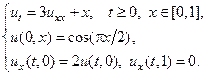
24. 
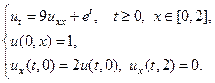
25. 
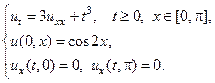
Пример 5.
Найти решение следующего уравнения теплопроводности с заданным начальным условием:
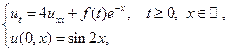
где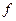 
– непрерывная при 
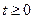функция.
Решение.
Решение данной задачи представимо в виде двух интегралов, один из которых учитывает начальное условие, а второй – влияние внутренних источников. Следовательно,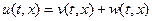 
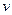, где и 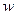находим по формулам Пуассона.
Для функции 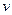справедливо следующее интегральное представление:
.
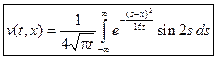Сделаем в интеграле замену переменных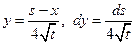 
:
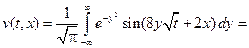
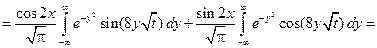
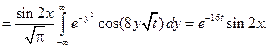
Применяем формулу для функции :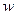
.
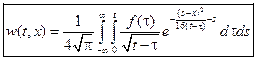Преобразуем показатель экспоненты, выделив полный квадрат по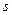 
:
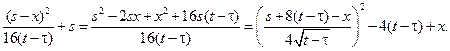Меняем порядок интегрирования, делаем замену переменных 
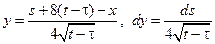и в итоге получаем:
.
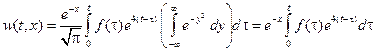Следовательно,
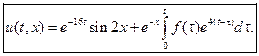
Задание 8.
Применяя формулы Пуассона, найти решения следующих уравнений теплопроводности для бесконечного стержня.
1. 
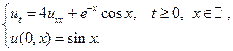
2. 
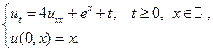
3. 
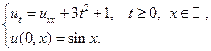
4. 
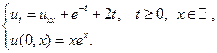
5. 
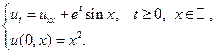
6. 
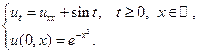
7. 
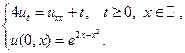
8. 
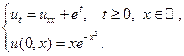
9. 
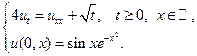
10. 
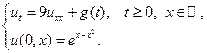
11. 
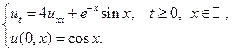
12. 
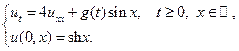
13. 
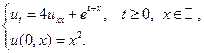
14. 
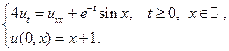
15. 
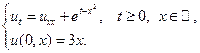
16. 
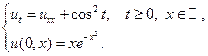
17. 
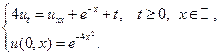
18. 
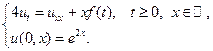
19. 
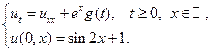
20. 
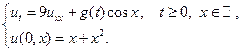
21. 
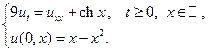
22. 
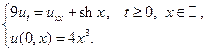
23. 
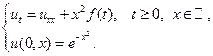
24. 
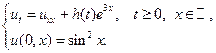
25. 
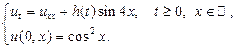
Пример 6.
Найти гармоническую в кольце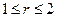 
функцию, удовлетворяющую краевым условиям: 
.
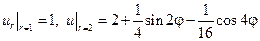Решение.
Пусть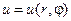 
– искомая функция. В силу определения гармонической функции, она является решением уравнения Лапласа с смешанными краевыми условиями на границах кольца:
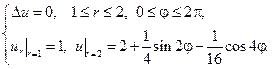
Используем представление решения уравнения Лапласа для кольца:
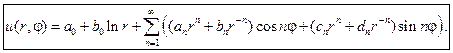Постоянные 
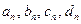найдем из граничных условий. Так как
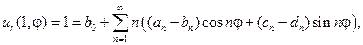
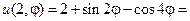
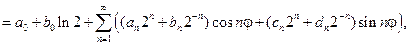
то, по формулам коэффициентов ряда Фурье, получаем:
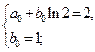
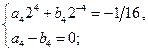
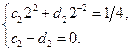
Все три системы однозначно разрешимы, из них находим: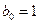 
, 
, 
, 
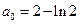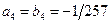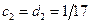. Далее, при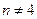 
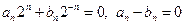, следовательно, 
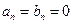; при 
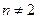
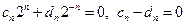, следовательно, 
.
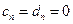Подставляя найденные коэффициенты в формулу представления решения, имеем окончательно:
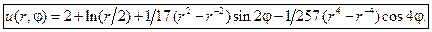
Задание 9.
Найти решения следующих краевых задач для уравнений Лапласа и Пуассона в заданных областях.
1. 
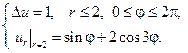
2. 
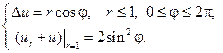
3. 
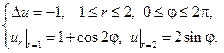
4. 
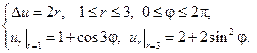
5. 
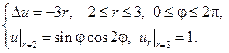
6. 
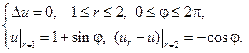
7. 
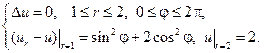
8. 
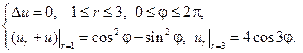
9. 
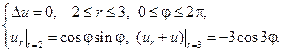
10. 
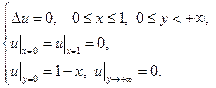
11. 
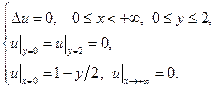
12. 
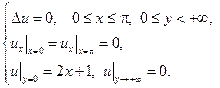
13. 
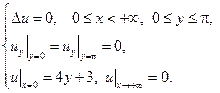
14. 
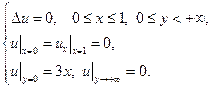
15. 
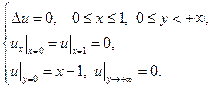
16. 
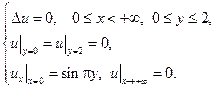
17. 
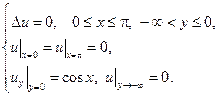
18. 
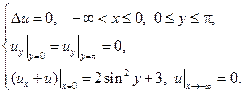
19. 
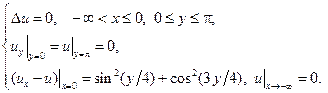
20. 
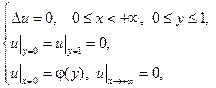
где 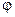– произвольная непрерывная функция.
21. 
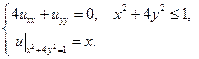
22. 
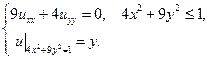
23. 
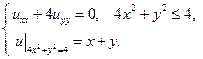
24. 
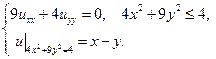
25. 
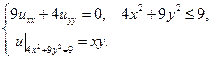
Пример 6.
Найти экстремаль функционала
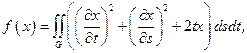(8.1)
где 
– единичный круг с центром в начале координат, с граничными условиями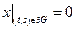 
.
Решение.
Как известно из курса вариационного исчисления, если функция 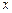– экстремаль функционала 
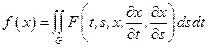, то она является решением уравнения Эйлера–Пуассона 
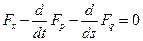, где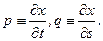 
Для функционала (8.1) 
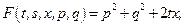следовательно,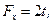 
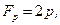
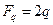, а уравнение Эйлера–Пуассона принимает вид:
,
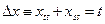то есть представляет собой уравнение эллиптического типа. Область, на которой ищется решение – внутренность круга (ограниченное множество), граница его – окружность, вдоль которой функция 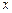обращается в нуль. Следовательно, искомая экстремаль является решением задачи Дирихле для внутренности круга.
Для круга естественно переформулировать задачу, перейдя к полярным координатам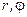 
. Пусть 
.
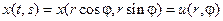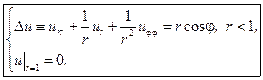(8.2)
Заменой переменных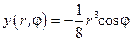 
сводим уравнение (8.2) к однородному (с ненулевыми граничными условиями):
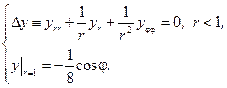(8.3)
Решение задачи (8.3) имеет представление в виде ряда:
.
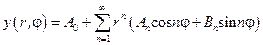Учитывая граничные условия, получаем:
,
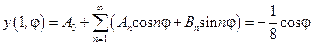откуда по формуле для коэффициентов ряда Фурье имеем:
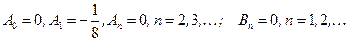. Следовательно, 
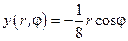, а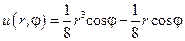 
. Возвращаясь к переменным 
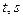и функции 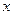, получаем решение уравнения Эйлера–Пуассона:
.
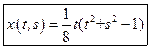Задание 10
Найти экстремали следующих функционалов в указанных областях с заданными условиями на границе.
1. 
,
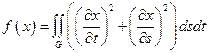– сектор круга: 
.
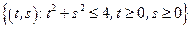Граничные условия: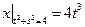 
, 
.
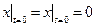2. 
,
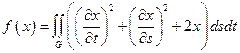– кольцо: 
.
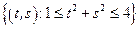Граничные условия: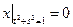 
, 
.
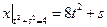3. 
,
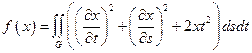– круг: 
.
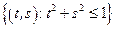Граничные условия: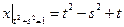 
.
4. ,
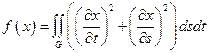– квадрат: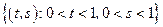 
.
Граничные условия: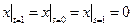 
, 
.
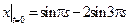5. ,
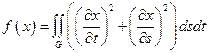– сектор кольца: 
.
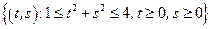Граничные условия: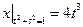 
, 
.
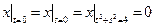6. ,
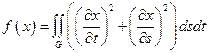– сектор круга: 
.
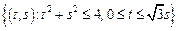Граничные условия: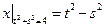 
, 
.
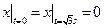7. 
,
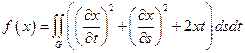– кольцо: 
.
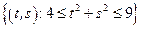Граничные условия: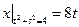 
, 
.
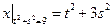8. 
,
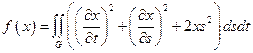– круг: 
.
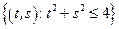Граничные условия: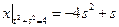 
.
9. ,
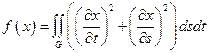– квадрат: .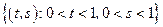
Граничные условия: