Прямая в пространстве. Взаимное расположение прямых

Канонические уравнения прямой в пространстве

Положение прямой в пространстве определено однозначно, если известна точка М₀(x₀; y₀; z₀), через которую она проходит, и ненулевой вектор 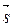= (т; п; р) параллельный этой прямой (рисунок 13). Вектор 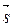называется направляющим вектором прямой.

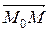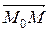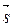Составим уравнение прямой по этим данным. Выберем произвольную точку М(x; y; z), принадлежащую прямой, и рассмотрим вектор = (х – х₀; у – у₀; z – z₀). Так как векторы и параллельны, то их одноименные координаты пропорциональны. Из условия коллинеарности векторов получим соотношения

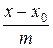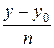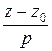= = , (4.1)

которым удовлетворяют координаты любой точки прямой.

Уравнения (4.1) называются каноническими уравнениями прямой.

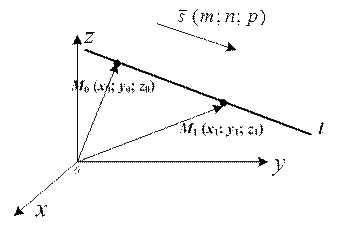
Рисунок 13 – Геометрическая иллюстрация к выводу уравнения (4.1)

Параметрические уравнения прямой в пространстве

В силу коллинеарности векторов 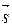= (т; п; р) и 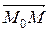существует t 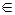R (t ≠0), такое, что 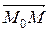= t 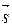или (х – х₀, у – у₀; z – z₀) = t(т, п; р). Тогда х – х₀ = tт, у – у₀ = tп, z – z₀ = tр, то есть

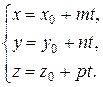(4.2)

Уравнения (4.2) называются параметрическими уравнениями прямой в пространстве.

Уравнение прямой в пространстве, проходящей через две данные точки

Уравнение прямой, проходящей через две данные точки М₁(х₁; у₁; z₁), М₂(х₂; у₂; z₂), рассмотрим как частный случай уравнения (4.1), когда направляющим вектором служит вектор 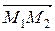. Получим

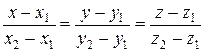. (4.3)

Уравнение (4.3) называется уравнением прямой, проходящей через две данные точки.

Общие уравнения прямой в пространстве

Прямую в пространстве можно однозначно определить как линию пересечения двух плоскостей, нормальные векторы которых 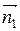= (А₁; В₁; С₁) и 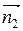= (А₂; В₂; С₂) непараллельны (рисунок 1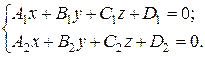4)

(4.4)

Уравнения (4.4) называются общими уравнениями прямой в пространстве.

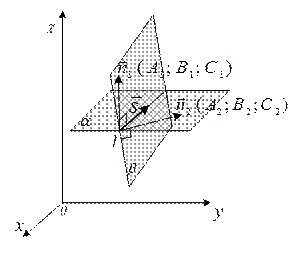
Рисунок 14 – Геометрическая иллюстрация к уравнению (4.4)

От общих уравнений прямой (4.4) можно перейти к каноническим уравнениям (4.1). Координаты некоторой точки М₀ можно найти, решив систему уравнений (4.4), придав одной из координат произвольное значение (например, z = 0).

Так как прямая перпендикулярна векторам 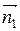= (А₁, В₁, С₁) и 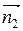= (А₂, В₂, С₂), то направляющий вектор 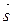также перпендикулярен этим векторам. Следовательно, в качестве направляющего вектора прямой можно взять вектор

= × = .

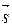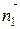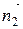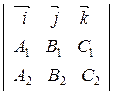Взаимное расположение двух прямых в пространстве

Угол между двумя прямыми

Углом между двумя прямыми в пространстве называют любой из двух углов, образованных прямыми, проведенными через произвольную точку пространства параллельно данным прямым.

Пусть заданы две прямые

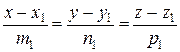и .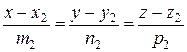

Один из двух углов между двумя прямыми, равен углу φ между их направляющими векторами 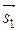= (т₁, п₁, р₁) и 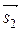= (т₂, п₂, р₂), а второй угол равен π – φ. Угол φ вычисляется по формуле

cosφ = .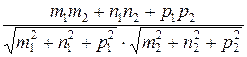

Условие перпендикулярности прямых

Прямые взаимно перпендикулярны тогда и только тогда, когда их направляющие векторы ортогональны. Отсюда следует, что их скалярное произведение равно нулю:

т₁т₂ + п₁п₂ + р₁р₂ = 0.