Двоичные функции двух аргументов
От двух двоичных аргументов x1 и x2 могут быть образованы шестнадцать разных двоичных функций yj=Fj(x1,x2), значения которых приведены в табл. 2. n = 2
Таблица 2
| x1 | x2 | y0 | y1 | y2 | y3 | y4 | y5 | y6 | y7 | y8 | y9 | y10 | y11 | y12 | y13 | y14 | y15 | |
| 22 | ||||||||||||||||||
N = 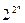 = 16 = 16 | ||||||||||||||||||
Если клетки в каждом столбце правой части табл. 2 рассматривать как разряды двоичного кода с весами от 20 (нижняя клетка) до 23 (верхняя клетка), то в столбцах оказываются записанными двоичные коды чисел, являющихся индексами у функций.
0. Функция y0 сохраняет нулевое значение при всех значениях аргументов. Она является константой нуля.
1. Функция y1 принимает единичное значение тогда и только тогда, когда оба аргумента принимают единичное значение. Такая функция называется конъюнкцией, а операция отыскания ее значения по заданным значениям аргументов называется операцией логического умножения или операцией И. Для обозначения операции логического умножения используется записи следующего вида:
y = x1 x2=x1&x2=x1·x2=x1x2
Произносится: y равно x1 И x2.
Конъюнкция может быть функцией любого конечного числа аргументов (n³2):
y = x1x2x3…xn.
Конъюнкция n аргументов принимает единичное значение тогда и только тогда, когда все n аргументов принимают единичное значение.
Операция логического умножения реализуется логическим элементом И, условное графическое обозначение которого приведено на Рис. 5, а..
2. Функция y2 принимает единичное значение тогда и только тогда, когда x1=1, а x2=0. Такая функция двух аргументов называется функцией запрета по x2 и реализуется с помощью логического элемента запрета, представляющего собой элемент И с одним инверсным входом (Рис. 5, б).
3. Функция y3 повторяет значения аргумента x1, является тавтологией x1 и реализуется повторителем ( Рис. 3, а).
4. Функция y4 является функцией запрета по x1 и реализуется с помощью элемента запрета (Рис. 5, в).
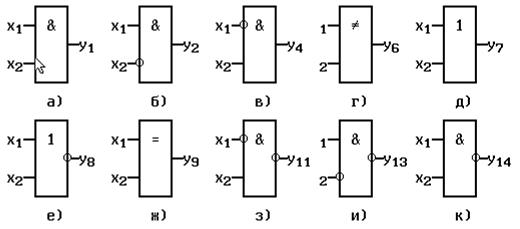
Рис. 5 Элементарные автоматы без памяти (двоичные функции двух аргументов)
5. Функция y5 повторяет значения аргумента x2, является тавтологией x2 и реализуется повторителем (Рис. 3, а).
6. Функция y6 принимает единичные значения тогда и только тогда, когда аргументы имеют разные значения (0 и 1 или 1 и 0). Такая функция называется функцией неравнозначности:
y = x1¹x2.
Функция реализуется логическим элементом неравнозначности, УГО которого приведено на Рис. 5, г.
Операция отрицания равнозначности может быть распространена на любое конечное число аргументов (n ³ 2):
y = x1 ¹ x2 ¹ … ¹ xn.
Функция неравнозначности принимает нулевое значение в том и только в том случае, если значения всех ее аргументов одинаковы (все равны 0 или все равны 1).
7. Функция y7 принимает единичное значение в том случае, если хотя бы один из ее аргументов принимает единичное значение. Такая функция называется дизъюнкцией, а соответствующая ей операция - операцией логического сложения или операцией ИЛИ. Обозначается:
y = x1Vx2.
Произносится: y равно x1 ИЛИ x2.
Дизъюнкция может быть функцией любого конечного числа аргументов (n ³2):
y = x1Vx2V…Vxn.
Дизъюнкция n аргументов принимает единичное значение, когда хотя бы один аргумент принимает единичное значение. Данная функция реализуется логическим элементом ИЛИ, условное графическое обозначение которого приведено на Рис. 5, д.
8. Функция y8 принимает единичное значение тогда и только тогда, когда оба аргумента принимают нулевое значение. Такая функция называется функцией Даггера или стрелкой Пирса, а соответствующая ей операция - операцией Пирса или операцией ИЛИ-НЕ. Обозначается:
y =x1¯x2 или y = 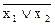 .
.
Операция ИЛИ-НЕ может быть распространена на любое конечное число аргументов (n ³ 2):
y = 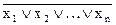 .
.
Функция Даггера принимает единичное значение тогда и только тогда, когда все ее аргументы равны нулю. Функция реализуется логическим элементом ИЛИ-НЕ (Рис. 5, е).
9. Функция y9 принимает единичное значение в том случае, если оба ее аргумента принимают одинаковые значения (00 или 11) Такая функция называется эквиваленцией, а соответствующая ей операция - операцией равнозначности. Обозначается:
y = x1 = x2.
Произносится: y равно x1 равнозначно x2.
Операция равнозначности может быть распространена на любое конечное число аргументов (n ³ 2):
y = x1 = x2 = ... = xn.
Функция эквиваленция принимает единичное значение только при нулевых значениях или только при единичных значениях всех ее аргументов. Функция реализуется логическим элементом равнозначности (Рис. 5, ж).
10. Функция y10 принимает значения, противоположные значениям аргумента x2, и является инверсией аргумента x2. Реализуется логическим элементом НЕ (Рис. 3, б).
11. Функция y11 принимает значение тогда и только тогда, когда аргументы x1 принимает нулевое значение, а аргумент x2 - единичное значение. Такая функция называется импликацией из x2, а соответствующая ей операция - операцией следования из x2. Обозначается:
y = x2 ® x1.
Функция реализуется логическим элементом - импликатором (Рис. 5, з).
12. Функция y12 принимает значения, противоположные значениям ее аргумента x1, и является инверсией аргумента x1 (y12= 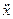 1.). Реализуется элементом НЕ (Рис. 3, б).
1.). Реализуется элементом НЕ (Рис. 3, б).
13. Функция y13 является импликацией из x1. Обозначается: y = x1®x2 и реализуется логически элементом, условное графическое обозначение которого приведено на Рис. 5, и.
14. Функция y14 принимает нулевое значение тогда и только тогда, когда оба ее аргумента принимают единичное значение. Такая функция называется функцией Шеффера или операцией И-НЕ. Обозначается:
y = x1/x2 или y = 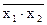 .
.
Операция может быть распространена на любое конечное число аргументов (n³2):
y = 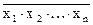 .
.
Функция Шеффера принимает нулевое значение тогда и только тогда, когда все ее аргументы принимают единичное значение. Реализуется данная функция логическим элементом И-НЕ (Рис. 5, к).
15. Функция y15 сохраняет единичное значение при всех наборах значений аргументов и является константой единицы.
