Определение равнодействующей

Аналитическим способом

Знать аналитический способ определения равнодействующей силы, условия равновесия плоской сходящейся системы сил в ана­литической форме.

Уметь определять проекции силы на две взаимно перпендику­лярные оси, решать задачи на равновесие в аналитической форме.

Проекция силы на ось

Проекция силы на ось определяется отрезком оси, отсекаемым перпендикулярами, опущенными на ось из начала и конца вектора (рис. 3.1).

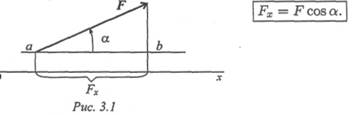
Величина проекции силы на ось равна произведению модуля си­лы на косинус угла между вектором силы и положительным напра­влением оси. Таким образом, проекция имеет знак: положительный при одинаковом направлении вектора силы и оси и отрицательный при направлении в сторону отрицательной полуоси (рис. 3.2).

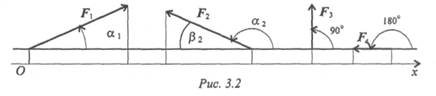
20 Лекция 3

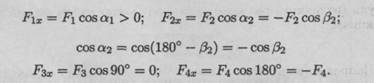
Проекция силы на две взаимно перпендикулярные оси (рис. 3.3).

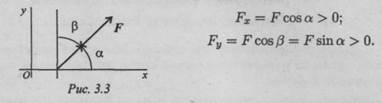
Определение равнодействующей системы сил аналитическим

Способом

Величина равнодействующей равна векторной (геометрической) сумме векторов системы сил. Определяем равнодействующую геоме­трическим способом. Выберем систему координат, определим про­екции всех заданных векторов на эти оси (рис. 3.4а). Складываем проекции всех векторов на оси х и у (рис. 3.46).

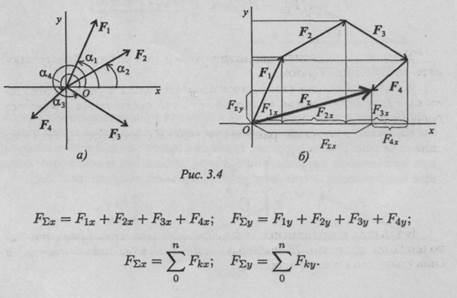
Тема 1.2. Плоская система сходящихся сил 21

Модуль (величину) равнодействующей можно найти по известным проекциям:

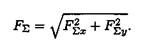
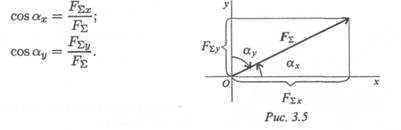
Направление вектора равнодействующей можно определить по величинам и знакам косинусов углов, образуемых равнодействующей с осями координат (рис. 3.5).

Условия равновесия плоской системы сходящихся сил в аналитической форме

Исходя из того, что равнодействующая равна нулю, получим:

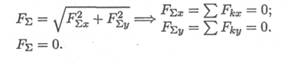
Условия равновесия в аналитической форме можно сформулиро­вать следующим образом:

Плоская система сходящихся сил находится в равновесии, ес­ли алгебраическая сумма проекций всех сил системы на любую ось равна нулю.

Система уравнений равновесия плоской сходящейся системы сил:

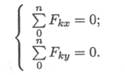
В задачах координатные оси выбирают так, чтобы решение бы­ло наиболее простым. Желательно, чтобы хотя бы одна неизвестная сила совпадала с осью координат.

22 Лекция 3

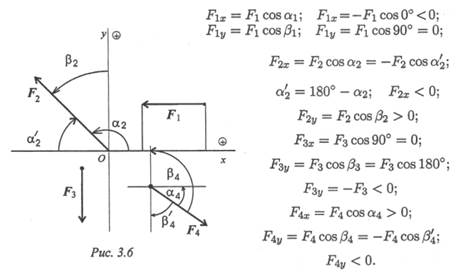
Пример 1.Определить величины и знаки проекций предста­вленных на рис. 3.6 сил.

Решение

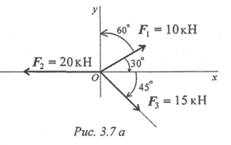
Пример 2.Определить величину и направление равнодейству­ющей плоской системы сходящихся сил аналитическим способом.

Решение

1. Определяем проекции всех сил системы на Ох (рис. 3.7а):

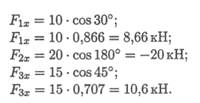
Сложив алгебраически проекции, получим проекцию равнодей­ствующей на ось Ох.

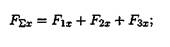
Тема 1.2. Плоская система сходящихся сил 23

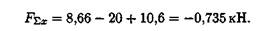
Знак говорит о том, что равнодействующая направлена влево.

2. Определяем проекции всех сил на ось Оу значения проекций, получим величину проекции Оу.

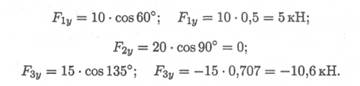
Сложив алгебраически значения проек­ций, получим величину проекции равнодей­ствующей на ось Оу.

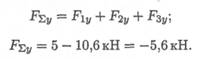
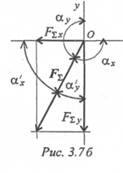
Знак проекции соответствует направле­нию вниз. Следовательно, равнодействую­щая направлена влево и вниз (рис. 3.76).

3. Определяем модуль равнодействующей по величинам проекций:

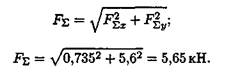
4. Определяем значение угла равнодействующей с осью Ох:

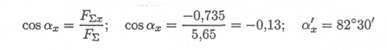
и значение угла с осью Оу:

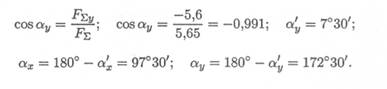
24 Лекция 3

Пример 3.Система трех сил находится в равновесии. Известны проекции двух сил системы на взаимно перпендикулярные оси Ох и Оу:

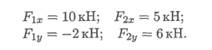
Определить, чему равна и как направлена третья сила системы.

Решение

1. Из уравнений равновесия системы определяем:

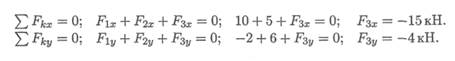
2. По полученным величинам проекций определяем модуль силы:

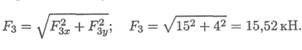
3. Направление вектора силы относительно оси Ох (рис. 3.8):

­

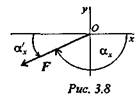
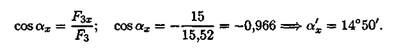
Угол с осью Ох будет равен

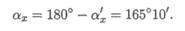
Контрольные вопросы и задания

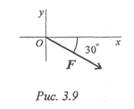
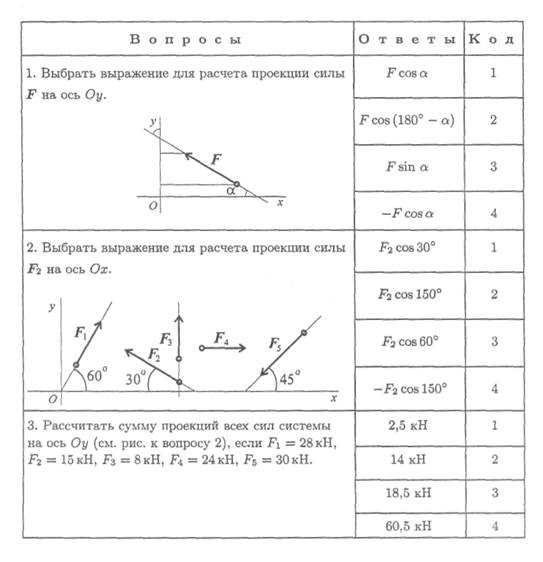
1. Запишите выражение для расчета проекции силы JF на ось Оу (рис. 3.9).

Тема 1.2. Плоская система сходящихся сил 25

2. Определите сумму проекций сил системы на ось Ох
(рис. 3.10).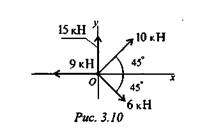

3. Определите величину силы по известным проекциям:

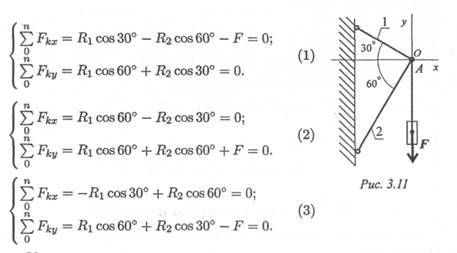
4. Груз находится в равновесии (рис. 3.11). Какая система урав-­
нений равновесия для шарнира А записана верно?

Указания.

1. При ответе на вопросы 1 и 2 необходимо знать, что в выраже­-
ние для величины проекции силы на ось подставляется угол между
вектором силы и положительной полуосью координат. Не забыть,
что определяется алгебраическая сумма.

2. При ответе на вопрос 4 сначала следует определить возмож-
ные направления реакций в стержнях, мысленно убирая по очереди

26 Лекция 3

стержни и рассматривая возможные перемещения (см. лекцию 1). Затем записать алгебраические суммы проекций сил на оси Ох и Оу. Полученные уравнения сравнить с приведенными. 5. Ответьте на вопросы тестового задания.

Тема 1.2. Статика.

Проекции силы на ось

Тема 1.2. Плоская система сходящихся сил 27

130 Практическое занятие 1