Стационарные временные ряды и их характеристики. Автокорреляционная функция

Важное значение в анализе временных рядов имеют стационарные временные ряды, вероятностные свойства которых не изменяются во времени.

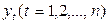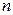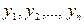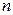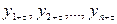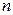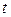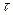Временной ряд называется стационарным, если совместное распределение вероятностей наблюдений такое же, как и наблюдений при любых , и . Другими словами, свойства строго стационарных рядов 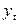не зависят от момента 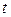, т.е. закон распределения и его числовые характеристики не зависят от 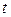. Следовательно, математическое ожидание 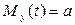, среднее квадратическое отклонение 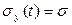могут быть оценены по наблюдениям с помощью формул:

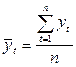(7.4)

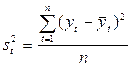(7.5)

Простейшим примером стационарного временного ряда, у которого математическое ожидание равно нулю, а ошибки 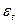некоррелированы, является «белый шум».

Степень тесноты связи между последовательностями наблюдений временного ряда 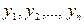и 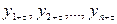(сдвинутых относительно друг друга на 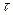единиц, или, как говорят, с лагом 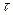) может быть определена с помощью коэффициента корреляции

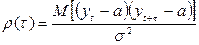(7.6)

Т.к. 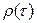измеряет корреляцию между членами одного и того же ряда, его называют коэффициентом автокорреляции, а зависимость 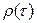– автокорреляционной функцией. В силу стационарности временного ряда 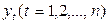автокорреляционная функция 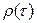зависит только от лага 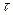, причем 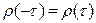, т.е. при изучении можно ограничиться рассмотрением только положительных значений .

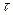Статистической оценкой 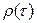является выборочный коэффициент автокорреляции 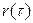, определяемый по формуле:

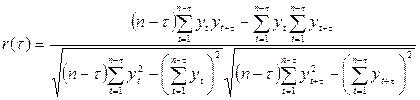(7.7)

Функцию 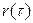называют выборочной автокорреляционной функцией, а ее график – коррелограммой.

При расчете 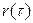следует помнить, что с увеличением 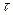число 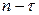пар наблюдений 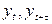уменьшается, поэтому лаг 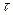должен быть таким, чтобы число 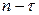было достаточным для определения 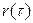. Обычно ориентируются на соотношение .

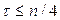Для стационарного временного ряда с увеличением лага 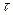взаимосвязь членов временного ряда 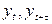ослабевает, и автокорреляционная функция 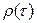должна убывать (по абсолютной величине). В то же время для ее выборочного (эмпирического) аналога 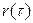, особенно при небольшом числе пар наблюдений 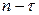, свойство монотонного убывания (по абсолютной величине) при возрастании 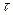может нарушаться.

Наряду с автокорреляционной функцией при исследовании стационарных рядов рассматривается частная автокорреляционная функция 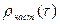, где 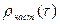есть частный коэффициент корреляции между членами временного ряда 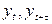, т.е. коэффициент корреляции между 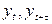и при устранении влияния промежуточных между 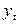и 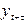членов.

Статистической оценкой 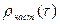является выборочная частная автокорреляционная функция 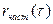, где 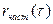– выборочный частный коэффициент корреляции, определяемый по формуле (7.6) или (7.7). Например, выборочный частный коэффициент автокорреляции 1-го порядка между членами временного ряда 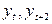при устранении влияния 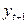может быть вычислен по формуле:

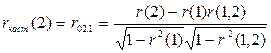(7.8)

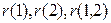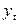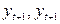где – выборочные коэффициенты автокорреляции между и 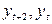и и .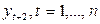

Пример 2

Таблица 2

Год,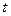
Спрос,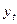

Приведены данные, отражающие спрос на некоторый товар за восьмилетний период (усл. ед.), т.е. временной ряд спроса .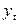

По данным таблицы 2 для временного ряда найти среднее значение, среднее квадратическое отклонение, коэффициенты автокорреляции (для лагов 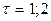) и частный коэффициент автокорреляции 1-го порядка.

Решение.

Среднее значение временного ряда находим по формуле:

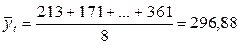(ед.).

Дисперсию и среднее квадратическое отклонение можно вычислить по формуле, но в данном случае проще использовать соотношение

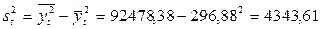
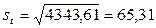(ед.)

где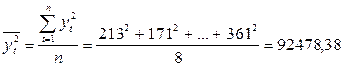

Найдем коэффициент автокорреляции 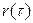временного ряда (для лага 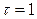), т.е. коэффициент корреляции между последовательностями семи пар наблюдени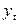й и :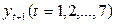

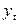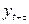Вычисляем необходимые суммы:

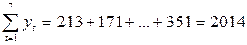
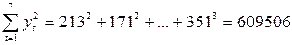
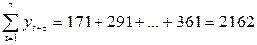
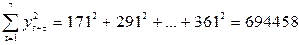
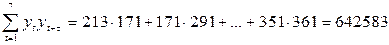
Теперь по формуле (7.7) коэффициент автокорреляции

.

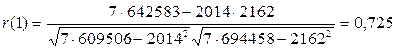Коэффициент автокорреляции 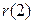для лага 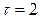между членами ряда 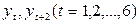по шести парам наблюдений вычисляем аналогично: .

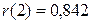Для определения частного коэффициента корреляции 1-го порядка 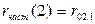между членами ряда 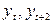при исключении влияния 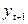вначале найдем (по аналогии с предыдущим) коэффициент автокорреляции 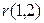между членами ряда: 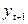и 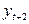: 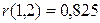, а затем вычислим 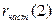по формуле (7.8):

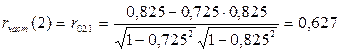
Знание автокорреляционных функций оказывает существенную помощь при подборе и идентификации модели анализируемого временного ряда и статистической оценке его параметров.