Эконометрического моделирования

ТЕМА 1.1. ОСНОВНЫЕ АСПЕКТЫ

ЭКОНОМЕТРИЧЕСКОГО МОДЕЛИРОВАНИЯ

План лекции

1. Предмет, цель и задачи эконометрики.

2. Этапы становления эконометрики.

3. Введение в эконометрическое моделирование.

4. Основные математические предпосылки эконометрического моделирования.

5. Основные этапы и проблемы эконометрического моделирования.

Введение

Переход к рыночной экономике повышает требования к качеству подготовки экономистов, которые должны владеть количественными методами анализа в экономике и должны быть востребованы на рынке труда. Деятельность экономиста должна содержать прогностическую составляющую, обеспечивающую возможность заранее сигнализировать о наступлении тех или иных «особых» ситуаций. Если в период централизованной плановой экономики упор делался на балансовых и оптимизационных методах исследования, то в период рыночной экономики возрастает роль эконометрических методов.

Предмет, цель и задачи эконометрики.

Дисциплина «Эконометрика» относится к федеральному компоненту цикла общих математических и естественнонаучных дисциплин.

Термин «эконометрика» (экономика и метрика) был введен норвежским ученым Рагнаром Фришем (1895 – 1973 г.) в 1926 г. для обозначения нового направления в экономической науке, предназначенного для количественного анализа экономических процессов и явлений.

Эконометрика является одним из разделов математического моделирования экономических процессов, который базируется:

1) на экономической теории;

2) теории вероятностей и математической статистике;

3) экономической статистике и экономических измерениях.

Определение 1:

Эконометрика – это научная дисциплина, объединяющая совокупность теоретических результатов, методов и приемов экономической теории, экономической статистики и математико-статистического инструментария для количественного выражения качественных закономерностей в экономике.

Зарождение эконометрики является следствием междисциплинарного подхода к изучению экономики. Эта наука возникла в результате взаимодействия и объединения в особый «сплав» трех компонент: экономической теории, статистических и математических методов.

Этапы становления эконометрики

1930 г. Образовано эконометрическое общество, основатели которого – И.Фишер, Р.Фриш, О.Андерсон, Я. Тинберген и др.

1933 г. Начал издаваться журнал «Econometrica», который и сейчас играет важную роль в развитии эконометрической науки.

1930-1939г. Я.Тинберген начал макроэконометрическое моделирование.

1941 г. Появился первый учебник по эконометрике, написанный Я.Тинбергеном.

1955 г. Л.Клейном и А.Гольдбергом была построена одна из первых комплексных эконометрических моделей, которая состояла из 15 регрессионных уравнений и охватывала 40 макроэкономических показателей по данным за 20 лет.

В нашей стране первая попытка внедрить эконометрику в советскую школу принадлежит В.С.Немчинову (1960 г.). Эта попытка привела к выделению направлений «экономико-математические методы» и «экономическая кибернетика». И только с 1995 г. эконометрика стала по-настоящему развиваться в России. С 2006 г. в нашей стране выходит ежеквартальный журнал «Прикладная эконометрика».

Последние десятилетия эконометрика как научная дисциплина стремительно развивается. Свидетельством всемирного признания эконометрики является присуждение за разработки в этой области Нобелевских премий по экономике Р. Фришу и Я. Тинбергу (1969 г.)., Л. Клейну (1980 г.), Т. Хаавельмо (1989 г.), Дж. Хекману и Д. Макфаддену (2000г.).

Основные математические предпосылки

Основные этапы и проблемы

Эконометрического моделирования

Можно выделить 6 этапов эконометрического моделирования: постановочный, априорный, этап параметризации, информационный, этапы идентификации и верификации.

Этап – постановочный.

Формируется цель исследования, набор участвующих в модели экономических переменных. При выборе экономических переменных необходимо теоретическое обоснование каждой переменной. Объясняющие переменные не должны быть связаны функциональной или тесной корреляционной зависимостью.

Этап – априорный.

Проводится анализ сущности изучаемого объекта, формирование и формализация априорной (известной до начала моделирования) информации.

Этап – параметризация.

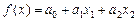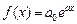Осуществляется непосредственно моделирование, выбор общего вида модели, т.е. выбор функции или . На этом этапе происходит выражение в математической форме обнаруженных связей и соотношений, установление экзогенных (независимых) и эндогенных (зависимых) переменных.

Этап – информационный.

Осуществляется сбор необходимой статистической информации – наблюдаемых значений экономических переменных.

Этап – верификация модели.

Проводится проверка адекватности модели, делается вывод о том, какова точность расчетов на основе модели, т.е. проводится анализ остатков.

Принято различать следующие три группы моделей эконометрики:

· регрессионная модель – это уравнение, в котором объясняемая переменная выступает в виде функции от объясняющих переменных. В таких моделях зависимая (объясняемая) переменная y представляется в виде функции 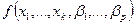, где 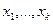– независимые (объясняющие) переменные, а 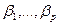– некоторые параметры. В зависимости от вида функции 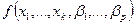модели делятся на линейные и нелинейные.

· системы одновременных уравнений состоят из набора регрессионных уравнений и некоторых тождеств. Данные модели описываются системами уравнений. Системы могут состоять из тождеств и регрессионных уравнений, в которые могут входить не только объясняющие, но и объясняемые переменные.

· модели временных рядов включают процедуры анализа, синтеза, а также прогноза. Модели временных рядов предполагают выделение в них таких компонент, как тренд (основная тенденция) 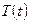, периодическая (осциллятивная, конъюнктурная, сезонная) компонента 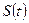, а также случайная (стохастическая) компонента 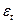. Модели временных рядов принято делить на аддитивные, мультипликативные и смешанные:

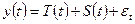(аддитивная модель),

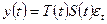(мультипликативная модель),

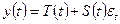(смешанная модель).

Эконометрическое оценивание моделей включает два основных этапа:

· теоретический. Предпосылкой теоретического этапа выступает следующее представление. Считается, что определено все множество реализаций экономических показателей, или, на языке выборочного метода статистики, определена генеральная совокупность. Зная или полагая те или иные статистические свойства генеральной совокупности, можно теоретически определить параметры модели;

· эмпирический. На эмпирическом этапе исследователь располагает лишь выборочными значениями экономических показателей. На этом этапе можно оценить, но нельзя точно определить значения параметров модели, поскольку они являются случайными величинами. Оценка проводится, чтобы получить как можно более точные и статистически достоверные значения неизвестных параметров модели, которые характеризуют генеральную совокупность всех возможных реализаций экономических показателей.

Характеристики генеральной совокупности, как правило, неизвестны, поэтому их оценивают по выборочным данным. Согласно выборочному методу статистики характеристики генеральной совокупности принято называть параметрами, а характеристики выборочной совокупности – оценками. Выборочная оценка дает удовлетворительное приближение для оцениваемого параметра, если она отвечает ряду требований. Эти требования характеризуются такими терминами, как «несмещенность», «эффективность» и «состоятельность». Напомним их определения.

Оценка называется несмещенной, если ее математическое ожидание равно оцениваемому параметру при любом объеме выборки. В противном случае оценка называется смещенной.

Несмещенная оценка называется эффективной, если она имеет минимальную дисперсию по сравнению с другими выборочными оценками.

Оценка называется состоятельной, если при увеличении объема выборки она стремится по вероятности к оцениваемому параметру.

Контрольные вопросы:

1. Дайте определение эконометрики.

2. С какими науками связана эконометрика?

3. Когда возникло эконометрическое общество и журнал «Эконометрика»?

4. Каковы этапы эконометрического моделирования?

5. Какие группы моделей принято различать в эконометрике?

6. Что такое экзогенные и эндогенные переменные?

7. Каким свойствам должны удовлетворять оценки параметров?

И КОРРЕЛЯЦИЯ

План лекции

1. Модель линейной парной регрессии. Метод наименьших квадратов.

2. Коэффициент корреляции.

3. Основные положения регрессионного анализа. Теорема Гаусса – Маркова.

4. Оценка значимости уравнения регрессии. Коэффициент детерминации.

5. Построение интервальных прогнозов по модели парной регрессии.

Введение

В экономике в большинстве случаев между переменными величинами существуют зависимости, когда каждому значению одной переменной соответствует множество возможных значений другой переменной. Иначе говоря, каждому значению одной переменной соответствует определенное (условное) распределение другой переменной. Такая зависимость получила название статистической.

В силу неоднозначности статистической зависимости между 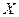и 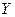для исследователя, в частности, представляет интерес усредненная по 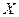схема зависимости. Если зависимость между двумя переменными такова, что каждому значению одной переменной соответствует определенное условное математическое ожидание (среднее значение) другой, то такая статистическая зависимость называется корреляционной. Корреляционная зависимость может быть представлена в виде

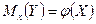или .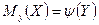

В регрессионном анализе рассматриваются односторонняя зависимость случайной переменной 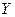от одной (или нескольких) неслучайной независимой переменной 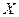. Такая зависимость может возникнуть, например, в случае, когда при каждом фиксированном значении 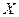соответствующие значения 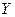подвержены случайному разбросу за счет действия ряда неконтролируемых факторов.

Зависимость такого типа, выражаемая соотношением

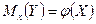(2.1)

называется функцией регрессии 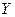на 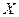. При этом 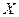называется независимой (объясняющей) переменной (регрессором), 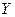– зависимой (объясняемой) переменной. При рассмотрении зависимости двух случайных величин говорят о парной регрессии.

В статистической практике исследователь располагает лишь выборкой пар значений 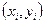ограниченного объема п. В этом случае речь может идти об оценке (о приближенном выражении) по выборке функции регрессии. Такой оценкой является выборочное уравнение регрессии:

,

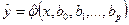где 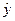– условная (групповая) средняя переменной 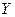при фиксированном значении переменной 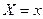; 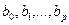– параметры регрессии.

При правильно определенной аппроксимирующей функции 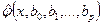с увеличением объема выборки 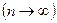она будет сходиться по вероятности к функции регрессии .

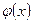Метод наименьших квадратов

Если функция регрессии линейна, то говорят, о линейной регрессии.

Линейная регрессия находит широкое применение в эконометрике ввиду четкой экономической интерпретации ее параметров.

Линейная регрессия сводится к нахождению уравнения вида

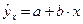или 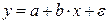. (2.2)

Уравнение вида 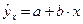позволяет по заданным значениям фактора иметь теоретические знания результативного признака подстановкой в него фактических значений фактора .

Построение линейной регрессии сводится к оценке ее параметров – и . Оценки параметров линейной регрессии могут быть найдены разными методами.

Классический подход к оцениванию параметров линейной регрессии основан на методе наименьших квадратов (МНК).

Метод наименьших квадратов позволяет получить такие оценки параметров и , при которых сумма квадратов отклонений фактических значений результативного признака 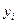от расчетных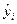 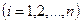минимальна:

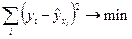(2.3)

Иными словами, из всего множества линий линия регрессии на графике выбирается так, чтобы сумма квадратов расстояний по вертикали между точками и этой линией была бы минимальной:

,

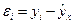следовательно,

.

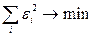Для того чтобы найти минимум функции (2.3), надо вычислить частные производные по каждому из параметров и и приравнять их к нулю.

Обозначим 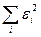через 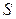, тогда:

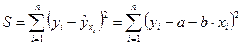
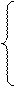
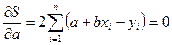
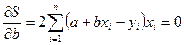(2.4)

Преобразуя формулу (2.4), получим следующую систему нормальных уравнений для оценки параметров и :

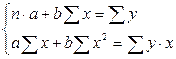(2.5)

Теперь, разделив обе части уравнений (2.5) на 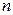, получим систему нормальных уравнений в виде:

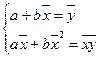, (2.6)

где соответствующие средние определяются по формулам:

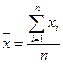, (2.7)

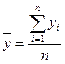, (2.8)

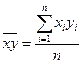, (2.9)

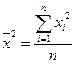. (2.10)

Подставляя значение

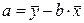(2.11)

из первого уравнения системы (2.6) в уравнение регрессии 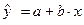, получим

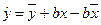
или

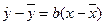. (2.12)

Решая систему нормальных уравнений (2.5) либо методом последовательного исключения переменных, либо по формулам Крамера, найдем искомые оценки параметров и .

Поскольку ковариация 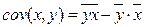, а дисперсия признака Х 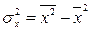, получим следующую формулу расчета оценки параметра :

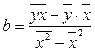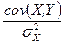= (2.13)

Параметр называется коэффициентом регрессии. Его величина показывает среднее изменение результата с изменением фактора на одну единицу. Так, если функция издержек (У, тыс. руб.) выражается как 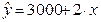, ( – количество единиц продукции), то, следовательно, с увеличением объема продукции на одну единицу издержки производства возрастают в среднем на 2 тыс. руб., т.е. дополнительный прирост продукции на одну единицу потребует увеличения затрат в среднем на 2 тыс. руб.

Знак при коэффициенте регрессии показывает направление связи: при 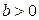– связь прямая, а при 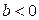– связь обратная.

Параметр может не иметь экономического содержания.

Пример 1.

По группе предприятий выпускающих один и тот же вид продукции, рассматривается функция издержек 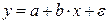. Необходимая для расчета оценок параметров и информация представлена в таблице.

Расчетная таблица
Номер предприятия	Выпуск продукции, тыс. ед.	Затраты на производство, млн. руб.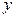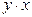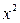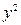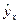
						31,1
						67,9
						141,6
						104,7
						178,4
						104,7
						141,6
Итого

Система нормальных уравнений будет иметь вид:

.

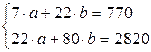Решив ее, получим:

.

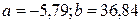Запишем уравнение регрессии:

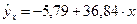
Подставив в уравнение значения , найдем теоретические значения 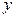(см. последнюю графу таблицы). В данном случае величина параметра не имеет экономического смысла.

В рассматриваемом примере имеем:

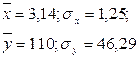
Коэффициент корреляции

Перейдем к оценке тесноты корреляционной зависимости. Рассмотрим наиболее важный для практики и теории случай линейной зависимости вида .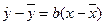

Представим уравнение 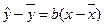в эквивалентном виде:

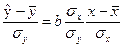
В этой системе величина

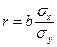(2.14)

показывает, на сколько величин s_у изменится в среднем 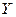, когда 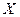увеличится на одно s_х.

Величина 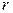является показателем тесноты линейной связи и называется выборочным коэффициентом корреляции (или просто коэффициентом корреляции).

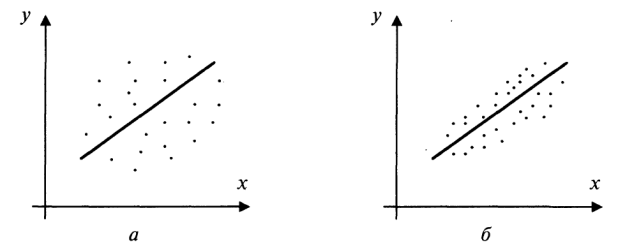
Две корреляционные зависимости переменной 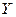от 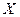приведены на рис. Очевидно, что в случае а) зависимость между переменными менее тесная и коэффициент корреляции должен быть меньше, чем в случае б), так как точки корреляционного поля а) дальше отстоят от линии регрессии, чем точки поля б).

Если 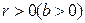, то корреляционная связь между переменными называется прямой, если 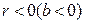, - обратной. При прямой (обратной) связи увеличение одной из переменных ведет к увеличению (уменьшению) условной (групповой) средней другой.

Учитывая (2.13), формулу для 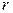представим в виде:

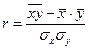(2.15)

Отметим другие модификации формулы 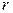, полученные из формулы (2.15):

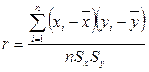(2.16)

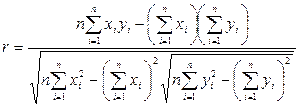(2.17)

Для практических расчетов наиболее удобна формула (2.17), так как по ней 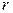находится непосредственно из данных наблюдений и на значении 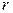не скажутся округления данных, связанные с расчетом средних и отклонений от них.

Выборочный коэффициент корреляции 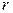(при достаточно большом объеме выборки 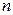) так же, как и коэффициент корреляции двух случайных величин, обладает следующими свойствами.

1. Коэффициент корреляции принимает значения на отрезке [– 1;1], т.е. 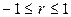. Чем ближе 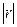к единице, тем теснее связь.

2. При 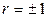корреляционная связь представляет линейную функциональную зависимость. При этом все наблюдаемые значения располагаются на прямой линии.

3. При 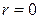линейная корреляционная связь отсутствует. при этом линия регрессии параллельна оси Ох.

Теорема Гаусса – Маркова

В силу воздействия неучтенных случайных факторов и причин отдельные наблюдения переменной 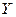будут в большей или меньшей мере отклоняться от функции регрессии .

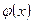Рассмотрим линейный регрессионный анализ, для которого линейная парная регрессионная модель имеет вид:

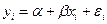. (2.18)

Отметим основные предпосылки регрессионного анализа.

1. В модели 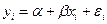возмущение 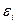(или зависимая переменная 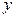) есть величина случайная, а объясняющая переменная 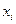- величина неслучайная.

2. Математическое ожидание возмущения 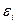равно нулю:

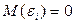(2.19)

(или математическое ожидание зависимой переменной 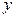равно линейной функции регрессии: ).

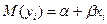3. Дисперсия возмущения 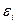(или зависимой переменной 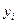) постоянна для любого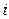

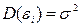(2.20)

(или 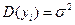) – условие гомоскедастичности или равноизменчивости возмущения (зависимой переменной )).

4. Возмущения 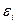и 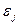(или переменные 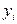и 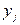) не коррелированы:

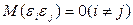(2.21)

5. Возмущение 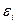(или зависимая переменная 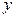) есть нормально распределенная случайная величина.

В этом случае модель 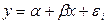называется классической нормальной линейной регрессионной моделью.

Для получения уравнения регрессии достаточно предпосылок 1 – 4. Требование выполнения предпосылки 5 (т.е. рассмотрение «нормальной регрессии») необходимо для оценки точности уравнения регрессии и его параметров.

Оценкой модели 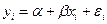по выборке является уравнение регрессии 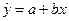. Параметры этого уравнения и определяются на основе метода наименьших квадратов.

Воздействие неучтенных случайных факторов и ошибок наблюдений в модели 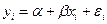определяется с помощью дисперсии возмущений (ошибок) или остаточной дисперсии 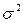. Несмещенной оценкой этой дисперсии является выборочная остаточная дисперсия.

S ² 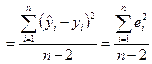, (2.22)

где 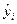– групповая средняя, найденная по уравнению регрессии; 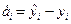– выборочная оценка возмущения 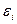или остаток регрессии.

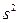Возникает вопрос, являются ли оценки , и параметров 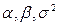«наилучшими»? Ответ на этот вопрос дает следующая теорема.

Теорема Гаусса – Маркова. Если регрессионная модель 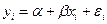удовлетворяет предпосылкам 1 – 4, то оценки , имеют наименьшую дисперсию в классе всех линейных несмещенных оценок.

Таким образом, оценки , в определенном смысле являются наиболее эффективными линейными оценками параметров , .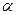

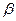Коэффициент детерминации

Проверить значимость уравнения регрессии – значит установить, соответствует ли математическая модель, выражающая зависимость между переменными, экспериментальным данным и достаточно ли включенных в уравнение объясняющих переменных (одной или нескольких) для описания зависимой переменной.

Проверка значимости уравнения регрессии производится на основе дисперсионного анализа.

В математической статистике дисперсионный анализ рассмотрен как самостоятельный инструмент (метод) статистического анализа. Здесь же он применяется как вспомогательное средство для изучения качества регрессионной модели.

Согласно основной идее дисперсионного анализа общая сумма квадратов отклонений зависимой переменной от средней 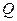представляется в виде:

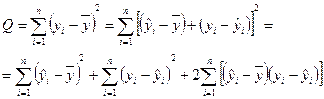(2.23)

или 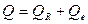, (2.24)

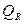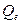где и – соответственно сумма квадратов, обусловленная регрессией, и остаточная сумма квадратов, характеризующая влияние неучтенных факторов и

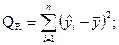
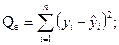(2.24)

Легко убедиться в том, что в (2.23) третье слагаемое 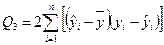равно 0 (см. [1], с.70).

Схема дисперсионного анализа имеет вид, представленный в таблице.

Компоненты регрессии	Сумма квадратов	Число степеней свободы	Средние квадраты
Регрессия		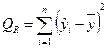m – 1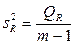
Остаточная		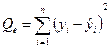n – m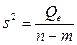
Общая		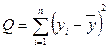n – 1

Средние квадраты 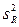, 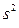представляют собой несмещенные оценки дисперсий зависимой переменной, обусловленных соответственно регрессией или объясняющей переменной 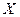и воздействием неучтенных случайных факторов и ошибок; m – число оцениваемых параметров уравнения регрессии; n – число наблюдений.

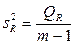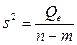При отсутствии линейной зависимости между зависимой и объясняющими(ей) переменными случайные величины и имеют 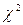– распределение соответственно с m – 1 и n – m степенями свободы, а их отношение – 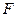-распределение с теми же степенями свободы. Поэтому уравнение регрессии значимо на уровне 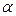, если фактически наблюдаемое значение статистики

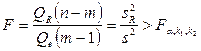, (2.24)

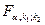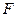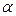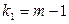где – табличное значение -критерия Фишера-Снедекора, определенное на уровне значимости при и 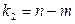степенях свободы.

Учитывая смысл величин 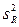и 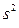, можно сказать, что значение 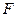показывает, в какой мере регрессия лучше оценивает значение зависимой переменной по сравнению с ее средней.

В случае линейной парной регрессии 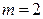, и уравнение регрессии значимо на уровне 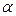, если

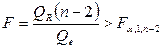. (2.25)

Иначе, гипотеза 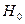о равенстве параметра нулю, т.е. 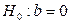, отвергается.

Одной из наиболее эффективных оценок адекватности регрессионной модели, мерой качества уравнения регрессии, (или, как говорят, мерой качества подгонки регрессионной модели к наблюденным значениям 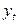), характеристикой прогностической силы анализируемой регрессионной модели является коэффициент детерминации, определяемый по формуле:

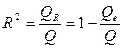. (2.26)

Величина 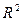показывает, какая часть (доля) вариации зависимой переменной обусловлена вариацией объясняющей переменной.

Так как 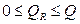, то .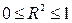

Чем ближе 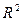к единице, тем лучше регрессия аппроксимирует эмпирические данные, тем теснее наблюдения примыкают к линии регрессии. Если 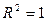, то эмпирические точки 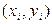лежат на линии регрессии и между переменным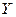и и 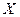существует линейная функциональная зависимость. Если 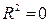, то вариация зависимой переменной полностью обусловлена воздействием неучтенных в модели переменных, и линия регрессии параллельна оси абсцисс.

Если известен коэффициент детерминации 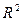, то критерий значимости (2.24) уравнения регрессии или самого коэффициента детерминации может быть записан в виде:

.

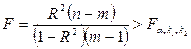В случае парной линейной регрессионной модели коэффициент детерминации равен квадрату коэффициента корреляции, т.е. .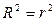

По модели парной регрессии

В прогнозных расчетах по уравнению регрессии определяется предсказуемое 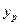значение как точечный прогноз 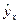при подстановки в линейное уравнение регрессии 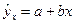соответствующего значения 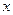. Однако точечный прогноз явно нереален, поэтому он дополняется расчетом стандартной ошибки 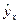, т.е. 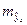, и соответственно мы получаем интервальную оценку прогнозного значения :

.

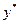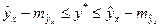Для того чтобы понять, как строится формула для определения величин стандартной ошибки 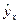, подставим в уравнение линейной регрессии выражение параметра :

,

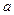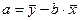тогда уравнение регрессии примет вид:

.

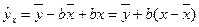Отсюда следует, что стандартная ошибка 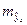зависит от ошибки 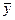и ошибки коэффициента регрессии 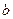, т.е.

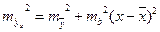. (2.27)

Считая, что прогнозное значение фактора 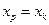, получим следующую формулу расчета стандартной ошибки предсказываемого по линии регрессии значения, т.е. :

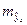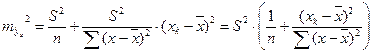. (2.28)

Соответственно 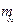имеет выражение:

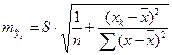. (2.29)

Рассмотренная формула стандартной ошибки предсказываемого среднего значения 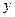при заданном значении 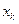характеризует ошибку положения линии регрессию. Величина стандартной ошибки 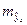достигает минимума при