Вычисление скоростей точек тела, совершающего плоскопараллельное движение

В любой момент времени скорости любых двух точек плоской фигуры и связаны равенством

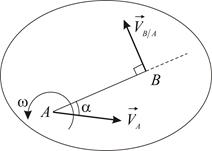Рис. 2.3

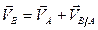(a)

Вектор 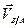представляет собой скорость, полученную точкой при вращении плоской фигуры вокруг оси, проходящей через полюс перпендикулярно плоской фигуре. Этот вектор направлен перпендикулярно отрезку 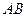(по касательной к окружности, которую описывает точка при вращении тела вокруг оси 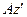), причем в сторону вращения тела (Рис. 2.3). В соответствии с формулой Эйлера

Пример 2.4

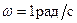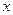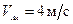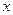Пластина совершает плоскопараллельное движение. В данный момент времени угловая скорость пластины равна , проекция на ось скорости точки пластины равна . Скорость точки образует с осью угол 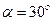(Рис. 2.4). Определить модули скоростей точек и , если .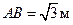

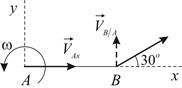Рис. 2.4

Запишем уравнение (a) в проекциях на координатные оси:

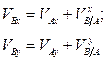или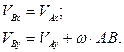

Учитывая данные задачи, получаем:

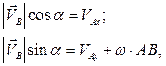или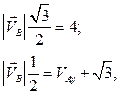

Отсюда:

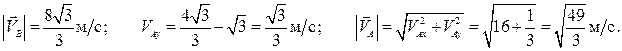
Следует заметить, что прямое использование формулы (a) целесообразно в довольно небольшом числе случаев. В некоторых задачах имеет смысл использовать так называемую теорему о проекциях. Поскольку вектор 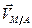перпендикулярен отрезку 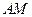, из формулы (a) получаем утверждение:

проекции скоростей концов отрезка, соединяющего две точки абсолютно твердого тела, на направление этого отрезка равны.

Пример 2.5

Стержень 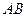движется в плоскости рисунка, причём его конец всё время находится на полуокружности 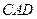, а сам стержень всё время касается неподвижного выступа 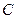, расположенного на диаметре 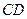(Рис. 2.5). Определить скорость 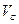точки стержня, касающейся выступа, в тот момент времени, когда радиус 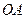перпендикулярен 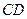, если известно, что скорость точки в этот момент .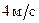

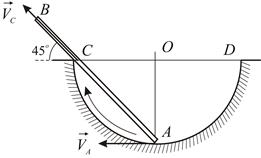Рис. 2.5

Заметим, что направления скоростей точек и 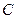в данный момент времени известны. Скорость точки направлена по касательной к траектории, т.е. по касательной к окружности в нижней точке. Скорость точки 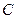направлена вдоль стержня, т.к. по условию задачи стержень не отрывается от выступа. Таким образом, для заданного положения стержня известны углы, которые образуют векторы скоростей точек и 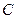с отрезком 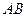. В таком случае целесообразно использовать теорему о проекциях скоростей:

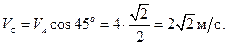
Решение задач с помощью мгновенного центра скоростей.Основной способ определения поля скоростей при плоскопараллельном движении твёрдого тела основан на использовании мгновенного центра скоростей.

Как уже говорилось, за полюс можно принять любую точку плоской фигуры. В данный момент времени различные точки тела имеют разные скорости. За полюс имеет смысл принимать точку, скорость которой в данный момент времени равна нулю.

Точка, принадлежащая плоской фигуре или неизменно с ней связанная, скорость которой в данный момент времени равна нулю, называется мгновенным центром скоростей.

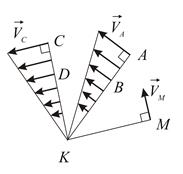Рис. 2.6

Скорость любой точки плоской фигуры определяется так же, как если бы тело вращалось вокруг оси, проходящей через мгновенный центр скоростей перпендикулярно плоскости движения плоской фигуры (Рис. 2.6):

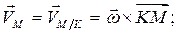
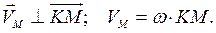
Пример 2.6

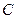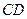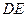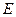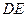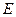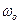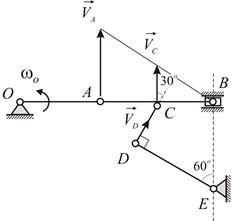
Кривошипн0-шатунный механизм связан шарнирно в середине шатуна со стержнем , а последний – со стержнем , который может вращаться вокруг оси . Определить угловую скорость стержня в указанном на Рис. 2.7 положении механизма, если точки и расположены на одной вертикали; угловая скорость кривошипа 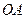равна 8 рад/с,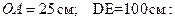

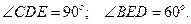
Рис. 2.7

Стержень 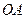вращается вокруг неподвижной оси. Скорость точки определяем по формуле Эйлера:

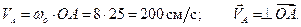
Движение стержня 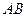плоскопараллельное. Мгновенный центр скоростей находится в точке . Учитывая, что скорости точек тела пропорциональны расстояниям до мгновенного центра скоростей, получаем:

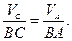Отсюда: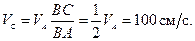

Движение стержня 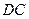плоскопараллельное. Скорость точки 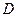направлена по касательной к окружности радиуса 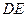, которая является траекторией точки 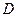. При заданном положении механизма направление скорости точки 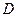совпадает с направлением стержня 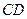. Для определения скорости точки 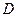имеет смысл использовать теорему о проекциях скоростей:

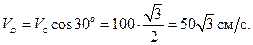
Остаётся определить угловую скорость стержня 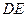. Поскольку движение этого стержня вращательное, используем формулу Эйлера:

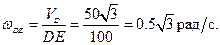
Пример 2.7

Колесо радиуса 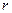катится без скольжения по неподвижной поверхности (Рис. 2.8). Скорость центра колеса 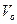. Определить скорости точек 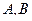и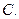

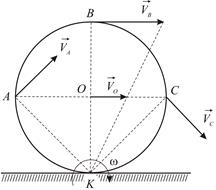Рис. 2.8

Мгновенный центр скоростей 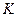находится в точке касания колеса и дороги. Зная скорость центра, находим угловую скорость колеса:

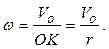
Скорости точек колеса определяем по формуле Эйлера:

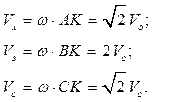
Качение колеса представляет интерес еще и в том отношении, что позволяет проиллюстрировать смысл формулы (a). Пусть колесо, движение которого мы рассматриваем, – ведущее колесо, т.е. оно принудительно вращается некоторым приводом. Рассмотрим возможные режимы движения.

Может случиться так, что колесо вращается, но автомобиль не перемещается – буксует. В этом случае движение колеса представляет собой вращение вокруг неподвижной оси 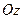. Все точки колеса будут описывать окружности с центром в точке 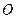, радиусы которых равны расстояниям от этих точек до оси колеса. Скорость любой точки направлена по касательной к этой окружности и определяется по формуле Эйлера.

Другое возможное движение колеса представляет собой качение с проскальзыванием. Автомобиль при этом перемещается, но колеса вращаются несоразмерно быстро. Скорость оси колеса отлична от нуля и вступает в свои права формула (a). Скорость, например, точки , которая в первом случае была ее полной скоростью, становится скоростью, полученной точкой при вращении колеса вокруг оси 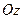. Полная же скорость точки теперь геометрически складывается из скорости точки 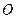и скорости, полученной точкой при вращении колеса вокруг оси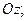

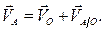
Заметим, что в этом случае движение оси (т.е. автомобиля) и вращение колеса происходят независимо друг от друга и каждое из них должно быть задано.

Последний режим движения колеса – качение без скольжения. Именно этот случай рассмотрен в примере 2.7. Движение оси и вращение колеса оказываются взаимосвязанными. В каждое мгновение очевидно положение точки, скорость которой равна нулю. В такой ситуации при определении скоростей точек колеса удобнее за полюс брать не точку 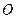, а мгновенный центр скоростей .

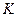ЗАДАЧИ, РЕКОМЕНДУЕМЫЕ ДЛЯ РАЗБОРА В АУДИТОРИИ И ДЛЯ ЗАДАНИЯ НА ДОМ:

Из сборника задач И.В.Мещерского: 16.3; 16.10; 16.15; 16.16; 16.19; 16.24; 16.28; 16.29; 16.31; 16.32; 16.33; 16.34; 16.35; 16.36; 16.38; 16.39.

Из учебника «ТЕОРЕТИЧЕСКАЯ МЕХАНИКА - теория и практика»: комплект СР-20.

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 6

Пример 2.8

Определить скорость и ускорение ползуна кривошипного механизма, а также угловую скорость и угловое ускорение шатуна 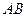в положении, изображенном на Рис. 2.9. Кривошип 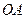вращается замедленно, имея в данный момент времени угловую скорость 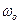и угловое ускорение 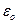. Ползун движется по криволинейной направляющей, имеющей в данном положении механизма радиус кривизны 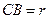. Дано: .

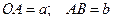Зная направления скоростей точек и , построим мгновенный центр скоростей 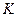стержня 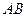, после чего определим угловую скорость стержня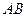

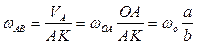
и скорость точки

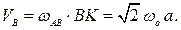
Попытка определить угловое ускорение стержня 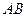, используя определение

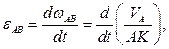
закончится неудачей, поскольку зависимость 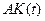неизвестна.

Для определения ускорения точки принимаем за полюс точку . Поскольку известны траектории всех точек во всех их движениях, представим ускорения точек их составляющими:

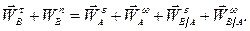
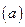
Вычислим векторы, входящие в уравнение .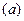

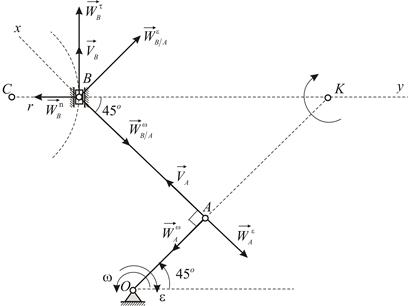Рис. 2.9

Точка принадлежит вращающемуся телу 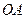. Определяем модули составляющих ускорения этой точки:

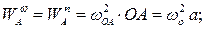
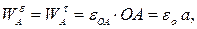
направления векторов показаны на Рис. 2.9.

Точка движется по криволинейной направляющей. Касательное и нормальное ускорения точки определяются по формулам:

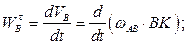
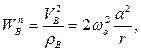
направления составляющих ускорения показаны на Рис. 2.9. По приведенной формуле не удается вычислить касательное ускорение точки , поскольку неизвестны зависимости расстояни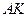й и 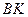от времени.

Находим составляющие ускорения, полученного точкой при вращении шатуна 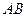вокруг оси 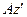. Заметим, что вращательное ускорение остается неизвестным по модулю, поскольку неизвестно угловое ускорение шатуна:

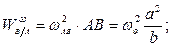
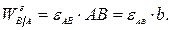
Таким образом, из шести векторов, входящих в равенство 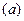, только два неизвестны по модулю. Определим эти неизвестные из уравнения 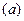. Это уравнение можно решить аналитически или геометрически. Рассмотрим оба способа решения.

Имеет смысл выбрать координатные оси так, чтобы в каждое уравнение в проекциях входила только одна неизвестная. Направим ос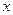ь вдоль 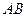(перпендикулярно 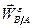), а ось 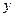по направлению 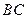(перпендикулярно 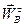). Записывая уравнение 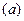в проекциях на ось 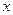, получаем:

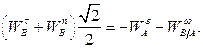
Отсюда

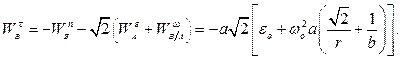
Отрицательный знак говорит о том, что предполагаемое направление вектора 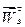было выбрано ошибочно; в действительности этот вектор направлен в противоположную сторону.

Записывая уравнение 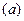в проекциях на ось 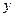, получаем:

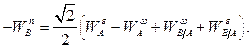
Отсюда

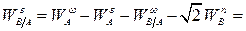
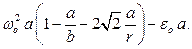
Рис. 2.10

Вычислив 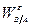, можем определить угловое ускорение стержня :

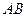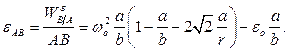
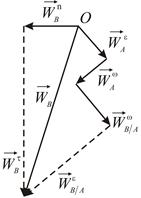
Рассмотрим геометрический способ решения уравнения 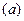. Построим в масштабе сумму векторов, стоящих в правой части уравнения 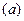. От некоторой точки 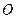отложим 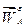, от его конца отложим 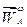, а затем 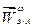(Рис. 2.10). Остается построить 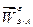, модуль которого неизвестен. Проведем через конец 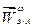пунктирную прямую, параллельную 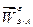. Конец суммы векторов, стоящих в правой части уравнения 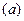, лежит на этой прямой.

Обратимся к левой части уравнения 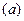. Отложим от точки 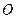известный вектор 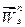. Через его конец проведем пунктирную прямую, параллельную вектору 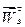. Точка пересечения построенных прямых определяет положение конца вектора ускорения точки .

Пример 2.9

Колесо радиуса 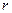катится без скольжения по прямолинейному пути (Рис. 2.11). Ось колеса движется ускоренно, имея в данный момент времени скорость 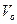и ускорение 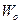. Определить проекции ускорение любой точки обода колеса на оси координат.

Принимая за полюс точку 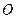, получаем:

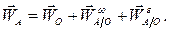
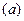
причем

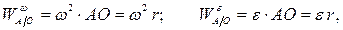
где 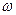– угловая скорость колеса; 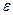– его угловое ускорение.

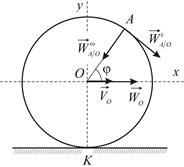Рис. 2.11

Зная положение мгновенного центра скоростей колеса – точка касания колеса и дороги, определяем угловую скорость колеса:

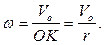
В рассматриваемой задаче расстояние от точки 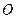, скорость которой известна, до мгновенного центра скоростей 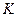со временем не изменяется. Это обстоятельство позволяет найти угловое ускорение колеса в данный момент времени по определению углового ускорения:

,

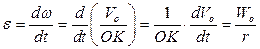так как 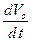представляет собой проекцию вектора ускорения точки 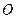на направление её вектора скорости, которая в рассматриваемом случае равна .

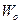Записывая уравнение 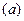в проекциях на координатные оси, получаем проекции вектора ускорения точки :

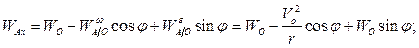
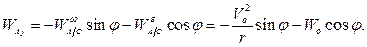
Пример 2.10

Колесо радиуса 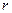катится без скольжения по криволинейной поверхности (Рис.2.12). Ось колеса движется ускоренно, имея в данный момент времени скорость 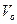и касательное ускорение 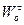. Определить проекции ускорения любой точки обода колеса на заданные координатные оси, если радиус кривизны в точке 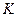равен .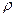

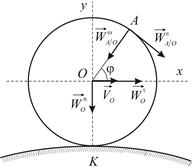Рис. 2.12

Задача решается так же, как в примере 2.9, но в отличие от предыдущей задачи, траектория точки 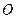– кривая линия. У точки 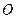появляется вторая составляющая ускорения – нормальная:

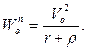
В результате получаем:

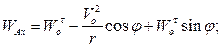
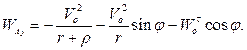
Пример 2.11

Колесо радиуса 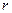катится без проскальзывания по прямолинейному пути. Ось колеса движется равномерно со скоростью 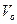(Рис. 2.13). Определить ускорение любой точки колеса.

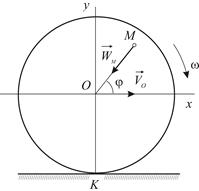Рис. 2.13

Ось колеса движется равномерно и прямолинейно. Следовательно, точка 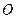– мгновенный центр ускорений. Для любой точки колеса получаем:

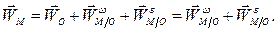
Но угловая скорость колеса 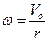постоянна и, следовательно, угловое ускорение колеса равно нулю.

Тогда

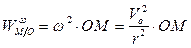
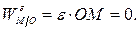
Таким образом, ускорение любой точки совпадает с осестремительным ускорением, полученным этой точкой при вращении колеса вокруг оси, проходящей через центр колеса 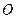перпендикулярно плоскости движения.

ЗАДАЧИ, РЕКОМЕНДУЕМЫЕ ДЛЯ РАЗБОРА В АУДИТОРИИ И ДЛЯ ЗАДАНИЯ НА ДОМ:

Из сборника задач И.В.Мещерского: 18.11; 18.13; 18.16; 18.18; 18.22; 18.23; 18.25; 18.26; 18.28; 18.37; 18.38; 18.39; 18.40.

Из учебника «ТЕОРЕТИЧЕСКАЯ МЕХАНИКА - теория и практика»: комплекты СР-21;

СР-22.

ПРАКТИЧЕСКИЕ ЗАНЯТИЯ № 7-8

СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ