Определение радиуса кривизны траектории по заданным уравнениям движения точки

Рассмотрим алгоритм решения такой задачи. Пусть движение точки задано в координатной форме:

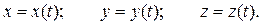
Для определения радиуса кривизны траектории необходимо вычислить квадрат скорости точки и её нормальное ускорение:

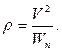
Квадрат полного ускорения точки вычисляем по формуле:

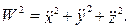
Учитывая, что нормальная и касательная составляющие ускорения взаимно перпендикулярны, находим

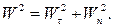Отсюда: .

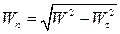Квадрат скорости точки определяем по формуле:

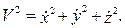
Для определения касательного ускорения продифференцируем по времени последнее соотношение:

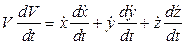или

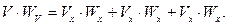
Здесь 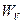– проекция вектора ускорения на направление вектора скорости. Заметим, что .

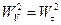Пример 1.7

Движение точки задано уравнениями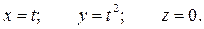

Определить радиус кривизны траектории для любого момента времени.

Вычислим квадрат скорость точки: .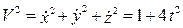

Вычислим квадрат ускорения точки: .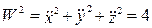

Равенство 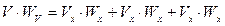принимает вид: .

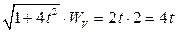Отсюда:

.

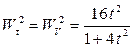Нормальное ускорение равно

.

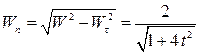Определяем радиус кривизны траектории

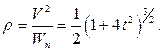
Пример 1.8

Определить радиус кривизны траектории снаряда, движение которого описано в примере 1.2.

Применительно к задаче о движении снаряда получаем:

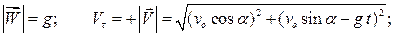
Заметим, что направление движения снаряда по траектории со временем не изменяется. Направим орт касательной по направлению вектора скорости. Тогда проекция вектора скорости на направление орта касательной к траектории положительна в любой момент времени.

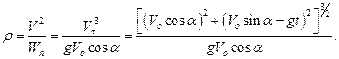
ЗАДАЧИ, РЕКОМЕНДУЕМЫЕ ДЛЯ РАЗБОРА В АУДИТОРИИ И ДЛЯ ЗАДАНИЯ НА ДОМ:

Из сборника задач И.В.Мещерского: 10.4; 12.1; 12.6; 12.7; 12.9; 12.10.

Из учебника «ТЕОРЕТИЧЕСКАЯ МЕХАНИКА - теория и практика»: комплекты СР-17;

СР-18: СР-19.

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 3

КИНЕМАТИКА ТВЁРДОГО ТЕЛА

Простейшие движения твёрдого тела

Пример 2.1

Угол наклона полного ускорения точки обода махового колеса к радиусу 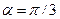. Касательное ускорение этой точки в данный момент времени 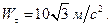Найти нормальное ускорение точки, отстоящей от оси вращения на расстоянии 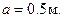Радиус махового колеса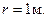

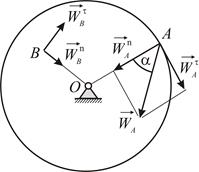Рис. 2.1

Нормальное ускорение точки направлено по радиусу (Рис. 2.1), следовательно,

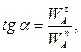Отсюда: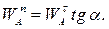

Используя формулы,

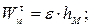
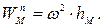
получаем:

;

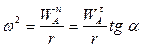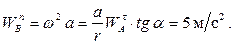
Пример 2.2

Вал радиуса 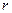приводится во вращение гирей, прикрепленной к концу троса, намотанного на вал. Определить модуль ускорения точки обода вала, если ускорение гири 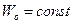(Рис.2.2). В начальный момент вал находился в покое.

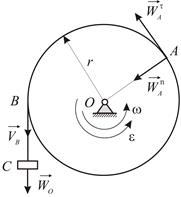Рис. 2.2

Точки троса, покинув поверхность вала, движутся прямолинейно равноускоренно:

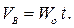
Поскольку трос не проскальзывает по поверхности вала, скорости точек троса и вала совпадают.

Используя формулу Эйлера, находим угловую скорость вала

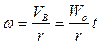
и его угловое ускорение

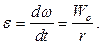
Теперь определяем составляющие ускорения любой точки обода вала:

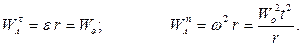
Остается определить модуль ускорения точки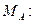

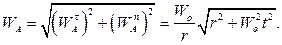
Заметим, что если скорости точек троса и вала совпадают, то их ускорения различны: точка вала имеет нормальную составляющую ускорения, поскольку движется по криволинейной траектории.

Пример 2.3

Стрелка гальванометра длиной 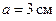колеблется вокруг неподвижной оси по закону 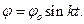Определить ускорение конца стрелки в ее среднем и крайних положениях, если период колебаний 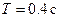, а угловая амплитуда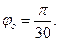

Прежде всего, зная закон вращения, определим угловую скорость и угловое ускорение тела:

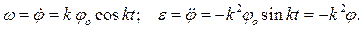
Используя формулы (2.3), определяем касательное и нормальное ускорения точки:

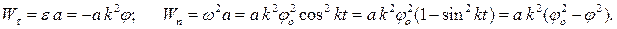
Период связан с круговой частотой соотношением 2 .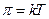

Для среднего положения стрелки имеем:

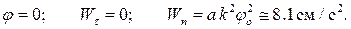
Для крайних положений стрелки имеем:

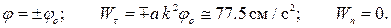
ЗАДАЧИ, РЕКОМЕНДУЕМЫЕ ДЛЯ РАЗБОРА В АУДИТОРИИ И ДЛЯ ЗАДАНИЯ НА ДОМ:

Из сборника задач И.В.Мещерского: 13.6; 13.14; 13.17; 13.18; 14.4; 14.5; 14.10.

ПРАКТИЧЕСКИЕ ЗАНЯТИЯ № 4-5