Введение в кинематику твердого тела

ЛЕКЦИЯ 1 (5)

Кинематика – один из разделов курса теоретической механики, в котором рассматривается движение тел без учета причин, приводящих к изменению этого движения, т.е. без учета сил.

Под движением в механике понимаем изменение с течением времени положения тела в пространстве по отношению к другим телам. Это означает, что изучая движение какого–либо тела, необходимо указать другое тело — тело отсчета, по отношению к которому рассматривается движение. С телом отсчета жестко связана система координат. Тело отсчета, связанная с ним система координат и счетчик времени — часы образуют систему отсчета. Поскольку в классической механике считается, что время не зависит от движения тел и одинаково во всех точках пространства и во всех системах отсчета, то, говоря о системе отсчета, обычно задают только тело отсчета, а еще чаще, только систему координатных осей, связанных с телом отсчета.

Положение точки или тела по отношению к выбранной системе отсчета определяется некоторыми параметрами — координатами. Движение будет задано, если известен закон, по которому эти координаты изменяются с течением времени. Разработка методов, при помощи которых может быть задано движение точки или тела — одна из задач кинематики. Другая задача кинематики состоит в том, чтобы зная закон движения точки или тела, определить кинематические величины, характеризующие движение (скорости, ускорения и т.д.).

Движение точки по отношению к выбранной системе отсчета считается заданным, если известен способ, при помощи которого можно определить положение точки в любой момент времени.

КИНЕМАТИКА ТОЧКИ

1.1. Координатный способ задания движения точки

Положение точки в системе отсчета полностью определяется ее координатами. Если известна зависимость координат от времени, движение точки считается заданным. В зависимости от содержания решаемой задачи можно использовать любую систему координат (декартову, цилиндрическую, сферическую и т.д.), наиболее целесообразную для решения данной задачи. Мы, в основном, будем использовать прямоугольную декартову систему

Рис. 1.1

координат, в которой законы движения точки имеют вид:

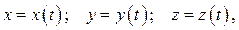(1.1)

где 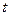– время.

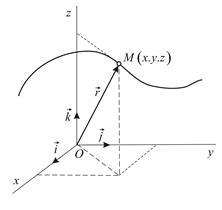
Вектор 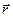, проведенный из начала координат в точку , называется радиусом–вектором точки. Координаты точки одновременно являются проекциями радиуса–вектора на координатные оси (Рис. 1.1):

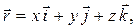(1.2)

где 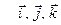– единичные векторы (орты) координатных осей.

Непрерывная кривая, которую описывает точка при своем движении, называется траекторией точки.

Уравнения (1.1) представляют собой уравнения траектории в параметрической форме, где роль параметра играет время 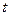. Придавая параметру 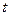ряд последовательных значений, начиная с нуля, например, с интервалом в одну секунду, получаем ряд последовательных положений точки в пространстве или на плоскости. Соединяя построенные точки плавной кривой, получаем траекторию. Очевидны недостатки такого способа построения траектории. С одной стороны, он достаточно трудоемок, а с другой стороны, его точность зависит от выбранного для вычислений временного интервала.

Намного удобнее получить уравнение траектории в координатной форме. Для этого необходимо из уравнений движения (1.1) исключить параметр 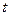. При этом следует учитывать только те значения координат, которые соответствуют неотрицательным значениям параметра .

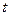Пример

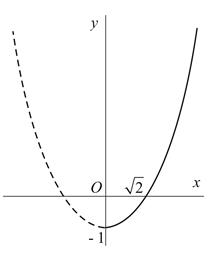Рис.1.2

Даны законы движения точки в координатной форме:

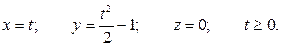
Определить траекторию точки.

Исключая время из уравнений движения, получаем уравнение параболы:

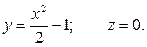
Однако, уравнения движения и заданный интервал времени налагают ограничения на область допустимых значений координат:

при 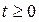имеем:

Таким образом, траекторией будет только правая ветвь параболы (Рис. 1.2).

Скорость точки

Быстроту движения точки характеризует ее скорость, к определению которой мы сейчас переходим.

Пусть в момент времени 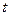точка находится в положении , которое определяется радиусом-вектором 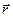, а в момент 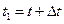переходит в положение 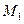, радиус–вектор которого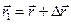

(Рис. 1.3). Вектор 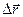называется вектором перемещения точки за время 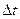. Если разделить вектор перемещения на 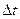, получим вектор того же направления, что и 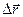, который определяет среднюю по модулю и направлению скорость точки за время .

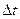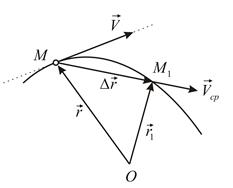Рис.1.3

Понятно, что средняя скорость зависит от выбранного промежутка времени и тем точнее характеризует быстроту движения, чем меньшим выбран промежуток времени .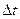

Скоростью точки в данный момент времени называется предел отношения вектора перемещения к промежутку времени, за который это перемещение произошло, при величине промежутка времени, стремящейся к нулю:

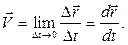(1.3)

Таким образом,

вектор скорости равен первой производной по времени от радиуса-вектора точки.

В пределе при 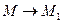секущая 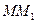, по которой направлена средняя скорость, занимает положение касательной к траектории в точке . Следовательно,

вектор скорости направлен по касательной к траектории, причем в сторону движения точки.

Пусть движение точки задано в координатной форме, т.е. уравнениями (1.1). Используя равенство (1.2) и учитывая, что орты координатных осей со временем не изменяются, получаем:

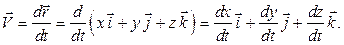
Таким образом, проекции вектора скорости на оси координат равны первым производным по времени от соответствующих координат точки:

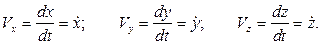(1.4)

Ускорение точки

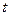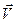Быстроту изменения вектора скорости характеризует ускорение точки. Пусть в момент времени точка находится в положении и имеет скорость , а в момент 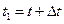, переходит в положение 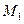и имеет скорость 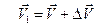(Рис. 1.4).

Ускорением точки называется предел отношения приращения вектора скорости к промежутку времени, за который это приращение произошло, при величине промежутка времени, стремящейся к нулю:

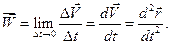(1.5)

Таким образом,

ускорение точки равно первой производной по времени от вектора скорости точки или второй производной по времени от радиуса-вектора точки.

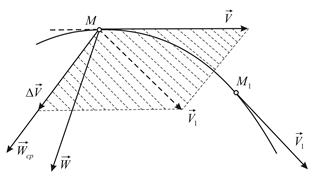Рис.1.4

Если траектория – плоская кривая, то вектор ускорения лежит в плоскости этой кривой и направлен в сторону ее вогнутости. Если траектория – пространственная кривая, то при предельном переходе 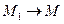плоскость, содержащая вектор среднего ускорения (на чертеже заштрихована), будет поворачиваться вокруг вектора 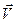и в пределе займет положение, которое называется соприкасающейся плоскостью к траектории в точке . Таким образом,

вектор ускорения точки лежит в соприкасающейся к траектории в данной точке плоскости, причем направлен в сторону вогнутости траектории.

Пусть движение точки задано в координатной форме, т.е. уравнениями (1.1). Тогда

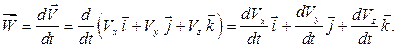
Таким образом, проекции вектора ускорения на координатные оси равны первым производным по времени от соответствующих проекций вектора скорости или, учитывая равенства (5.4), вторым производным по времени от соответствующих координат точки:

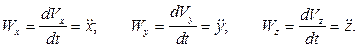(1.6)

ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ

1. Что называется радиусом-вектором точки?
2. В чём состоит координатный способ задания движения точки?
3. Что называется траекторией точки?
4. Что называется скоростью точки?
5. Как вычисляется вектор скорости при координатном способе задания движения?
6. Как располагается вектор скорости по отношению к траектории?
7. Что называется ускорением точки?
8. Как вычисляется вектор ускорения при координатном способе задания движения?
9. Как располагается вектор ускорения по отношению к траектории?

ЛЕКЦИЯ 2 (6)

1.4. Естественный способ задания движения точки

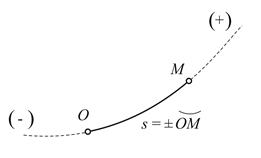Рис. 1.5

Пусть траектория точки заранее известна. Рассматривая траекторию как криволинейную координатную ось, примем любую точку 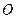траектории за начало отсчета и установим положительное и отрицательное направления отсчета.

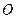Положение точки однозначно определяется дуговой координатой, которая равна взятой с соответствующим знаком длине дуги траектории, отделяющей в данный момент времени точку от начала отсчета (Рис. 1.5). Движение точки будет задано, если задана зависимость дуговой координаты от времени: 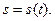Описанный способ задания движения называется естественным.

Пример

Точка движется по окружности радиуса 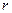(Рис. 1.6а). Дуговая координата изменяется по закону 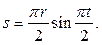Начало и направление отсчета координаты 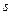указаны на чертеже. Проанализировать движение точки при .

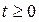Имеет смысл для наглядности построить график движения (Рис. 1.6б). Как видно из графика, точка начинает движение из начала отсчета дуговой координаты в положительном направлении (обход окружности против хода часовой стрелки). В этом направлении точка движется в течение одной секунды, за которую она успевает пройти дугу 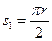, что составляет четверть длины окружности.

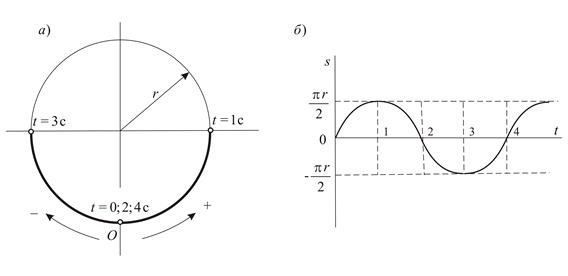Рис. 1.6

Затем дуговая координата начинает убывать, т.е. точка движется в противоположную сторону (к началу отсчета). При 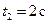дуговая координата обращается в нуль, т.е. точка попадает в начало отсчета 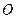. Далее дуговая координата становится отрицательной, возрастая по модулю, т.е. точка удаляется от точки 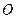в отрицательном направлении отсчета (по ходу часовой стрелки). К моменту 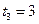с это удаление становится максимальным, равным четверти длины окружности.

Затем дуговая координата начинает возрастать. Точка снова поменяла направление движения и в момент 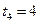с приходит в начало отсчета .

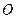После этого движение повторяется. Заметим, что траекторией точки в рассматриваемом случае будет только половина окружности (ее нижняя часть).

1.5. Естественный трехгранник. Вычисление скорости и ускорения при естественном способе задания движения

Пусть точка движется по траектории 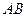, на которой установлена криволинейная система отсчета (Рис. 1.7).

В любой точке траектории существует единственная касательная. Обозначим 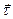единичный вектор касательной; направлен 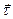в сторону возрастания дуговой координаты. Нормаль, лежащая в соприкасающейся плоскости, называется главной нормалью. Обозначим 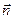единичный вектор главной нормали; 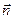направлен в сторону вогнутости траектории. Нормаль, перпендикулярная соприкасающейся плоскости, называется бинормалью. Ее единичный вектор 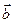направлен так, чтобы векторы 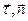и 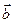образовывали правую тройку.

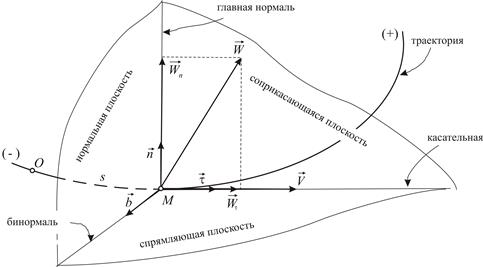Рис. 1.7

Соприкасающаяся, нормальная и спрямляющая плоскости образуют естественный трехгранник. Касательная, главная нормаль и бинормаль – оси естественного трехгранника; 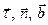– орты этих осей.

Оси естественного трехгранника играют существенную роль в описании движения точки, поскольку в этих осях вектор скорости и вектор ускорения вычисляются наиболее удобным образом. Разложение этих векторов по осям естественного трехгранника имеет вид:

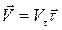(1.7)

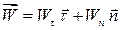(1.8)

где

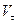– проекция вектора скорости на направление касательной к траектории;

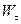– проекция вектора ускорения на направление касательной к траектории, ее называют касательным ускорением точки;

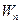– проекция вектора ускорения точки на направление главной нормали к траектории точки, ее называют нормальным ускорением точки.

Не останавливаясь на выводе формул, приведём конечные результаты для векторов скорости и ускорения точки.

Проекция вектора скорости на направление касательной к траектории точки равна первой производной по времени от дуговой координаты:

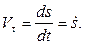(1.9)

Таким образом,

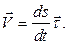(1.10)

Касательное и нормальное ускорения точки определяются по формулам:

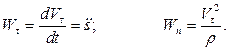(1.11)

Таким образом, вектор ускорения точки в естественных осях представляется в виде:

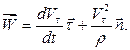(1.12)

Рис. 1.8

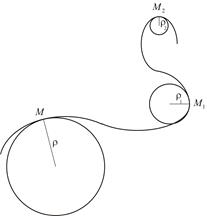
где 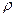– радиус кривизны траектории в точке . Не претендуя на строгость, попробуем пояснить это понятие. Среди линий постоянной кривизны особое место занимает окружность. Рассмотрим любую гладкую кривую (Рис. 1.8). Радиусом кривизны кривой в данной точке называется радиус окружности, дуга которой в малой окрестности точки совпадает с дугой заданной кривой. Заметим, что прямая также является кривой с постоянной кривизной. В каждой точке прямой радиус кривизны равен бесконечности ( ).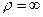

Как известно, производная по времени от какой-либо величины характеризует быстроту изменения со временем дифференцируемой величины. Ускорение характеризует изменение со временем вектора скорости. Вектор скорости может изменять со временем свой модуль и направление. Заметим, что касательное ускорение характеризует изменение модуля скорости, а нормальное – изменение направления скорости. Единственное движение, при котором ускорение точки равняется нулю это равномерное прямолинейное движение. При любом неравномерном движении отлично от нуля касательное ускорение; при любом криволинейном движении отлично от нуля нормальное ускорение.

КИНЕМАТИКА ТВЁРДОГО ТЕЛА

ЛЕКЦИЯ 3 (7)

Плоскопараллельное движение твердого тела. Задание движения

Движение тела называется плоскопараллельным, если расстояние от любой точки тела до некоторой неподвижной (основной) плоскости остается неизменным во все время движения

Проведем сечение тела параллельное основной плоскости (Рис. 2.6). Через любую точку сечения проведем отрезок 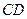, перпендикулярный основной плоскости. Из определения плоскопараллельного движения следует, что отрезок 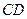движется поступательно. Таким образом, движение сечения полностью определяет плоскопараллельное движение тела.

Рассмотрим движение сечения (плоской фигуры) в своей плоскости (Рис. 2.7). Пусть любая точка плоской фигуры. Примем точку за начало системы координат 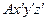, оси которой движутся поступательно по отношению к основной системе 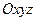. По отношению к системе 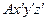плоская фигура может только вращаться вокруг подвижной оси .

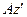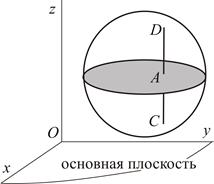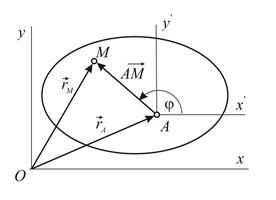Рис. 2.6		Рис. 2.7

Чтобы задать положение плоской фигуры, а следовательно, и всего тела, необходимо задать положение точки – полюса, а также задать вращение плоской фигуры по отношению к системе 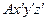. Таким образом, закон плоскопараллельного движения тела имеет вид:

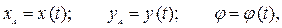
т.е. при плоскопараллельном движении тело имеет три степени свободы. Как видно, два первых уравнения описывают поступательную часть плоского движения, а последнее уравнение описывает вращение тела вокруг оси, проходящей через полюс .

Вычисление скорости любой точки тела. Вычислим скорость любой точки тела. В любой момент времени имеет место равенство (Рис. 2.7)

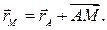
Тогда

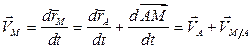(2.4)

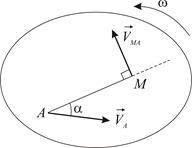Рис. 2.8

Вектор 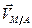представляет собой скорость, полученную точкой при вращении плоской фигуры вокруг оси 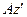. Этот вектор направлен перпендикулярно отрезку 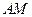(по касательной к окружности, которую описывает точка при вращении тела вокруг оси 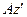), причем в сторону вращения тела (Рис. 2.8). Модуль скорости определяется по формуле Эйлера: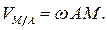

Поскольку вектор 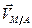перпендикулярен отрезку 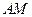, из формулы (6.4) получаем полезное для практических целей утверждение, которое обычно называют теоремой о проекциях:

проекции скоростей концов отрезка, соединяющего две точки абсолютно твердого тела, на направление этого отрезка равны.

Мгновенный центр скоростей. Как уже говорилось, за полюс можно принять любую точку плоской фигуры. В данный момент времени различные точки тела имеют разные скорости. За полюс имеет смысл принимать точку, скорость которой в данный момент времени равна нулю.

Рис. 2.9

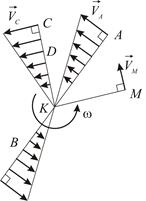
Точка, принадлежащая плоской фигуре или неизменно с ней связанная, скорость которой в данный момент времени равна нулю, называется мгновенным центром скоростей.

Примем за полюс мгновенный центр скоростей 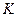. В соответствии с формулой (3.1), получаем, что скорость любой точки плоской фигуры определяется так же, как если бы тело вращалось вокруг оси 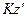(Рис. 2.9):

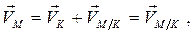так как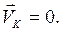

Рассмотрим способы определения положения мгновенного центра скоростей.

1. Пусть известны направления скоростей двух точек и плоской фигуры, причем вектор 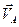не параллелен вектору 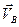. Как видно из Рис. 3.4, в этом случае мгновенный центр скоростей лежит в точке пересечения перпендикуляров, проведенных через точки и к векторам скоростей этих точек.

Рис. 2.10		Рис. 2.11

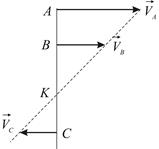
2. Пусть известны направления скоростей двух точек и , причем вектор 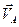параллелен вектору 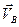, но отрезок 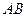не перпендикулярен скоростям (Рис. 2.10).

Проекции скоростей точек и на направление 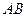, в соответствии с теоремой о проекциях, равны между собой 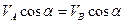и, следовательно, равны между собой векторы скоростей 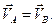Используя формулу (3.1) 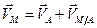, получаем

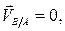т.е. 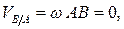отсюда: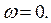

Таким образом, в данный момент времени угловая скорость тела равна нулю и скорости всех точек тела одинаковые. Имеем мгновенно поступательное распределение скоростей. Что касается положения мгновенного центра скоростей, то как видно из Рис. 6.11, перпендикуляры к скоростям оказываются параллельными. Можно считать, что мгновенный центр скоростей находится в бесконечно удаленной точке.

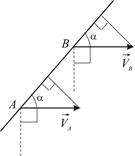
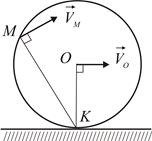
3. Пусть скорости точек и параллельны между собой и перпендикулярны отрезку 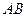(Рис. 2.11). В этом случае перпендикуляры к скоростям сливаются. Положение

Рис. 2.12

мгновенного центра скоростей 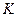на перпендикуляре 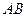можно определить из соображений пропорциональности модулей скоростей расстояниям от точек до мгновенного центра скоростей. Расстояние 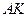можно определить из системы уравнений

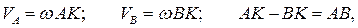
которую удобнее всего решить графически. Заметим, что в рассматриваемом случае для определения положения мгновенного центра скоростей кроме направления скоростей двух точек необходимо знать и их модули.

4. Особый интерес представляет случай качения колеса по неподвижной поверхности. Если колесо катится без проскальзывания, то мгновенный центр скоростей находится в точке касания колеса и опорной поверхности (Рис. 2.12).

Вычисление ускорений точек тела, совершающего плоскопараллельное движение. Ускорение любой точки плоской фигуры складывается из ускорения точки , принятой за полюс, и ускорения, полученного точкой при вращении плоской фигуры вокруг оси, проходящей через полюс перпендикулярно плоской фигуре:

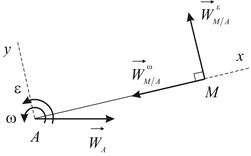Рис. 2.13

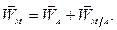(2.5)

Вектор 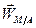удобно разложить на составляющие – на вращательное и осестремительное ускорения (Рис. 2.13):

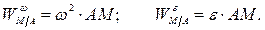
Уравнение (2.5) можно решать аналитически или геометрически. При аналитическом способе решения уравнение (2.5) записывают в проекциях на оси координат, одну из которых можно направить по прямой, соединяющей точки и , а вторую перпендикулярно :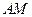

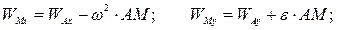
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ

1. Что называется плоскопараллельным движением твёрдого тела?

2. Из каких простейших движений складывается плоскопараллельное движение?

3. Как при плоскопараллельном движении связаны между собой скорости двух любых точек тела?

1. В чём состоит теорема о проекциях скоростей двух любых точек твёрдого тела?
2. Что называется мгновенным центром скоростей?

6. Как определяется положение мгновенного центра скоростей?

7. Как определить скорость точки при помощи мгновенного центра скоростей?

8. Как при плоскопараллельном движении связаны между собой ускорения двух любых точек тела?

ЛЕКЦИЯ 4 (8)

СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ

3.1. Основные определения

Часто возникает необходимость рассматривать движение точки одновременно по отношению к двум или более системам отсчета, движущимся относительно друг друга. В таком случае движение точки называется сложным.

Пусть система отсчета 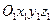условно неподвижна, а система 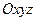движется по отношению к неподвижной произвольным, но известным образом (Рис. 3.1).

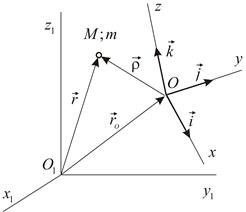Рис. 3.1

Движение точки по отношению к неподвижной системе отсчета называется абсолютным. Ее скорость и ускорение по отношению к неподвижной системе отсчета называются абсолютной скоростью 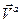и абсолютным ускорением .

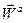Движение точки по отношению к подвижной системе отсчета называется относительным. Скорость и ускорение точки по отношению к подвижной системе отсчета называются относительной скоростью 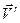и относительным ускорением .

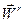Точки подвижного пространства 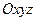совершают переносное для точки движение. Различные точки подвижного пространства имеют в данный момент времени в общем случае разные скорости и разные ускорения.

Переносной скоростью 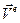и переносным ускорением 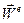точки называется скорость и ускорение той точки 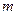подвижного пространства. в которой в данный момент времени находится движущаяся точка .

Связи между абсолютными, относительными и переносными скоростями и ускорениями устанавливаются соответствующими теоремами, для доказательства которых нам понадобятся некоторые вспомогательные положения.

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 1(9)

КИНЕМАТИКА ТОЧКИ

1.1. Координатный способ задания движения

Пример 1.1

Определить в интервале времени 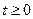траекторию точки шатуна 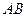кривошипно-шатунного механизма, если кривошип 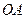вращается вокруг шарнира 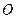так, что угол 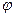изменяется по закону 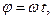где 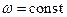(Рис.1.1). Дано: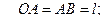

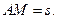
Вычислим координаты точки для произвольного положения механизма.

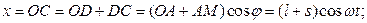
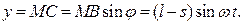
Для исключения параметра 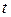воспользуемся основным тригонометрическим тождеством

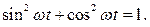
Возводя каждое из уравнений движения в квадрат

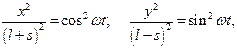
и складывая полученные уравнения, находим:

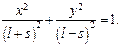
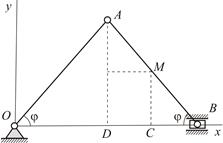Рис.1.1

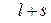Таким образом, точка движется по эллипсу с полуосями  и 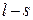 . При этом траекторией будет весь эллипс, поскольку он полностью укладывается в ограничения, получаемые из анализа кинематических уравнений движения: при 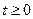имеем

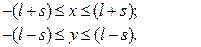
Рассмотренный в этом примере кривошипно-шатунный механизм широко используется в технике для преобразования поступательного движения во вращательное и наоборот. Как видно, этот механизм можно также использовать в качестве чертежного инструмента для построения эллипсов с заданными полуосям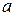и и 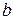. Достаточно подобрать величины 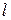и 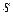так, чтобы выполнялись условия

Отсюда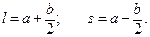

Пример 1.2

Снаряд движется в вертикальной плоскости. Угол наклона ствола орудия к горизонту 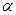. Начальная скорость снаряда 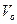. Определить траекторию снаряда, высоту и дальность обстрела, максимальную дальность обстрела. Сопротивлением воздуха пренебречь.

Заметим, что по условию задачи единственной силой, действующей на снаряд во время полета, является сила тяжести, которая сообщает снаряду ускорение свободного падения. Выбирая начало координат в точке расположения орудия и направляя ось 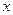горизонтально, а ось 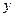вертикально (Рис.1.2), находим:

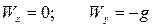или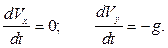

Получены обыкновенные дифференциальные уравнения первого порядка с разделяющимися переменными, интегрируя которые

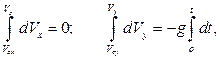
находим при заданных начальных условиях

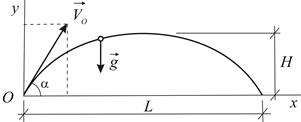Рис.1.2

законы изменения проекций скорости снаряда на координатные оси:

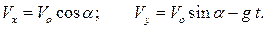(a)

Уравнения (a) можно рассматривать как дифференциальные уравнения относительно координат снаряда.

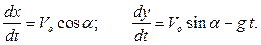
Выполняя интегрирование

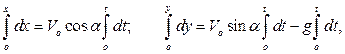
получаем закон движения снаряда:

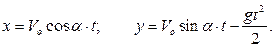(b)

Исключая время из уравнений (b) , получаем уравнение траектории снаряда:

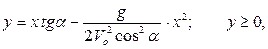
представляющей собой часть параболы, расположенную над осью .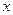

Обозначим 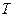время полета снаряда. Для момента падения снаряда имеем условия:

при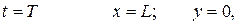

где 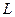– дальность полета снаряда. Подставляя эти условия в уравнения (b) , получаем

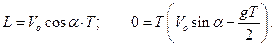
Отсюда

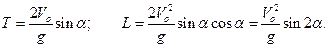
Очевидно, дальность будет максимальной, когда