Механическое взаимодействие горных пород и фильтрующейся жидкости при упругом режиме пластов

Перейдем, наконец, к важному вопросу механического взаимодействия горных пород и фильтрующейся жидкости при упругом режиме пластов. При рассмотрении деформации пород часто принимается, что движение жидкостей в горных породах является установившимся или квазиустановившимся (в каждый произвольно взятый момент времени распределение давления является различным, но соответствующим установившемуся течению). Строго говоря, это не так. На движение жидкости, насыщающей горные породы оказывает влияние деформация пород — в этом, собственно, и заключается одна из особенностей упругого режима нефтеводоносных пластов.

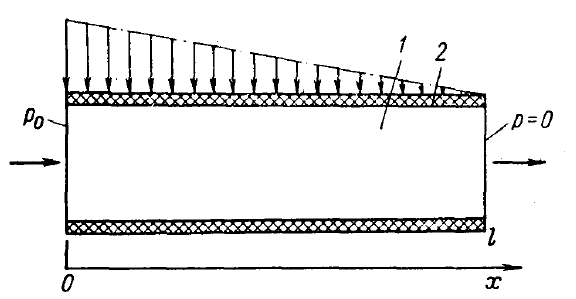
Рисунок 7.9 – Действие на пористую среду внешних усилий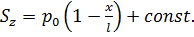

1 – образец; 2 – гибкая непроницаемая оболочка

Прежде всего, необходимо показать, каким образом деформируются породы в процессе движения в них жидкости. Как следует из сказанного выше, эта деформация возникает в основном от двух причин: от изменения эффективных напряжений в породах в результате изменения давления жидкости на контакте кровля — пласт и от действия на породы градиентов давления фильтрующейся жидкости. Поясним более подробно, что это — разные причины. Эффективные напряжения в породах могут появиться в результате изменения величин в соотношении 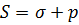как при наличии, так и при отсутствии движения жидкости. Градиенты давления действуют на горные породы только при наличии движения жидкости. Иногда деформация горных пород при движении в них жидкости может быть обусловлена только действием на породы градиентов давления фильтрующейся жидкости. Например, если фильтрация жидкости происходит из сферической полости в пласт очень большой мощности, не насыщенный жидкостью, движение можно «читать центрально-симметричным — тогда не может быть речи о деформации горных пород в результате изменения давления жидкости на контакте кровли и подошвы с пластом. Ведь кровля и подошва находятся очень далеко от сферической полости, а пласт первоначально даже не насыщен жидкостью. Деформация пород обусловлена только градиентами давления фильтрующейся жидкости.

Можно предложить мысленный эксперимент, в котором условно разделяются деформация пород, возникающая в результате действия градиентов давления фильтрующейся жидкости, и деформация пород в результате изменения эффективного напряжения на контакте кровли и подошвы с пластом. Так, если взять образец пористой среды длиной 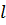(рис. 7.9), покрытый непроницаемой абсолютно гибкой оболочкой, и на конце его поддерживать давление жидкости 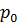, а при 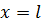давление жидкости равно нулю, то распределение давления жидкости 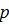будет

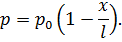(7.15)

Если снаружи к образцу приложить согласно рис. 7.3 полное напряжение

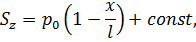(7.16)

то в соответствии с соотношением (7.2) предыдущего параграфа эффективное напряжение 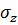будет постоянным, например, таким, каким оно было до фильтрации. Градиенты же давления жидкости будут действовать на пористую среду образца.

Из сказанного выше следует, что деформацию пород от действия эффективных напряжений, возникающих из-за появления контактных усилий на границе пласта с кровлей и подошвой, и деформацию от действия градиентов давления фильтрующейся жидкости нужно учитывать раздельно. Поэтому, в принципе, в каждом отдельном случае деформация горных пород по-разному влияет на процесс фильтрации жидкости.

В целом ряде практически важных случаев фильтрации в упругих пластах эффективное среднее нормальное напряжение 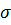, возникающее в результате действия на породы градиентов давления фильтрующейся жидкости, зависит от разности давления жидкости 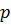и давления жидкости на контуре питания 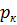следующим образом:

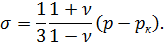(7.17)

На деформацию пласта при упругом режиме, естественно, оказывают большое влияние окружающие пласт породы. Если породы кровли и подошвы пласта более жесткие (имеют более высокое значение модуля Юнга), чем породы самого пласта, то они препятствуют деформации пород пласта, если же породы кровли и подошвы более гибкие> чем породы пласта, то они мало влияют на деформацию пласта. В последнем случае, если считать к тому же, что при действии на пласт контактных усилий каждый элемент пласта не деформируется в горизонтальном направлении вследствие «подпора» со стороны окружающих элементов, то и от действия контактных усилий в породах возникает точно такое же напряжение, какое определяется формулой (7.17). В этом случае суммарное эффективное напряжение, возникающее в породах при упругом режиме, будет выражаться формулой

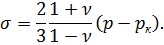(7.18)

При ,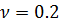

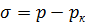при ,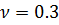

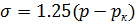при .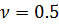

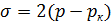Таким образом, иногда в теории упругого режима можно с известным приближением пользоваться коэффициентами сжимаемости пористой среды, полученными в лабораторных условиях, хотя, конечно, лучше определять сжимаемость на основе результатов натурных гидродинамических исследований.

На тех глубинах, где в настоящее время разрабатываются месторождения полезных ископаемых и, в частности, нефтяные и газовые месторождения, породы — коллекторы нефти и газа можно во многих практических случаях считать упругими. При переходе же на большие глубины, а также в тех случаях, когда давление насыщающей породу жидкости близко к горному давлению и, следовательно, сами породы в естественных условиях слабо нагружены, они будут большей частью деформироваться пластически, необратимо, а также будут проявлять свойства текучести.

В случае различной деформации пород при их нагружении и разгрузке движение жидкости в пластах будет происходить при упруго-пластическом режиме, теория которого была разработана Г. И. Баренблаттом и А. П. Крыловым. Для этого режима справедливы следующие уравнения: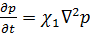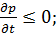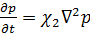

при при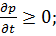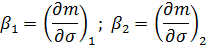

(7.19)

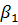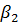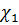где и , и 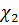– соответственно сжимаемость пород и пьезопроводность при нагружении пород и при разгрузке.

При упруго-пластическом режиме пластическая деформация самой породы в каждом элементарном объеме происходит мгновенно, т. е. текучести породы не наблюдается.

8 МЕХАНИЗМ ОБРАЗОВАНИЯ ТРЕЩИН В ГОРНЫХ ПОРОДАХ ПРИ ГИДРАВЛИЧЕСКОМ РАЗРЫВЕ ПЛАСТА\

В механизме распространения трещин в упругих материалах важное значение имеет условие конечности напряжений в концах трещины, известное как условие С. А. Христиановича. Для того чтобы лучше понять смысл этого условия, рассмотрим в качестве примера остроконечную трещину, образовавшуюся в бесконечной упругой плоскости под действием равномерной нагрузки 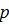, приложенной к внутренней поверхности трещины. Решение этой задачи, полученное методом Н. И. Мусхелишвили.

Не производя подробное вычисление всего поля напряжений, можно показать, что в концах такой трещины, т. е. при 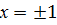, напряжения неограниченно возрастают. Например, напряжение 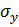на оси 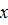определяется формулой

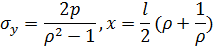(8.1)

Полагая 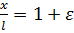( 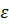— малая величина), из (8.1) получаем, что при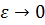

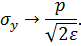		(8.2)

Таким образом, напряжение вблизи конца трещины безгранично возрастает. Поскольку ни один реальный материал не может выдержать бесконечно больших напряжений, трещина, находящаяся только под действием сил, стремящихся ее расширить, будет распространяться неограниченно.

Когда же на хрупкий материал, содержащий одну или несколько трещин, действуют две системы сил, одна из которых стремится расширить трещину, а другая — ее сомкнуть, то между размерами трещины и величиной действующих на материал сил может установиться строго определенное соотношение, причем напряжения в концах трещин не будут бесконечно большими, а поверхности трещин будут плавно смыкаться. Если материал с трещиной находится в описанном выше состоянии, это и означает, что в нем выполняется условие С. А. Христиановича.

Вместе с тем, если рассматривается деформация хрупкого материала от двух «противоположно направленных» систем постоянных сил, то для нахождения такого равновесного состояния, при котором размеры трещин не изменяются, достаточно из всех возможных решений соответствующей задачи выбрать такое, при котором напряжения на концах трещины будут конечными. Это будет означать, что найдено решение, при котором выполняется условие С. А. Христиановича.

Нужно сказать, что не при всяких противоположно направленных системах сил может существовать в материале равновесное состояние, при котором трещина будет иметь установившиеся конечные размеры. В одних случаях трещина может «выйти» за пределы материала, в котором она образуется, в других она окажется сомкнутой. Например, если на плоскость с трещиной действуют сжимающие силы 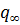, приложенные на бесконечно большом расстоянии от концов трещины, то условием конечности напряжений в концах трещины будет 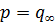. Однако трещина оказывается при этом сомкнутой, т. е. всюду на ее контуре смещение .

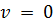Вертикальные трещины