Механический смысл компонент тензора деформаций

Выясним сначала механический смысл компоненты .

Рассмотрим малый отрезок, который до деформации был параллелен оси (рисунок 4.3). Обозначим через его длину до деформации, - длину после деформации. Имеем для этого отрезка

, .

Из (4.3) получаем

Рисунок 4.3 – Деформация малых отрезков, изначально параллельных координатным осям. Справа – отрезки до деформации, слева – отрезки после деформации

Введем понятия коэффициентов растяжения и относительного удлинения отрезков.

Коэффициент растяжения :

Коэффициент относительного удлинения :

Коэффициенты растяжения и относительного удлинения рассматриваемого отрезка равны соответственно

Кроме того,

Поделив обе части последнего равенства на , получим

Таким образом,

или

(4.4)

В случае малых деформаций , , поэтому с точностью до малых первого порядка

(4.5)

Вид соотношения (4.5) объясняет, для чего введен множитель 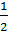в формулах (4.2), определяющих компоненты тензора деформаций. Без этого множителя в случае малых деформаций было бы , что представляется менее естественным.

Рассматривая отрезки, лежавшие до деформации параллельно осям или , получим формулы, аналогичные (4.4), (4.5). Итак,

то есть ( ) определяются относительными удлинениями отрезков, которые до деформации были параллельны соответственно координатным осям .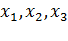

В случае малых деформаций , то есть ( ) равны относительным удлинениям отрезков, которые до деформации были параллельны соответственно осям .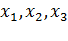

Выясним теперь механический смысл компонент тензора деформаций при . Из определения компонент следует, что:

(4.6)

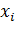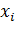где – соответственно коэффициенты растяжения и относительного удлинения отрезка, до деформации параллельного координатной оси , а – разность между первоначально прямым углом между отрезками, которые до деформации были параллельны соответственно осям и , и углом между этими отрезками после деформации (рисунок 4.4):

.

Рисунок 4.4 – Изменение угла между материальными отрезками при деформации

При малых деформациях и малы, поэтому с точностью до малых высшего порядка верны формулы

при .

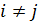(4.7)

Эти формулы используются в теории малых деформаций. Итак, в случае малых деформаций , , – это коэффициенты относительных удлинений отрезков, параллельных координатным осям, а 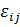при 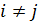равны половинам величин изменения углов между отрезками, которые до деформации были параллельны соответственно осям и . В простейшем двумерном случае малые деформации проиллюстрировать на примере квадрата.

Тело до деформации

Растяжение-сжатие

Сдвиг

Рисунок 4.5 – Геометрическая интерпретация тензора малых деформаций

Величина относительного изменения малого объема в случае малых деформаций определяется формулой:

(4.8)

где - первый инвариант тензора деформаций. В декартовых координатах

.

(4.9)