Численное дифференцирование и интегрирование в математическом моделировании, вычисление интегралов методом Симпсона и методом трапеций.
Задание:
1) Вычислить интеграл по формуле трапеций.
2) Вычислить интеграл по формуле Симпсона при n=8; оценить погрешность результата, составив таблицу конечных разностей.
Теоретическая часть
Метод трапеций
Если функцию на каждом из частичных отрезков аппроксимировать прямой, проходящей через конечные значения, то получим метод трапеций.
Площадь трапеции на каждом отрезке:
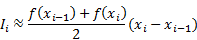
Погрешность аппроксимации на каждом отрезке:
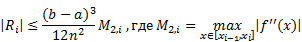
Полная формула трапеций в случае деления всего промежутка интегрирования на отрезки одинаковой длины 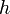 :
:
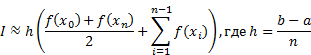
Погрешность формулы трапеций:
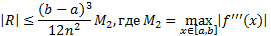
Метод парабол (метод Симпсона)
Использовав три точки отрезка интегрирования, можно заменить подынтегральную функцию параболой. Обычно в качестве таких точек используют концы отрезка и его среднюю точку. В этом случае формула имеет очень простой вид
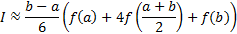
Если разбить интервал интегрирования на 2N равных частей, то имеем
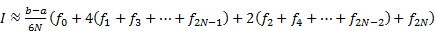 ,
,
где 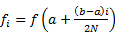
Увеличение точности
Приближение функции одним полиномом на всем отрезке интегрирования, как правило, приводит к большой ошибке в оценке значения интеграла.
Для уменьшения погрешности отрезок интегрирования разбивают на части и применяют численный метод для оценки интеграла на каждой из них.
При стремлении количества разбиений к бесконечности, оценка интеграла стремится к его истинному значению для аналитических функций для любого численного метода.
Приведённые выше методы допускают простую процедуру уменьшения шага в два раза, при этом на каждом шаге требуется вычислять значения функции только во вновь добавленных узлах. Для оценки погрешности вычислений используется правило Рунге.
Варианты заданий
№1. 1) 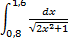 ; 2)
; 2) 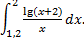
№2. 1) 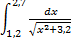 ; 2)
; 2) 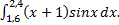
№3. 1) 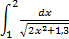 ; 2)
; 2) 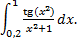
№4. 1) 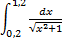 ; 2)
; 2) 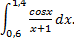
№5. 1) 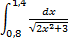 ; 2)
; 2) 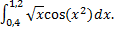
№6. 1) 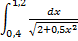 ; 2)
; 2) 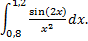
№7. 1) 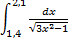 ; 2)
; 2) 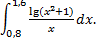
№8. 1) 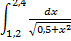 ; 2)
; 2) 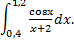
№9. 1) 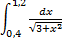 ; 2)
; 2) 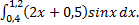
№10. 1) 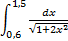 ; 2)
; 2) 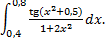
№11. 1) 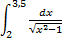 ; 2)
; 2) 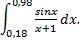
№12. 1) 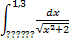 ; 2)
; 2) 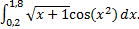
№13. 1) 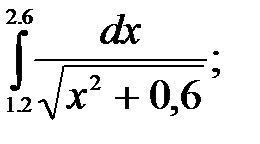 2)
2) 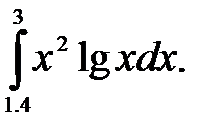
№14. 1)  2)
2) 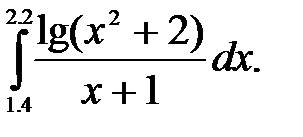
№15. 1) 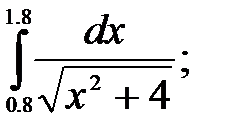 2)
2) 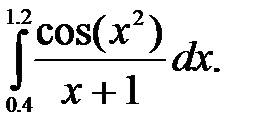
№16. 1) 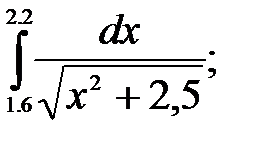 2)
2) 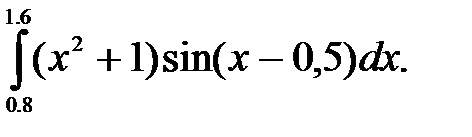
№17. 1) 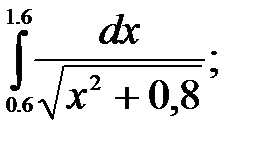 2)
2) 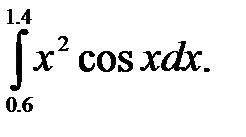
№18. 1) 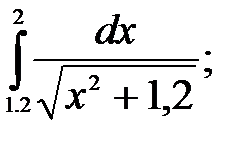 2)
2) 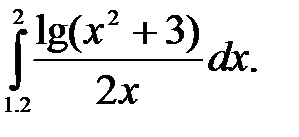
№19. 1) 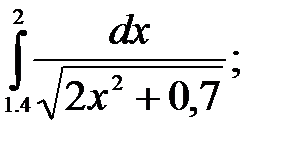 2)
2) 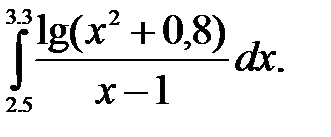
№20. 1) 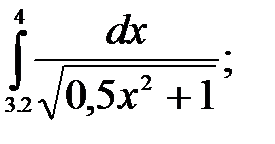 2)
2) 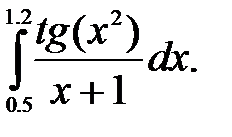
№21. 1) 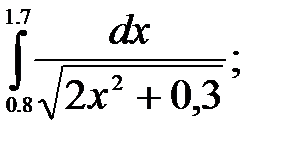 2)
2) 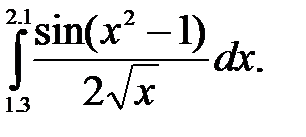
№22. 1) 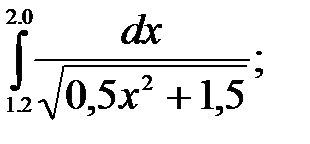 2)
2) 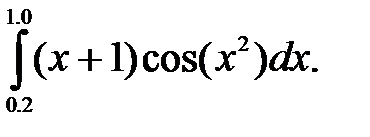
№23. 1) 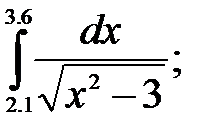 2)
2) 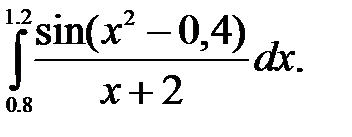
№24. 1) 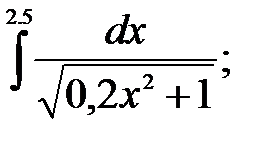 2)
2) 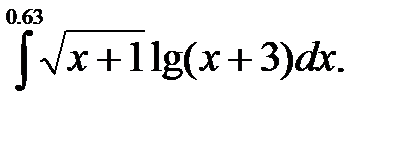
№25. 1) 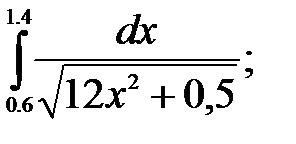 2)
2) 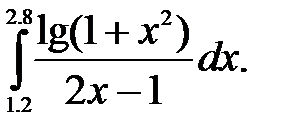
№26. 1) 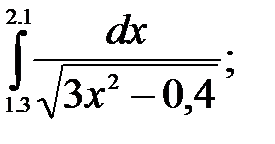 2)
2) 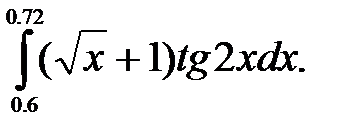
№27. 1) 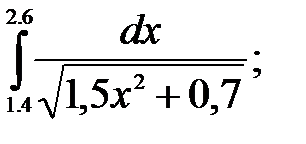 2)
2) 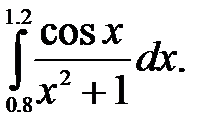
№28. 1) 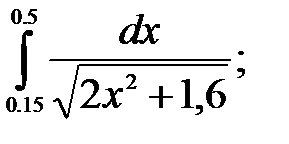 2)
2) 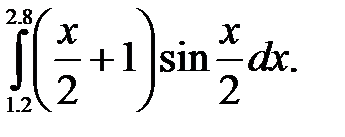
№29. 1) 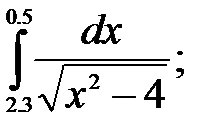 2)
2) 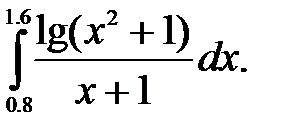
№30. 1) 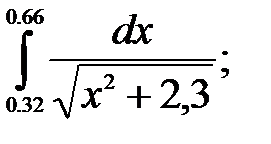 2)
2) 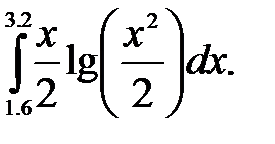
Образец выполнения задания
1) 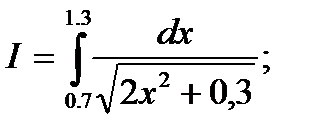 2)
2) 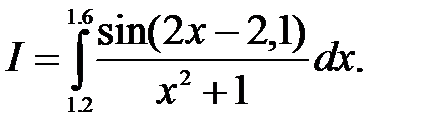
Задание №1. Решение методом трапеций
Для решения интегралов по методу трапеций необходимо определить значение nтак, чтобы
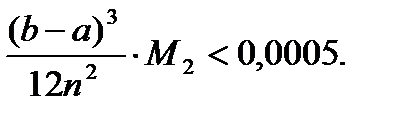 | (*) |
Здесь 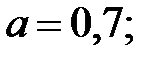
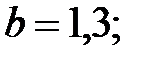
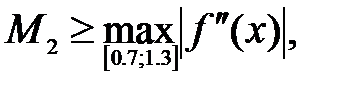 где
где 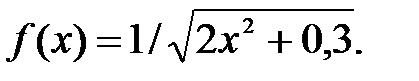
Находим
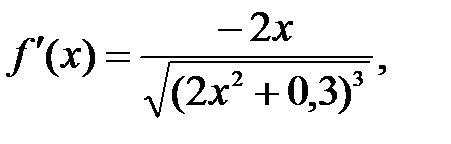
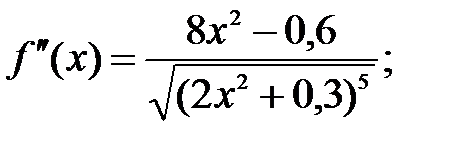
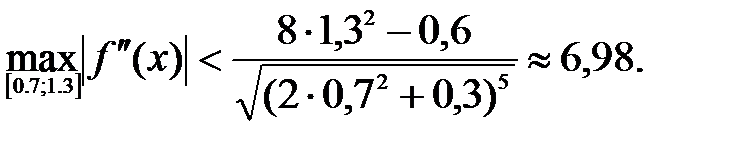
Положим 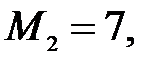 тогда неравенство (*) примет вид
тогда неравенство (*) примет вид 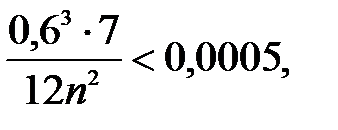 откуда
откуда 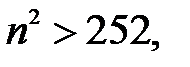 т.е.
т.е. 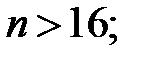 возьмем
возьмем 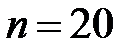 .
.
Вычисление интеграла производим по формуле
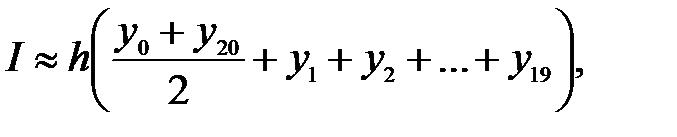
Где 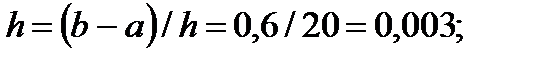
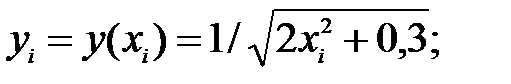
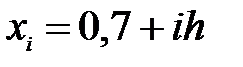
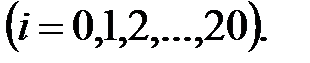
Все расчеты приведены в табл. 7.
Таблица 7
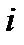 | 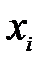 | 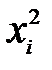 | 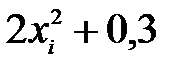 | 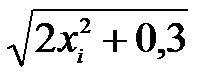 | 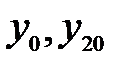 | 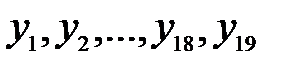 |
| 0,7 0,73 0,76 0,79 0,82 0,85 0,88 0,91 0,94 0,97 1,00 1,03 1,06 1,09 1,12 1,15 1,18 1,21 1,24 1,27 1,30 | 0,49 0,5329 0,5776 0,6241 0,6724 0,7225 0,7744 0,8281 0,8836 0,9409 1,0000 1,0609 1,1236 1,1881 1,2544 1,3225 1,3924 1,4641 1,5376 1,6129 1,6900 | 1,28 1,3658 1,4552 1,5482 1,6448 1,7450 1,8488 1,9562 2,0672 2,1818 2,3000 2,4218 2,5472 2,6762 2,8088 2,9450 3,0848 3,2282 3,3752 3,5258 3,6800 | 1,1314 1,1686 1,2063 1,2443 1,2825 1,3210 1,3597 1,3986 1,4378 1,4771 1,5166 1,5562 1,5960 1,6356 1,6759 1,7161 1,7564 1,7967 1,8372 1,8777 1,9187 | 0,88386 0,52129 | 0,85572 0,82898 0,80366 0,77973 0,75700 0,73546 0,71501 0,69551 0,67700 0,65937 0,64259 0,62657 0,61140 0,59669 0,58272 0,56935 0,55658 0,54431 0,53253 | |
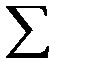 | 1,40515 | 12,77022 |
Таким образом,
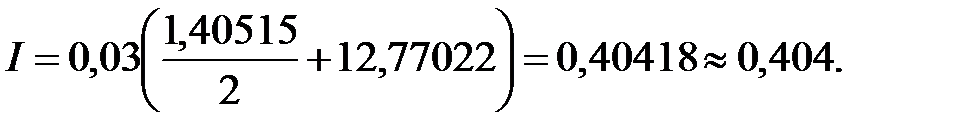
Задание № 2.Решение методом Симпсона
Согласно условию 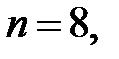 поэтому
поэтому 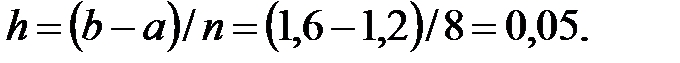
Вычислительная формула имеет вид
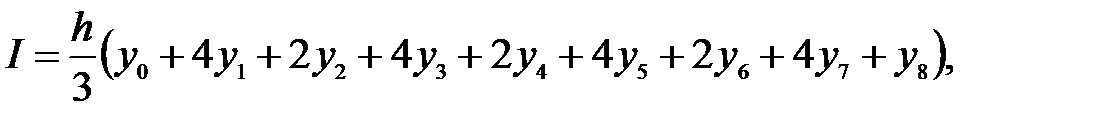
где 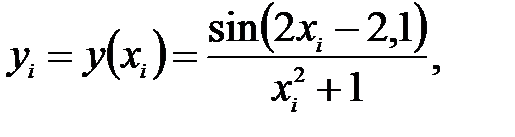
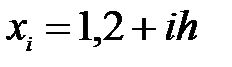
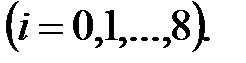
Вычисление значений функции, а также сложение значений функции, имеющих одинаковые коэффициенты в формуле, производим в табл.8.
Таблица8
| i | xi | 2xi-2,1 | sin(2xi-2,1) | xi2+1 | y0,y8 | y1,y3,y5,y7 | y2,y4,y6 |
| 1,20 | 0,30 | 0,29552 | 2,44 | 0,1211 | |||
| 1,25 | 0,40 | 0,38942 | 2,5625 | 0,1520 | |||
| 1,30 | 0,50 | 0,4794 | 2,69 | 0,1782 | |||
| 1,35 | 0,60 | 0,5646 | 2,8225 | 0,2000 | |||
| 1,40 | 0,70 | 0,6442 | 2,96 | 0,2176 | |||
| 1,45 | 0,80 | 0,7174 | 3,1024 | 0,2312 | |||
| 1,50 | 0,90 | 0,7833 | 3,25 | 0,2410 | |||
| 1,55 | 1,00 | 0,8415 | 3,4025 | 0,2473 | |||
| 1,60 | 1,10 | 0,8912 | 3,56 | 0,2503 | |||
| ∑ | 0,8305 | 0,6368 |
Следовательно,
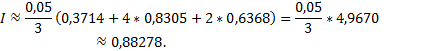
Для оценки точности полученного результата составим таблицу конечных разностей функций до разностей четвертого порядка (табл. 9).
Таблица 9
| i | yi | ∆yi | ∆2yi | ∆3yi | ∆4yi |
| 0,1211 0,1520 0,1782 0,2000 0,2176 0,2312 0,2410 0,2473 0,2503 | 0,0309 0,0262 0,0218 0,0176 0,0136 0,0098 0,0063 0,0030 | -0,0047 -0,0044 -0,0042 -0,0040 -0,0038 -0,0035 -0,0033 | 0,0003 0,0002 0,0002 0,0002 0,0003 0,0002 | -0,0001 0,0000 0,0000 0,0001 -0,0001 |
Так как 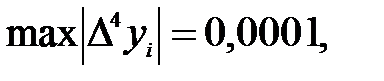 то остаточный член формулы
то остаточный член формулы 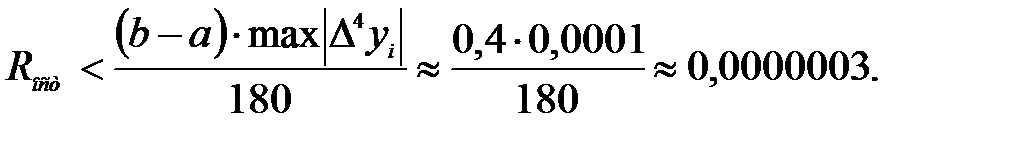
Вычисления производились с четырьмя значащими цифрами, а потому величина остаточного члена на погрешность не влияет.
Погрешность вычислений можно оценить из соотношения
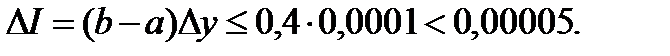
Значит, полученные четыре десятичных знака верны.
Контрольные вопросы
1) Способ уменьшения погрешности нахождения интеграла в методе прямоугольников и трапеций.
2) Объяснить какой аппроксимирующей функцией в методе Симпсона заменяется подынтегральная функция.
3) Обязательно ли участок интегрирования разбивать при реализации метода на более мелкие участки.
4) Объяснить, какие изменения произойдут в алгоритме, если для построения аппроксимирующей функции средняя точка берется не в середине участка.
5) Назвать случаи использования автоматического подбора шага интегрирования.
6) Объяснить изменение погрешности нахождения интеграла при уменьшении числа разбиений n.
Лабораторная работа № 5.
