Вопрос 1. нагрузки и напряжения в деталях машин

ВОПРОС 1. НАГРУЗКИ И НАПРЯЖЕНИЯ В ДЕТАЛЯХ МАШИН

В конструкциях детали работают в различных условиях, которые в совокупности образуют режимы нагружения – закономерности изменения нагрузки в конкретных условиях внешней среды. При этом, под нагрузкой понимают не только механическое воздействие (сила, момент), но и любое другое действие, например тепловое, вызывающее деформацию деталей.

По характеру нагружения внешние силы разделяют на поверхностные, и объемные, сосредоточенные и распределенные.

По характеру изменения нагрузки во времени их подразделяют на статические и циклические.

Статические нагрузки – не изменяющиеся или медленно изменяющиеся во времени.

Циклические нагрузки – нагрузка изменяющаяся во времени.

Циклические нагрузки характеризуются параметрами цикла:

- амплитудой напряжений σ_а;

- средним напряжением σ_m,;

- коэффициентом ассиметрии цикла r;

Циклическая нагрузка и соответственно напряжения представляются некоторой беспорядочной кривой, в которой, однако, можно установить определенную закономерность

Схематизированная картина напряжений представляется следующими синусоидальными циклами:

- асимметричный цикл

Среднее напряжение цикла – ;

Амплитудное напряжение цикла – ;

Коэффициент асимметрии цикла – .

- пульсирующий цикл:

Среднее напряжение цикла – ;

Минимальное напряжение – ;

Максимальное напряжение – ;

Коэффициент асимметрии цикла – .

- знакопеременный цикл:

Среднее напряжение цикла – ;

Амплитудное напряжение цикла – ;

Коэффициент асимметрии цикла – .

В зависимости от числа циклов нагружения само нагружение бывает статическим, малоцикловым и многоцикловым.

В соответствии с этим модели разрушения бывают:

- статическая модель разрушения – при действии кратковременных больших сил;

- малоцикловая – 10²-10⁵ циклов;

- усталостная - при числе циклов нагружения более 10⁵.

ВОПРОС 5. КЛАССИФИКАЦИЯ СОЕДИНЕНИЙ. ТРЕБОВАНИЯ К СОЕДИНЕНИЯМ В МАШИНОСТРОЕНИИ.

Детали, составляющие машину, связаны между собой тем или иным способом. Эти связи можно разделить на подвижные (различного рода шарниры, подшипники, зацепления и пр.) и неподвижные (резьбовые, сварные, шпоночные и др.). Наличие подвижных связей в машине обусловлено ее кинематической схемой. Неподвижные связи обусловлены целесообразностью расчленения машины на узлы и детали для того, чтобы упростить производство, облегчить сборку, ремонт, транспортировку и т. п.

Неподвижные связи в технике называют соединениями.

По признаку разъемности все виды соединений можно разделить на разъемные и неразъемные.

Разъемные соединения позволяют разъединять детали без их повреждения. К ним относятся резьбовые, штифтовые, клеммовые, шпоночные, шлицевые и профильные соединения.

Неразъемные соединения не позволяют разъединять детали без их повреждения. Применение неразъемных соединений обусловлено в основном технологическими и экономическими требованиями. К этой группе соединений относятся заклепочные, сварные и соединения с натягом.

Соединения с натягом отнесены к группе неразъемных условно, так как они позволяют производить повторную сборку и разборку, при этом происходит частичное повреждение сопрягаемых поверхностей, приводящее к уменьшению нагрузочной способности соединений.

Основным критерием работоспособности и расчета соединений является прочность.

Необходимо стремиться к тому, чтобы соединение было равнопрочным с соединяемыми элементами. Наличие соединения, которое обладает прочностью, составляющей, например, 0,8 от прочности самих деталей, свидетельствует о том, что 20% нагрузочной способности этих деталей или соответствующая часть металла конструкции не используется.

Желательно, чтобы соединение не искажало форму изделия, не вносило дополнительных элементов в его конструкцию и т. п. Например, соединение труб болтами требует образования фланцев, сверления отверстий под болты, установку самих болтов с гайками и шайбами. Соединение труб сваркой встык не требует никаких дополнительных элементов. Оно в наибольшей степени приближает составное изделие к целому. С этих позиций соединение болтами может быть оправдано только разъемностью.

Расчёт резьбы на прочность.

Основные виды разрушения резьб:

крепежных — срез витков,

ходовых — износ витков.

В соответствии с этим основными критериями работоспособности и расчета для крепежных резьб являются прочность, связанная с напряжениями среза , а для ходовых резьб ‑ износостойкость, связанная с напряжениями смятия

Условия прочности резьбы по напряжениям среза:

для винта

для гайки

где Н ‑ высота гайки или глубина завинчивания винта в деталь;

или ‑ коэффициент полноты резьбы;

‑ коэффициент неравномерности нагрузки по виткам резьбы.

Если материалы винта и гайки одинаковы, то по напряжениям среза рассчитывают только резьбу винта, так как d₁ < d.

Условие износостойкости ходовой резьбы по напряжениям смятия:

где ‑ число рабочих витков (например, число витков гайки).

ВОПРОС 14. РАСЧЁТ НА ПРОЧНОСТЬ БОЛТА ПРИ РАЗЛИЧНЫХ СЛУЧАЯХ НАГРУЖЕНИЯ (БОЛТ НАГРУЖЕН СИЛОЙ СДВИГАЮЩЕЙ ДЕТАЛИ И ПОСТАВЛЕН С ЗАЗОРОМ И БЕЗ ЗАЗОРА)

Условием надежности соединения является отсутствие сдвига деталей в стыке. Конструкция может быть выполнена в двух вариантах:

Болт поставлен с зазором. При этом внешнюю нагрузку F уравновешивают силы трения в стыке, которые образуются от затяжки болта. Без затяжки болтов детали могут сдвигаться в пределах зазора, что недопустимо.

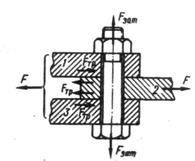
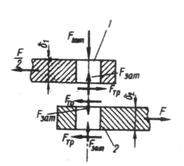
Рассматривая равновесие детали 2, получим условие отсутствия сдвига деталей:

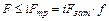
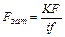
где i ‑ число плоскостей стыка деталей; при соединении только двух деталей i=1;

f ‑ коэффициент трения в стыке (f = 0,15...0,20 для сухих чугунных и стальных поверхностей);

К ‑ коэффициент запаса (K = 1,3…1,5 при статической нагрузке; К = 1,8…2 при переменной нагрузке).

Прочность болта оценивают по эквивалентному напряжению.

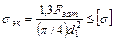
Отметим, что в соединении, в котором болт поставлен с зазором, внешняя нагрузка не передается на болт. Поэтому болт рассчитывают только на статическую прочность по силе затяжки даже при переменной внешней нагрузке. Влияние переменной нагрузки учитывают путем выбора повышенных величин коэффициента запаса.

Болт поставлен без зазора. Такая установка болта в отверстие соединяемых деталей обеспечивает восприятие внешней нагрузки стержнем болта. При расчете прочности соединения не учитывают силы трения в стыке, так как затяжка болта в принципе не обязательна. В общем случае болт можно заменить штифтом. Стержень болта рассчитывают по напряжениям среза и смятия.

Условие прочности по напряжениям среза:

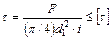
где i ‑ число плоскостей среза.

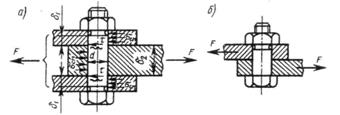
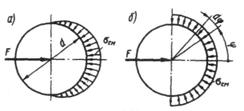
Условие прочности по напряжениям смятия:

для средней детали

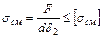
для крайней детали

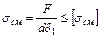
Эти формулы справедливы для болта и деталей. Из двух величин напряжений 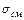в этих формулах расчет прочности выполняют по наибольшей, а допускаемое напряжение определяют по более слабому материалу болта или детали.

Способы сборки

Сборку соединения выполняют одним из трех способов: прессованием, нагревом втулки, охлаждением вала.

Прессование — распространенный и несложный способ сборки. Однако этому способу свойственны недостатки: смятие и частичное срезание (шабровка) шероховатостей посадочных поверхностей, возможность неравномерных деформаций деталей и повреждения их торцов. Шабровка и смятие шероховатостей приводят к ослаблению прочности соединения до полутора раз по сравнению со сборкой нагревом или охлаждением. Для облегчения сборки и уменьшения шабровки концу вала и краю отверстия рекомендуют придавать коническую форму (рис. 7.2).

Шабровка поверхностей контакта устраняется полностью при сборке по методу нагревания втулки (до 200…400°С) или охлаждения вала (твердая углекислота -79°С, жидкий воздух -196°С). Недостатком метода нагревания является возможность изменения структуры металла появление окалины и коробления. Метод охлаждения свободен от этих недостатков.

Шпонки тангенциальные

Поперечное сечение прямоугольник. В поперечном сечении соединения шпонка одной своей широкой стороной располагается касательно к окружности вала ‑ втулки. Шпонка состоит из двух односкосных одинакового уклона клиньев, составленных таким образом, что узкие грани ‑ они являются рабочими ‑ параллельны. Эти шпонки применяются сравнительно редко.

Прочность узкой грани по смятию проверяется по условию

где - ширина фаски;

Сегментная шпонкаявляется разновидностью призматической шпонки, так как принцип работы этой шпонок подобен принципу работы призматической шпонки. Основные размеры сегментных шпонок b×h×D (ширина, высота, диаметр заготовки) стандартизованы в зависимости от диаметра вала ГОСТ 24071-80. Длина шпонки l.

Аналогично соединению с призматической шпонкой для сегментной шпонки получим

При длинных ступицах можно ставить в ряд по оси вала две сегментные шпонки.

Соединения с цилиндрической шпонкой

Цилиндрическую шпонку используют для закрепления деталей на конце вала. Цилиндрическую шпонку устанавливают в отверстие с натягом. В некоторых случаях шпонке придают коническую форму.

Условие прочности соединения цилиндрической шпонкой по напряжениям смятия:

Расчет зубчатых соединений

Основными критериями работоспособности и расчета зубчатых соединений являются:

- сопротивление рабочих поверхностей смятию;

-- сопротивление изнашиванию от фреттинг-коррозии (это коррозионно-механическое изнашивание при малых относительных колебательных перемещениях соприкасающихся поверхностей).

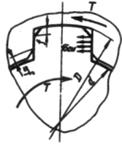
Упрощенный расчет по обобщенному критерию. Вупрощенной расчетной модели принято равномерное распределение нагрузки по длине зубьев. При этом получают:

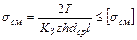
где 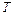‑ номинальный крутящий момент (наибольший из длительно действующих);

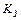= 0,7…0,8 ‑ коэффициент неравномерности нагрузки по зубьям;

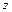‑ число зубьев;

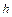‑ рабочая высота зубьев;

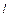‑ рабочая длина зубьев;

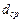‑ средний диаметр соединения.

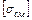- допускаемое напряжение смятия зависящее от типа соединения, условий эксплуатации и твёрдости зубьев.

Для прямобочных зубьев: ; .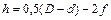

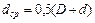для эвольвентных зубьев: ; .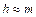

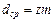где 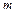‑ модуль зубьев;

Паяные соединения

Соединение образуется в результате химических связей материала деталей и присадочного материала, называемого припоем. Температура плавления припоя (например, олова) ниже температуры плавления материала деталей, поэтому в процессе пайки детали остаются твердыми. Размер зазора в стыке деталей в значительной мере определяет прочность соединения. Уменьшение зазора до некоторого предела увеличивает прочность. Размер оптимального зазора зависит от типа припоя и материала деталей. Для пайки стальных деталей тугоплавкими припоями (серебряными и медными) приближенно рекомендуют зазор 0,03…0,15 мм, при легкоплавких припоях (оловянных) ‑ 0,05…0,2 мм.

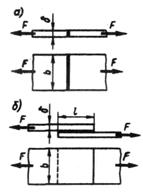Расчет прочности паяных соединений аналогичен расчету сварных.

Например, для стыковых соединений

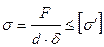
для нахлесточных соединений (рис. 4.4, 6)

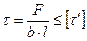
где 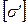и 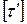‑ допускаемые напряжения в паяном шве.

Аналогично можно записать расчетные напряжения для других конструкций соединений.

Конструкция клеевых соединений подобна конструкции паяных, только припой здесь заменен клеем, а образование соединения выполняют без нагрева деталей. Соединение осуществляется за счет сил адгезии (сил сцепления) в процессе затвердевания жидкого клея.

Прочность клеевого соединения в значительной степени зависит от толщины слоя клея. Рекомендуемые значения 0,05...0,15 мм. Клеевые соединения лучше работают на сдвиг, хуже на отрыв. Поэтому предпочтительны нахлесточные соединения.

Расчеты на прочность производят по тем же формулам, что и для паяных соединений. Качество клеевого соединения характеризуется не только его прочностью, но также водостойкостью, теплостойкостью и другими показателями.

Заклёпочные соединения

Образуются с помощью специальных деталей – заклёпок. Заклёпка имеет грибообразную форму и выпускается с одной головкой (закладной) вставляется в совместно просверленные детали, а затем хвостовик ударами молотка или пресса расклёпывается, образуя вторую головку (замыкающую). При этом детали сильно сжимаются, образуя прочное, неподвижное неразъёмное соединение.

Достоинства заклёпочного соединения:

+ соединяют не свариваемые детали;

+ не дают температурных деформаций;

+ детали при разборке не разрушаются.

Недостатки заклёпочного соединения:

` детали ослаблены отверстиями;

` высокий шум и ударные нагрузки при изготовлении;

` повышенный расход материала.

Заклёпки изготавливают из сравнительно мягких материалов: Ст2, Ст3, Ст10, Ст15, латунь, медь, алюминий.

Заклёпки стандартизованы и выпускаются в разных модификациях.

‑ Сплошные с полукруглой головкой (а) ГОСТ 10299-80, 14797-85 для силовых и плотных швов;

‑ Сплошные с плоской головкой (б) ГОСТ 14801-85 для коррозионных сред;

‑ Сплошные с потайной головкой (в) ГОСТ 10300-80, 14798-85 для уменьшения аэро- и гидросопротивления (самолёты, катера);

‑ Полупустотелые (г,д,е) ГОСТ 12641-80, 12643-80 и пустотелые (ж,з,и) ГОСТ 12638-80, 12640-80 для соединения тонких листов и неметаллических деталей без больших нагрузок.

Заклёпки испытывают сдвиг (срез) и смятие боковых поверхностей. По этим двум критериям рассчитывается диаметр назначаемой заклёпки. При этом расчёт на срез – проектировочный, а расчёт на смятие – проверочный.

Здесь и далее имеем в виду силу, приходящуюся на одну заклёпку.

При одной плоскости среза диаметр заклёпки:	При двух плоскостях среза (накладки с двух сторон):

Напряжения смятия на боковых поверхностях заклёпки s_см =P/Sd ≤[s]_см,

где S – толщина наименьшей из соединяемых деталей. При проектировании заклёпочных швов как, например, в цистернах, необходимо следить, чтобы равнодействующая нагрузок приходилась на центр тяжести шва.

Расчетная нагрузка

За расчетную нагрузку принимают максимальную величину удельной нагрузки, распределенной по линии контакта зубьев:

где 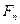‑ нормальная сила в зацеплении;

‑ коэффициент расчетной нагрузки;

‑ коэффициент распределения нагрузки между зубьями;

‑ коэффициент концентрации нагрузки;

‑ коэффициент динамической нагрузки;

‑ суммарная длина линии контакта зубьев.

Коэффициент распределения нагрузки между зубьями

Определяется в зависимости от степени точности ( ) изготовления зубчатых колес по нормам плавности. Он учитывает влияние ошибок окружного шага и направления зубьев на величину в ненагруженной передаче.

Коэффициент концентрации нагрузки

Концентрация или неравномерность распределения нагрузки по длине зуба связана с деформацией валов, корпусов, опор и самих зубчатых колес, а также с погрешностями изготовления и сборки передачи.

Коэффициент динамической нагрузки

Коэффициентом , учитывают только так называемые внутренние динамические нагрузки, присущие самой зубчатой передаче.

Геометрические параметры

Аналогами начальных и делительных цилиндров цилиндрических передач в конических передачах являются делительные конусы с углами и .

Конусы, образующие которых перпендикулярны образующим делительных конусов, называют дополнительными конусами.

Сечение зубьев дополнительным конусом называют торцовым сечением. Различают внешнее, внутреннее и среднее торцовые сечения. Размеры, относящиеся к внешнему торцовому сечению, сопровождают индексом . Размеры в среднем сечении сопровождают индексом т.

. и ‑ внешнее и среднее конусные расстояния,

‑ ширина зубчатого венца.

Размеры по внешнему торцу удобнее для измерения, их указывают на чертежах. Размеры в среднем сечении используют при силовых расчетах. Зависимости размеров в среднем и торцовом сечениях:

; ;

Для прямозубых передач торцовое t и нормальное п сечения совпадают. При этом = округляют до стандартного.

Передаточное числокак и у цилиндрических передач,

Кроме того, выразив и через конусное расстояние R и углы делительных конусов и , получим:

, и при ‑

Геометрические параметры

‑ угол профиля (в осевом сечении для архимедовых червяков и в нормальном сечении зуба рейки, сопряженной с витками эвольвентного червяка);

‑ осевой модуль. Резьба червяка может быть однозаходной или многозаходной. Число заходов червяка обозначают .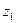

По стандарту, 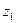= l; 2; 4. Рекомендуют: 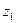= 4 при передаточном отношении i = 8…15; 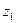= 2 при i = 15…30; 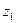= l при i > 30.

‑ коэффициент диаметра червяка.

Величины т и q стандартизованы. Для каждого модуля предусмотрены червячные фрезы при всех указанных q и .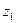

Для того чтобы исключить слишком тонкие червяки, стандарт предусматривает увеличение q с уменьшением т. При тонком червяке увеличивается прогиб червячного вала, что нарушает правильность зацепления. Рекомендуют .

Угол подъема винтовой линии .

Диаметры:

, ,

Длину нарезанной части червяка определяют в зависимости от числа заходов червяка 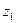и коэффициента смещения x.

Червячные колеса.

При нарезании без смещения диаметры колёс:

, ,

Межосевое расстояние передачи:

По условию неподрезания зубьев

Для нарезания червячных колес со смещением и без смещения на практике используют один и тот же инструмент. Поэтому червяк всегда нарезают без смещения. Смещение инструмента при нарезании колеса выполняют в целях получения передачи с заданным или стандартным межосевым расстоянием.

При заданном межосевом расстоянии a_w коэффициент смещения:

или

У червячного колеса со смещением:

,

все другие размеры остаются неизменными.

По условию неподрезания и незаострения зубьев величину х на практике рекомендуют изменять в пределах до ±0,7 (реже ± 1).

ВОПРОС 34. КИНЕМАТИЧЕСКИЕ ПАРАМЕТРЫ ЧЕРВЯЧНЫХ ПЕРЕДАЧ. (ПЕРЕДАТОЧНОЕ ОТНОШЕНИЕ И СКОРОСТЬ СКОЛЬЖЕНИЯ). СИЛЫ В ЗАЦЕПЛЕНИИ ЧЕРВЯЧНОЙ ПЕРЕДАЧИ.

Кинематические параметры передач

Передаточное отношение. Вчервячной передаче в отличие от зубчатой окружные скорости v₁ и v₂ направлены под углом 90° друг к другу и различны по величине. Поэтому червячная передача имеет следующие особенности: передаточное отношение не может быть выражено отношением . При одном обороте червяка колесо повернется на угол, охватывающий число зубьев колеса, равное числу заходов червяка. Для полного оборота колеса необходимо оборотов червяка, т. е.

Так как 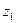может быть небольшим и часто равным единице (чего не может быть у шестерни), то в одной червячной паре можно получить большое передаточное отношение. Это и является основным достоинством червячных передач.

Скольжение в зацеплении. При движении витки червяка скользят по зубьям колеса, как в винтовой паре.Скорость скольжения направлена по касательной к винтовой линии червяка. Как относительная скорость она равна геометрической разности абсолютных скоростей червяка и колеса, которыми в данном случае являются окружные скорости и :

;

; ;

Здесь ‑ угол подъема винтовой линии червяка. Так как практически < 30°, то в червячной передаче всегда значительно меньше , a больше .

Большое скольжение в червячных передачах служит причиной пониженного КПД, повышенного износа и склонности к заеданию (основные недостатки червячных передач).

Силы в зацеплении

Вчервячном зацеплении действуют:

- окружная сила червяка равная осевой силе колеса :

- окружная сила колеса равная осевой силе червяка :

- радиальная сила:

- нормальная сила:

ВОПРОС 37 ПЛАНЕТАРНЫЕ ПЕРЕДАЧИ. ПРИНЦИП ДЕЙСТВИЯ. ОПРЕДЕЛЕНИЕ ПЕРЕДАТОЧНОГО ОТНОШЕНИЯ.

Планетарными называют передачи, содержащие зубчатые колеса с перемещающимися осями. Передача состоит из центрального колеса а с наружными зубьями, центрального колеса b с внутренними зубьями, водила h и сателлитов g.

Движение может передаваться

При неподвижном колесе b: от а к h или от h к а;

При неподвижном водиле h:от а к b или от b к а.

При всех свободных звеньях одно движение можно раскладывать на два или два соединять в одно, например от b к а и h, от а и h к b и т. п. в этом случае передачу называют дифференциальной.

Достоинствами планетарной передачи являются:

- широкие кинематические возможности;

- компактность;

- малая масса

- внутреннее зацепление (g и b) обладает повышенной нагрузочной способностью, так как у него больше приведенный радиус кривизны в зацеплении

- возможность получать большие передаточные отношения (до тысячи и больше) без применения многоступенчатых передач;

- малая нагрузка на опоры, так как при симметричном расположении сателлитов силы в передаче взаимно уравновешиваются.

К недостаткам планетарных передач относятся повышенные требования к точности изготовления и монтажа.

Кинематика планетарных передач

При исследовании кинематики планетарных передач широко используют метод остановки водила — метод Виллиса.

Всей планетарной передаче мысленно сообщается вращение с частотой вращения водила, но в обратном направлении. При этом водило как бы затормаживается, а все другие звенья освобождаются. Получаем так называемый обращенный механизм, представляющий собой простую передачу, в которой движение передается от а к b через паразитные колеса g. Частоты вращения зубчатых колес обращенного механизма равны разности прежних частот вращения и частоты вращения водила.

Для обращенного механизма:

В нашем случае колесо b заторможено, а ‑ ведущее и h ‑ ведомое, при = 0получаем:

;

или

Частоту вращения сателлита определяют из равенства:

При заданных и определяют или ( )как частоту вращения сателлита относительно водила или относительно своей оси (используют при расчете подшипников).

ВОПРОС 38. СИЛЫ В ЗАЦЕПЛЕНИИ ПЛАНЕТАРНОЙ ПЕРЕДАЧИ. РАСЧЕТ НА ПРОЧНОСТЬ ПЛАНЕТАРНОЙ ПЕРЕДАЧИ.

Силы в зацеплении

По условиям равновесия сателлита:

и ,

где

Здесь ‑ число сателлитов;

‑ коэффициент, учитывающий неравномерность распределения нагрузки между сателлитами.

Радиальные и осевые силы при известной окружной силе определяют так же, как и в простых передачах.

Значение зависит от точности изготовления и числа сателлитов.

Расчет на прочность.

Для расчета прочности зубьев планетарных передач используют те же формулы, что и при расчете простых передач. Расчет выполняют для каждого зацепления;

- для наружного зацепления ‑ колеса а и g,

- для внутреннего ‑ колеса g и b.

Так как силы и модули в этих зацеплениях одинаковы, а внутреннее зацепление по своим свойствам прочнее наружного, то при одинаковых материалах достаточно рассчитывать только зацепление колес а и g.

При разных материалах расчет внутреннего зацепления выполняют с целью подбора материала колеса или как проверочный.

При расчете на изгиб используют формулу.

Для расчета по контактным напряжениям в расчётных формулах учитываются число сателлитов и коэффициент неравномерности распределения нагрузки между ними. Например, формулу для проектного расчёта относительно делительного диаметра при К_На = 1 получим в виде

При расчете пары а ‑ g по формуле полагают, что ‑ диаметр меньшего колеса пары, а и равно отношению чисел зубьев большего колеса к числу зубьев меньшего.

Для планетарных передач рекомендуют

Оценка передачи

Основное достоинство передачи Новикова ‑ повышенная нагрузочная способность по контактной прочности. При H 350 НВ она примерно в 1,5…1,7 раза больше, чем у аналогичной по размерам и материалу эвольвентной косозубой передачи.

Недостатки — повышенная чувствительность к изменению межосевого расстояния; сравнительно сложный исходный контур инструмента, некоторое снижение изломной прочности по сравнению с эвольвентным профилем.

Особенности зацепления

Профили зуба шестерни и колеса в передаче Новикова не эвольвентный, а круговой. Причём у шестерни профиль зуба выпуклый, с радиусом кривизны , а у колеса вогнутым, с , несколько большим, но близким к . Контактные напряжения в передаче значительно уменьшаются, так как контакт выпуклых эвольвентных профилей заменен контактом выпуклого и вогнутого профилей с малой разностью радиусов кривизны. Для сохранения непрерывности зацепления передачи Новикова выполняют косозубыми с .

Если линия зацепления располагается за полюсной линией (по направлению вращения ведущего колеса), то зацепление называют заполюсным, если до полюса ‑ дополюсным. Одна и та же пара колес может иметь заполюсное или дополюсное зацепление в зависимости от того, какое из них является ведущим.

Признаком заполюсного зацепления является выпуклый профиль, у ведущего зуба и вогнутый у ведомого; дополюсного ‑ вогнутый у ведущего и выпуклый у ведомого. Очевидно, можно выполнить зубья так, чтобы одна часть их профиля была выпуклой, а другая ‑ вогнутой. Тогда они смогут зацепляться и за полюсом, и до полюса. Так был разработан вариант дозаполюсного зацепления.

Дозаполюсное зацепление имеет две линии зацепления, проводящие через точки а и б. Соответственно в два раза увеличивается и число точек контакта зубьев. В таких передачах зубья шестерни и колеса имеют одинаковый профиль: выпуклый ‑ у головки, вогнутый ‑ у ножки.

Принцип действия

Наружный диаметр недеформированного гибкого колеса меньше внутреннего диаметра жесткого колеса:

В передаче по варианту I с ведомым валом соединено жесткое колесо, по варианту II ‑ гибкое колесо. В варианте I левый недеформированный конец гибкого цилиндра присоединен к корпусу. С правого конца в цилиндр вставлен генератор, который в данном примере представлен водилом с двумя роликами.

Наружный размер по роликам больше внутреннего д