Графическое решение уравнений и систем уравнений
Цель работы: Ознакомиться с графическими методами решения уравнений и систем уравнений.
Основные теоретические положения.Кроме аналитического способа решения уравнений f(x) = 0 можно пользоваться и графическим способом. Графический способ наиболее эффективен для решения трансцендентных уравнений. При графическом способе для уравнения строится график y = f(x) и решением уравнения является точка пересечения графика с осью х при у = 0. Если разбить уравнение на две произвольные части, то можно для каждой части построить график. В этом случае решением уравнения будет абсцисса точки пересечения графиков для этих частей. Такой способ может использоваться и для решения систем двух линейных уравнений с двумя неизвестными.
Порядок выполнения работы
Задание 1. Решить графически уравнение y = cos2(px) на интервале [0; 1].
Задание 2. Решить графически уравнение х3 – 4х2 – 3х + 6 = 0.
Задание 3. Решить графически систему уравнений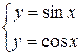 
в диапазоне хÎ[0; 3] с шагом Dх = 0,2.
Задание 4. Решить систему уравнений согласно индивидуальному заданию.
12.1. Выполнение задания 1
Решить графически уравнение y=cos2(px) на интервале [0;1] значит найти все значения х внутри данного интервала, где функция у пересекает ось Х.
12.1.1.Провести табуляцию значений х и у (см. Работу 11).
В результате получим табл. 9.
Таблица 9
| A | B | C | |
| График функции y=cos(Pi*x)^2 | |||
| Значение х | Значение у | Значение Pi | |
| = COS(A3*C$3)^2 | 3,1415 | ||
| 0,1 | = COS(A4*C$3)^2 | ||
| 0,2 | = COS(A5*C$3)^2 | ||
| 0,3 | = COS(A6*C$3)^2 | ||
| 0,4 | = COS(A7*C$3)^2 | ||
| 0,5 | = COS(A8*C$3)^2 | ||
| 0,6 | = COS(A9*C$3)^2 | ||
| 0,7 | = COS(A10*C$3)^2 | ||
| 0,8 | = COS(A11*C$3)^2 | ||
| 0,9 | = COS(A12*C$3)^2 | ||
| = COS(A13*C$3)^2 |
12.1.2. Построение графика функции (см. Работу 11).
В результате получим график (рис. 31). Из графика видно, что уравнение имеет единственный корень. Что-бы получить точное решение уравнения, нужно щелкнуть левой клавишей мыши по точке пересечения графика с осью ОХ. На графике появится текст (рис. 32).
Здесь Точка “0,5” – значение х
Значение “4,633Е-05”»0 – значение у.
12.2. Выполнение задания 2
Найдем графическое решение уравнения х3-4х2-3х+6=0.
Для этого представим его в виде
х3 = 4х2 + 3х – 6 (2)
и построим на одной диаграмме графики двух функций:
у1 = х3 левая часть уравнения (2) и
у2 = 4х2 + 3х – 6 правая часть уравнения (2)
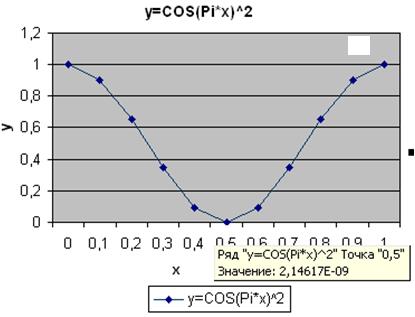
Рис. 32. График функции y=cos2(px)
Так как мы ищем корни кубического уравнения, число корней должно быть равно трем. Заранее значения корней неизвестны, поэтому сначала возьмем для построения графиков интервал хÎ[–2; 2], с шагом 0,4 и построим на этом интервале графики функций у1 и у2. Координаты точек х пересечения этих графиков дадут нам искомые значения корней.
Очевидно, что если корней должно быть три, то точек пересечения функций у1 и у2 тоже будет три. Если точек пересечения окажется меньше, нужно увеличить рассматриваемый интервал (например, построить график на интервале хÎ[–3; 3]).
12.2.1. Открыть новый рабочий лист (Щелчок правой клавишей по имени имеющегося листа – Добавить – Лист).
12.2.2. Провести табуляцию значений аргумента х и функций у1 и у2 (см. Работу 11). В результате получим табл. 10.
12.2.3. Строим график функций у1 и у1 на одной диаграмме (рис. 33). Из графиков видно, что на рассмотренном ин-тервале функции у1 и у2 пересекаются только два раза (корни х1 = –1,2 и х2 = 1,2).
Таблица 10
| A | B | C | |
| Решение уравнения x^3-4*x^2-3*x+6 | |||
| х | у1=х^3 | y2=4*x^2+3*x-6 | |
| -2 | =A3^3 | =4*A3^2+3*A3-6 | |
| -1,6 | =A4^3 | =4*A4^2+3*A4-6 | |
| -1,2 | =A5^3 | =4*A5^2+3*A5-6 | |
| -0,8 | =A6^3 | =4*A6^2+3*A6-6 | |
| -0,4 | =A7^3 | =4*A7^2+3*A7-6 | |
| =A8^3 | =4*A8^2+3*A8-6 | ||
| 0,4 | =A9^3 | =4*A9^2+3*A9-6 | |
| 0,8 | =A10^3 | =4*A10^2+3*A10-6 | |
| 1,2 | =A11^3 | =4*A11^2+3*A11-6 | |
| 1,6 | =A12^3 | =4*A12^2+3*A12-6 | |
| =A13^3 | =4*A13^2+3*A13-6 |
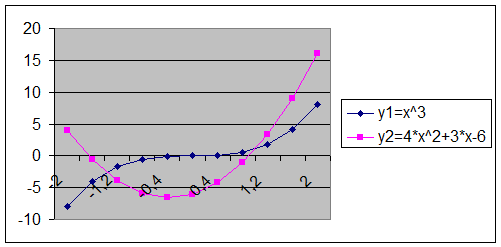
Рис. 33. Решение уравнения х3-4х2-3х+6=0.
12.2.3. Для нахождения третьего корня нужно увеличить диапазон решения. Из графика видно, что при х<–2 функции у1 и у2 расходятся.
Значит, решение нужно искать при х>2. Увеличим диапазон до х = 4,8, т. е. хÎ[–2; 4,8]:
а) продолжить табулирование аргумента х до ячейки А20;
б) скопировать формулу из ячейки В13 в ячейки В14:В20;
в) скопировать формулу из ячейки С13 в ячейки С14:С20;
г) построить график для этого случая. На этом графике функции у1 и у2 пересекаются трижды. Третий корень х3 = 4,4.
12.3. Выполнение задания 3
Решить графически систему уравнений значит найти координаты точек, в которых пересекаются графики функций, входящих в систему уравнений.
При выполнении задания 2 мы решили практически систему уравнений
.
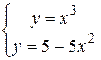Для нахождения корней уравнений системы
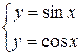
в диапазоне хÎ[0; 3] с шагом Dх = 0,2, следует выполнить следующие действия.
12.3.1. Добавить новый рабочий лист
12.3.2. Провести табулирование переменных х, y = sin x, y = cos x, аналогично Работе 11 и пп. 12.1, 12.2 данной работы:
- в ячейку А1 ввести заголовок Аргумент х, в ячейку А2 – значение 0, в ячейку А3 - значение 0,2 и провести табуляцию аргумента х в ячейках А2:А17;
- в ячейку В1 ввести заголовок y = sin(x);
- в ячейку В2 ввести формулу =SIN(A2) и скопировать ее в ячейки В3:В17;
- в ячейку С1 ввести заголовок y = cos(x);
- в ячейку С2 ввести формулу =COS(A2) и скопировать ее в ячейки C3:C17.
12.2.3. Построить график функций y = sin x, y = cos x на одной диаграмме:
а) выполнить команды Вставка – Диаграмма (Вставка – График);
б) в первом диалоговом окне Мастера диаграмм выберем Тип диаграммы График, Вид - Левый верхний, Далее;
в) во втором окне Мастера диаграмм на вкладке Диапазон данных ввести:
Диапазон В2:С17
Ряды в: столбцах;
Затем щелкнуть по вкладке Ряд и ввести:
Подписи оси Х А2:А17 ;
Щелкнуть по кнопке Далее;
г) в третьем окне Мастера диаграмм ввести:
Название диаграммы Система
Ось Х Аргумент
Ось У Значения
щелкнуть по кнопке Далее;
д) на последнем шаге Мастера диаграмм выбрать опцию
На отдельном листеи щелкнуть Готово.
На полученном графике (рис. 34) видно, что в указанном диапазоне система имеет единственное решение (графики имеют только одну точку пересечения).
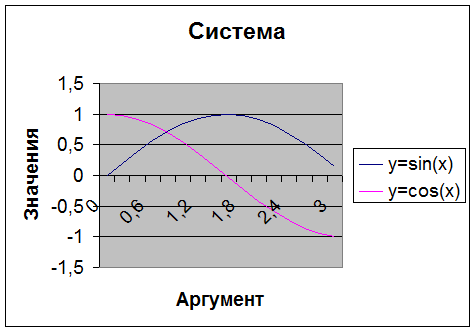
Рис. 34. Решение системы уравнений
Для нахождения решения:
- поставить указатель мыши в точку пересечения графиков;
- щелкнуть левой клавишей мыши. Появится надпись с указанием приблизительного решения системы уравнений:
Ряд “y=cos(x)” Точка “0,8”
Значение: 0,6967067
Следовательно, решением уравнения являются:
х = 0,8
у = 0,697.
12.4. Выполнение задания 4
12.4.1. Выбрать из табл. 11 индивидуальное задание по указанию преподавателя.
12.4.2. Добавить новый рабочий лист.
12.4.3. Графически решить систему уравнений в указанном диапазоне с заданным шагом по индивидуальному заданию.
Таблица 11
| № варианта | Система уравнений | Диапазон изменения аргумента | Шаг изменения Аргумента Dх |
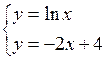 | хÎ[0,2;3] | Dx=0,2 | |
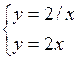 | хÎ[0,2;3] | Dx=0,2 | |
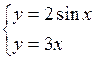 | хÎ[0;2] | Dx=0,1 | |
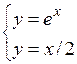 | хÎ[0,2;3] | Dx=0,1 | |
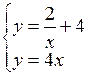 | хÎ[0;2] | Dx=0,2 | |
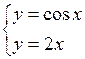 | хÎ[0,2;3] | Dx=0,1 | |
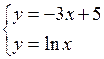 | хÎ[0;2] | Dx=0,2 | |
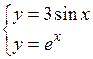 | хÎ[0;2] | Dx=0,1 | |
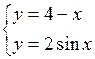 | хÎ[0;2] | Dx=0,1 | |
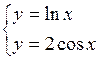 | хÎ[0,2;3] | Dx=0,2 |
Отчет по работе: Распечатка графиков.
13. Приближенное решение уравнений
Цель работы: Изучение работы с процедурой Подбор параметра.
Основные теоретические положения. Нахождение корней уравнения вида f(x) = 0 даже в случае алгебраических уравнений третьей степени достаточно сложно. Поэтому широко используется приближенное решение уравнений.
Обычно применяют итерационные методы, когда сначала выбирают некоторое начальное приближение х(0), затем вычисляют последовательные приближения к истинному значению х.
В Excel для приближенного решения уравнений используются процедуры Подбор параметра и Поиск решений. В данной работе мы познакомимся с использованием процедуры Подбор параметра.
Порядок выполнения работы
Задание 1. Решить уравнение ln x=0.
Задание 2. Решить уравнение х2-3х+2=0.
Задание 3. Решить уравнение согласно индивидуальному заданию.
13.1. Выполнение задания 1
13.1.1. Создать новую рабочую книгу (команды Файл – Создатьпри работесExcel 2003или кнопкаOffice – Создатьпри работе сExcel 2007).
13.1.2. В ячейку А1 введем заголовок Приближенное значение корня.
13.1.3. В ячейку В1 вводим заголовок Левая часть уравнения.
13.1.4. В ячейку А2 вводим первое приближенное значение корня, например число 3.
13.1.5. В ячейку В2 вводим формулу для вычисления левой части уравнения в зависимости от аргумента х: =LN(A2).
Фрагмент получившейся таблицы в режиме показа вычислений приведен в табл. 12, а в режиме показа формул – в табл. 13.
|
Таблица 12
| A | B | |
| Приближенное значение корня | Левая часть уравнения | |
| 1,098612289 |
13.1.6. Для получения приближенного решения уравнения обратимся к процедуре Подбор параметра.
а) Для вызова процедуры Подбор параметра выполнить команды Сервис – Подбор параметра(при работе сExcel 2007выполняем команды: менюДанные –вкладкаРабота с данными – Подбор параметра).
б) в появившемся диалоговом окне Подбор параметра ввести:
Установить в ячейке В2
Значение 0
Изменяя значение ячейки А2
и щелкнуть по кнопке Ок;
в) в появившемся диалоговом окне Результат подбора параметра щелкнем по Ок,чтобы сохранить полученные результаты.
В ячейке А2 получаем приближенное значение корня х=0,999872.
При этом погрешность решения показана в ячейке в ячейке В2: вместо 0 (значение правой части уравнения при его решении) там находится значение
– 0,00013.
Если округлить корень, получим х = 1, что и является известным аналитическим решением уравнения ln x = 0.
13.2. Выполнение задания 2
При решении уравнения х2 – 3х + 2 = 0 очевидно, что должны быть получены два корня. Значит, придется дважды задавать начальное приближение корня и обращаться к процедуре Подбор параметра.
13.2.1. Открыть новый рабочий лист (щелчок правой клавишей мыши по имени любого листа - Добавить - Лист).
13.2.2. В ячейку А1 ввести заголовок Приближенное значение первого корня.
13.2.3. В ячейку В1 ввести заголовок Приближенное значение второго корня.
13.2.4. В ячейку С1 внести заголовок Левая часть уравнения.
13.2.5. В ячейку А2 внести ориентировочное значение первого корня, например, число +3.
13.2.6. В ячейку С2 вводим формулу для вычисления левой части уравнения:
=А2^2-3*A2+2
13.2.7. Вызвать процедуру Подбор параметра:
а) Сервис – Подбор параметра (Данные –вкладкаРабота с данными – Подбор параметра);
б) ввести:
Установить в ячейке С2
Значение 0
|
щелкнуть по Ок;
в) щелкнуть по Ок в окне Результат подбора параметра.
В ячейке А2 получим приближенное значение первого корня х1=2,000048. При этом точность решения (значение правой части уравнения) показана в ячейке С2: вместо 0 получаем число 4,85Е-05 (т. е. 0,0000485).
13.2.8. Для нахождения второго корня в ячейку В2 внести его ориентировочное значение, например число –3, а в ячейку С2 вводим формулу =В2^2-3*В2+2.
13.2.9. Повторить процедуру поиска приближенного решения уравнения:
а) Сервис – Подбор параметра (Данные –вкладкаРабота с данными – Подбор параметра);
б) ввести:
Установить в ячейке С2
Значение 0
|
щелкнуть по Ок;
в) щелкнуть по Ок в окне Результат подбора параметра.
В ячейке В2 получим приближенное значение второго корня: х2=0,9996.
13.3. Выполнение задания 3
13.3.1. Выбрать из табл. 14 индивидуальное задание согласно указанию преподавателя.
13.3.2. Добавить новый лист
13.3.3. Найти корни уравнения по индивидуальному заданию.
Таблица 14
| № варианта | Уравнение | № варианта | Уравнение |
| х3-3х2+х=0 | х3+х2-6х=0 | ||
| х3-7х+6=0 | х3+0,5х2-3,5х-3=0 | ||
| х3+2х2-5х-6=0 | х3+0,5х2-3х=0 | ||
| х3+3х2-4х-12=0 | х3-1,5х2-2,5х+3=0 | ||
| х3-х2-8х-12=0 | х3-3,5х2-1,5х+9=0 |
Отчет по работе: Распечатки таблиц с найденными значениями корней уравнений.