Функции для операции с матрицами

Прямоугольная таблица чисел

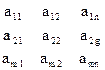
состоящая из m-строк и n-столбцов, называется матрицей размера mхn. Если m=n, то матрица называется квадратной.

Умножение матриц.Умножение матрицы А на матрицу В опре­делено только в том случае, если число столбцов матрицы А равно числу строк матрицы В. В результате умножения получится мат­рица АВ, у которой столько же строк, сколько их в матрице А, и столько же столбцов, сколько их в матрице В.

Пусть даны матрицы А и В (рис. 9.10). Элементы матрицы АВ вычисляются следующим образом:

аb₁₁= (2,3,4,5)(3,4,l,2)=2∙3+3∙4+4∙l+5∙2=32;
ab₁₂=(2,3,4,5)(2,-l,-3,5)=2∙2+3∙ (-l)+4∙ (-3)+5∙5=14;

ab₂₁=(9,2,-3,4)(3,4,l,2)=40 и т.д.

	А	В	С	D	Е
	А=			-3
		-1
	В=		-1
	АВ=

Рис. 8.10. Пример умножения матриц

Для умножения двух матриц в Excel имеется функция

МУМНОЖ(матрица1;матрица2) (MMULT(arrayl,array2)).

Для нахождения произведения двух матриц в Excel необходи­мо:

• выделить область, где будет размещена матрица произведений двух матриц;

• найти функцию МУМНОЖ;

• указать диапазон первой и второй матриц;

• нажать клавишу «Готово».

Затем следует нажать клавишу F2 и нажать клавиши «Ctrl»+«Shift»+«Enter».В выделенной области появится результат от умножения двух матриц. Формула при этом будет заключена в фигурные скобки.

Обращение матриц.Квадратная матрица вида

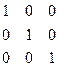
называется единичной и обозначается через Е.

Квадратная матрица А называется обратимой, если можно по­добрать такую матрицу В, что А∙В = В∙А = Е. Матрица В называет­ся обратной матрицей для матрицы А. Обратную матрицу обозна­чают через А^-1.

Матрицу называют невырожденной, когда ее столбцы линейно независимы. Квадратная матрица обратима тогда и только тогда, когда она невырожденная.

Для обращения матриц в Ехсе1 имеется функция: МОБР(массив) (MINVERSE{array)).

Пример. Пусть нам дана исходная матрица А (рис. 9.11). Для ее обращения проделаем следующее:

• выделим область B6:D8;

• вызовем функции МОБР и зададим аргумент B1:D3;

• щелкнем по клавише «Готово»;

• перейдем в режим редактирования, нажав F2;

• нажмем клавиши «Ctrl»+«Shift»+«Enter».

В результате получим матрицу, обратную А.

	А	В	С	D
				-1
	А=
		-1	-1
		1,142857	0,142857	0,428571
	А-1=	-0,857143	0,142857	-0,571429
		0,142857	0,142857	0,428571

Рис. 8.11. Пример обращения матрицы

Задание 1.

С помощью встроенных функций Excel:

1) перемножьте матрицы 1 и 2;

2) найдите сумму чисел второго и третьего столбцов полученной матрицы (Внимание! При нахождении суммы матрицу желательно ввести заново);

3) найдите сумму квадратов всех чисел для первого столбца полученной матрицы;

4) найдите произведение всех чисел для второго столбца полученной матрицы;

5) найдите обращенную матрицу для 1 матрицы;

6) округлите числа первой строчки вверх по модулю до ближайшего четного числа.

Вариант 1		Матрица 1			Матрица 2
	6,40	4,17	2,31				2,30	7,12	6,28
	3,65	5,62	6,27				4,93	4,23	3,24
	9,45	4,36	8,12				6,34	1,89	2,89
Вариант 2		Матрица 1			Матрица 2
	7,56	3,12	9,31				7,30	6,32	7,21
	2,65	7,12	2,27				2,34	5,23	6,24
	5,23	5,25	11,12				1,34	7,45	2,11
Вариант 3		Матрица 1			Матрица 2
	2,22	8,17	9,11				6,40	2,62	5,28
	4,15	9,67	11,67				4,53	5,83	7,24
	1,49	3,56	3,12				6,34	1,39	2,89
Вариант 4		Матрица 1				Матрица 2
	6,56	4,12	4,31				6,30	2,32	4,21
	8,65	3,12	8,27				3,38	8,46	6,27
	1,23	1,25	4,12				8,34	7,45	4,11
Вариант 5		Матрица 1				Матрица 2
	2,40	8,17	8,31				7,30	9,12	3,28
	7,65	3,62	4,27				3,93	3,23	6,24
	5,45	2,36	8,12				6,34	6,89	4,89

Задание 2.

С помощью встроенных функций Excel:

1) найдите сумму всех чисел, больших 5, в массиве;

2) вычислите сумму квадратов разностей (первый столбец принять за Х, второй столбец принять за У);

3) найти полусумму всех значений массива.

Вариант 1		Вариант 2		Вариант 3		Вариант 4
Массив		Массив		Массив		Массив

Вариант 5
Массив

Задание 3.

С помощью встроенных функций Excel решите следующие примеры:

1) вычислите абсолютное значение для числа А;

2) вычислите натуральный логарифм от аргумента N;

3) возведите число В в степень С;

4) вычислите ;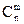

5) вычислите факториал К.

№ варианта	А	N	В	С	m	n	К
	-5668
	-7634
	-9369
	-2581