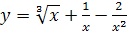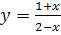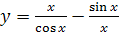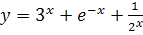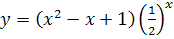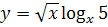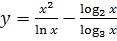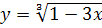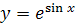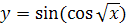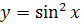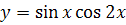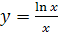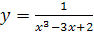Основные правила дифференцирования

Наименование	Функция	Производная
умножение на постоянный множитель   сумма (разность) двух функций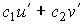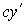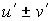
Произведение двух функций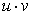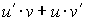
Частное двух функций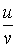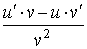
Сложная функция	y=F(u), u=φ(x)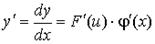
Обратная функция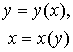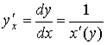

Производные основных элементарных функций

№ п/п	Наименование функции	Функция и её производная
	константа	(c)’=0
	степенная функция   частные случаи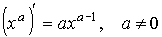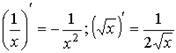
	показательная функция частный случай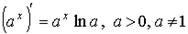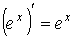
	логарифмическая функция   частный случай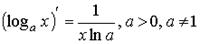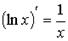
	тригонометрические функции	; ; ; ;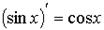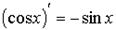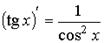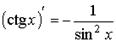
	обратные тригонометрические функции	; ; ;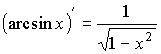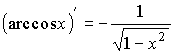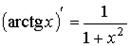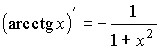

Производная n-го порядка (n-ая производная ) функции y=f(x):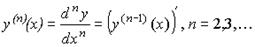

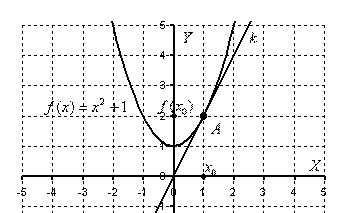
Уравнение касательной.

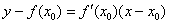
Задания.

№ 1. Вычислить 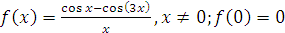при х=0 и в произвольной точке

№ 2. Найти производные следующих функций:

1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 
10. 

№ 3. Найти производные второго порядка следующих функций:

1. 
2. 
3. 
4. 
5. 
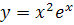
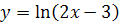
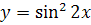
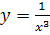
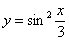
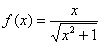6. . Найти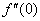

№ 4. Найти производные n-го порядка следующих функций:

1. 
2. 
3. 
4. 

№ 5. Построить касательную графика функции

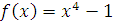1. в точке (0, -1)
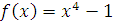2. в точке (1, 0).
3. в точке с абсциссой .
4. в точке с абсциссой
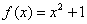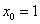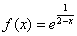5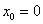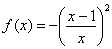. в точке с абсциссой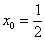

Занятие 13.

Тема занятия: «Исследование функций одной переменной.»

План занятия.

1. Знакомство с теоретическим материалом.
2. Разбор заданий под руководством преподавателя.
3. Самостоятельное выполнение заданий.

Методические материалы.

Аналитическое представление функции в явном виде: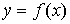

Четность функции

Четная функция: .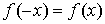

Нечетная функция: .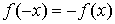

Периодичность

Периодическая функция: 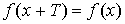, где T – период функции, .

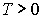Ограниченность функции.

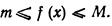
Непрерывность функции.

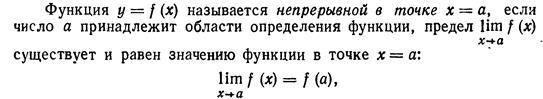
Монотонность функции.

План исследования функции(в элементарной математике):

1. Элементарное исследование:

- найти область определения и область значений;

- выяснить общие свойства: четность(нечетность), периодичность;

- найти точки пересечения с осями координат;

- определить участки знакопостоянства.

2. Исследование с помощью производной:

- найти критические точки;

- определить интервалы возрастания и убывания функции;

- определить экстремумы.

3. Построение графика функции.

Рекомендации по применению плана исследования функции:

1. Отдельные элементы исследования наносятся на график постепенно, по мере их нахождения.

2. Если появляются затруднения с построением графика функции, то находятся значения функции в некоторых дополнительных точках.

3. Целью исследования является описание характера поведения функции, поэтому строится не точный график, а его приближение, на котором четко обозначены найденные элементы (экстремумы, точки перегиба, асимптоты и т.д.).

4. Строго придерживаться приведенного плана необязательно; важно не упустить характерные элементы поведения функции.

Задания.

Найти область определения функции:

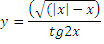
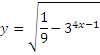
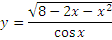
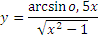
Найти область значений функции

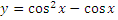
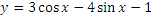
Найти сумму целых значений функции

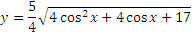
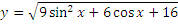
Определить является четной или нечетной функция

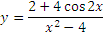
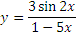
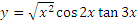
Найдите нули функции, промежутки знакопостоянства, возрастания и убывания

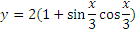
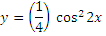
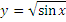
Занятие 14.

Тема занятия: «Неявно заданная функция. Параметрически заданная функция.»

План занятия.

1. Знакомство с теоретическим материалом.
2. Разбор заданий под руководством преподавателя.

Методические материалы.

Неявно заданная функция.

Функция вида F(x, y) = 0 называется неявно заданной.

Если F(x,y) можно разложить на множители 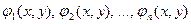, то данному уравнению соответствует система кривых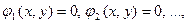 .
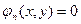