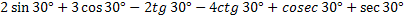Обратные тригонометрические функции

Обра́тные тригонометри́ческие фу́нкции (круговые функции, аркфункции) — математические функции, являющиеся обратными к тригонометрическим функциям. К обратным тригонометрическим функциям обычно относят функции:

аркси́нус (обозначение: arcsin)

аркко́синус (обозначение: arccos)

аркта́нгенс (обозначение: arctg; в иностранной литературе arctan)

арккота́нгенс (обозначение: arcctg; в иностранной литературе arccot или arccotan)

Арксинус y=Arcsinxопределен для 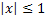, многозначна.Другие значения y=Arcsinxвыражаются черезглавное его значение формулой 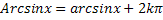. Следовательно, область определения y=аrcsinx – [­-1;1]; область значений [ 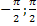]. Функция y=аrcsinxнечетная, на [­1;1] монотонно возрастает от 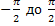. График функции проходит через (0,0). Эта точка является и точкой перегиба графика. На [-1;0] функция выпуклая, на [0,1]- вогнутая.

Арккосинус y=Arccosxопределен для 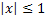, многозначна.Другие значения y=Arccosxвыражаются черезглавное его значение формулой 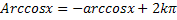. Область определения y=аrccosx – [­1;1]; область значений [ 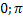]. Функция y=аrccosxна [­-1;1] монотонно убывает от 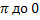. Дляy=аrccosxвыполняется неравенство аrccos(-x)=π-аrccosx . График функции проходит через (0, 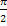). Эта точка является и точкой перегиба и центром симметрии кривой. На [-1;0] функция вогнутая, на [0,1]- выпуклая.

Арктангенс y=Arctgxопределен для 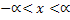, многозначна.Другие значения y=Arctgxвыражаются черезглавное его значение формулой 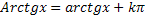. Область определения y=аrctgx – [-∞; ∞]; область значений от 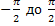.Функция y=аrctgxнечетная. Функция y=аrctgxна [-∞; ∞] монотонно возрастает от 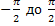. График функции проходит через (0,0). Эта точка является и точкой перегиба и центром симметрии кривой. На [-∞;0] функция вогнутая, на [0,∞]- выпуклая.

Арккотангенс y=Arсctgxопределен для 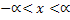, многозначна.Другие значения y=Arсctgxвыражаются черезглавное его значение формулой 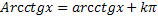. Область определения y=аrсctgx – [-∞; ∞]; область значений от 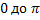.Функция y=аrcсtgxна [-∞; ∞] монотонно убывает от 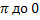.Дляy=аrcctgxвыполняется неравенство аrcctg(-x)=π-аrcctgx . График функции проходит через (0,0). Эта точка является и точкой перегиба и центром симметрии кривой. На [-∞;0] функция выпуклая, на [0,∞]- вогнутая.

Графики функций

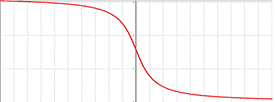
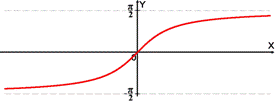
arccos x arcsin x

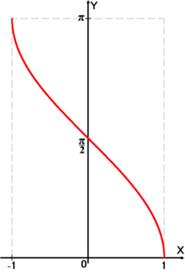
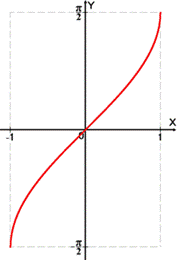
arcctg x arctg x

Свойства обратных тригонометрических функций

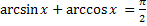
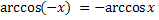
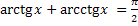
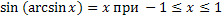
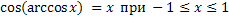
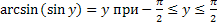
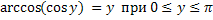
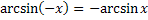
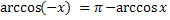
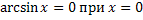
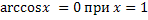
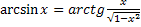
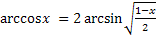
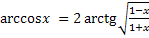
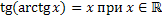
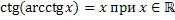
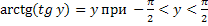
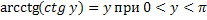
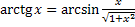
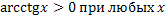
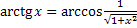
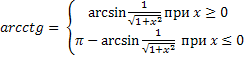
Задания.

№ 1. Построить графики функций:

1. y=cos2x
2. y=sin(x-П/3)
3. y=tgx/3
4. y=ctg(2x+П/3)

№ 2. Вычислить:

1.

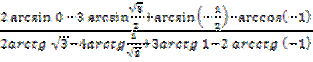
2.

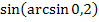
3.

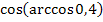
4.

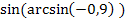
5.

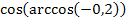
6.

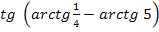
№ 3. Выяснить, какое из следующих двух чисел больше

1.

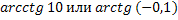
2.

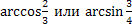
Занятие 9.

Тема занятия: «Основные свойства и формулы. Преобразование тригонометрических выражений.»

План занятия.

1. Знакомство с теоретическим материалом.
2. Разбор заданий под руководством преподавателя.
3. Самостоятельное выполнение заданий.

Методические материалы.

Основные тригонометрические свойства.

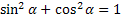
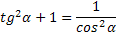
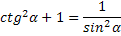
Формулы сложения аргументов

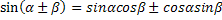
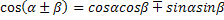
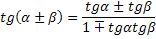
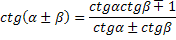
Формулы двойного угла

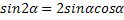
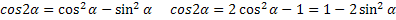
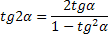
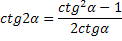
Формулы понижения степени

Синус	Косинус	произведение

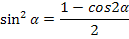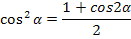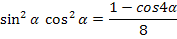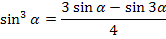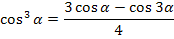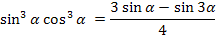Формулы преобразования произведений функций

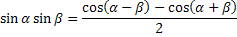
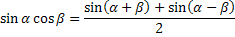
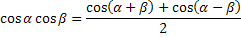
Формулы преобразования суммы функций

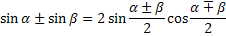
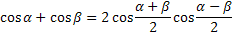
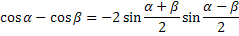
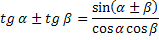
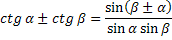
Задания.

№ 1. Вычислить.

1. 
2. 
3. 

№ 2. Найти значение

1.

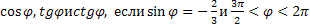
2.

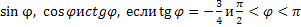
№ 3. Вычислить без помощи таблиц

1.

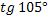
2.

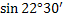
3.

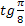
4.

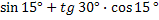
Занятие 10.

Тема занятия: «Показательная функция. Показательные уравнения и неравенства.»

План занятия.

1. Знакомство с теоретическим материалом.
2. Разбор заданий под руководством преподавателя.
3. Самостоятельное выполнение заданий.

Методические материалы.

Определение. Функцию вида 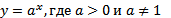называют показательной функцией.
Основные свойства показательной функции у =а^x

Свойства функции.

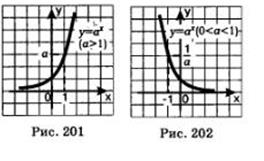
a>1	0<a<1
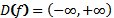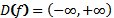E(f)=(0,+ 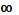)	E(f)=(0,+ )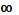
не является ни четной, ни нечетной
Возрастает	Убывает
Непрерывна	Непрерывна
не ограничена сверху, ограничена снизу
выпукла вниз.
ось х является горизонтальной асимптотой графика.

Графики функции.