Методические указания к проведению практических занятий
Занятие 1.
Тема занятия: «Множества. Числовые множества. Элементы теории множеств.»
План занятия.
- Знакомство с теоретическим материалом.
- Разбор заданий под руководством преподавателя.
- Самостоятельное выполнение заданий.
Методические материалы.
Способы задания множеств:
1) перечислением.
2) указанием характеристического свойства, т.е. такого свойства, что элементы множества им обладают, а все остальное на свете не обладает.
Диаграммы Венна.
Равенство множеств: A=B: "x xÎAÛxÎB.
Пустое множество: множество, не имеющее ни одного элемента, обозначают Æ.
Универсальное множество. Обычно все множества, с которыми имеют дело в том или ином рассуждении, являются подмножествами некоторого фиксированного множества I. Мы будем называть в этом случае множество I универсальным множеством.
Подмножество. Множество B является подмножеством другого множества A, если каждый элемент x из B является вместе с тем и элементом множества A. обозначают BÌA.
Числовые множества. Примерами таких множеств могут служить:
а) множество всех натуральных чисел,
б) множество всех целых чисел (положительных, отрицательных и нуля),
в) множество всех рациональных чисел,
г) множество всех действительных чисел.
Пересечение множеств. Множество, состоящее из общих элементов множеств A, B, называется пересечением этих множеств или их произведением. Пересечение двух множеств A и B обозначается AB или AÇB. Решение систем уравнений и неравенств, по сути дела, сводится к отысканию пересечения некоторых множеств.
Объединение (сложение) множеств. Суммой множеств A, B называют новое множество, состоящее из тех и только тех элементов, которые входят хоть в одно из слагаемых множеств (в объединении повторяющиеся элементы считаются лишь по одному разу). Сумму множеств A и B обычно обозначают A+B или AÈB.
Вычитание множеств. Разностью двух множеств A и B называют новое множество, обозначаемое A−B или A\B, в которое входят все элементы множества A, не принадлежащие B. Вычитание B из A сводится к удалению из A общей части A и B: A−B=A−AB.
Дополнение множества. Если все множества рассматриваются как подмножества универсального множества I, то обычно под дополнением множества B понимают его дополнение в I. В этом случае вместо B'_I пишут просто B'.
Задания.
1 (уст). Из примеров множеств укажите, которые заданы перечислением или их можно так задать. Приведите свои примеры. ({понедельник, вторник, среда, четверг, пятница, суббота, воскресенье}, множество арифметических действий, множество корней квадратного уравнения x^2−2x−24=0 {−4, 6})
2 (уст). Из выше приведенных примеров множеств укажите, которые заданы характеристическим свойством. Приведите свои примеры.
3. Установите связь между числовыми множествами.
4. Что является решением уравнения (x^2 +y^2 −37)(y −x−7)=0? Ответ: множество, состоящее из окружности и прямой.
5.Данная задача, связанная с подсчетом численности конечных множеств, принадлежит известному детскому писателю Льюису Кэрроллу, автору .Алисы в стране чудес. Под псевдонимом Льюис Кэрролл писал математик Доджсон. В одной из повестей Кэрролла есть следующая задача:
В ожесточенном бою 70 из 100 пиратов потеряли один глаз, 75 — одно ухо, 80 — одну руку и 85 — одну ногу. Каково минимальное число потерявших одновременно глаз, ухо, руку и ногу?
Решение. Обозначим через A множество одноглазых, через B — множество одноухих, через C — множество одноруких и через D — множество одноногих. В задаче требуется оценить численность множества ABCD. Ясно, что все универсальное множество I можно представить как сумму этого множества ABCD и множества пиратов, сохранивших либо оба глаза, либо оба уха, либо обе руки, либо обе ноги. Поэтому I =A' +B' +C' +D' +ABCD. Отсюда следует, что численность множества I не больше суммы численностей множеств A', B', C', D' и ABCD (она была бы равна этой сумме, если бы множества A', B', C' и D' попарно не пересекались). Но численность множества A' равна 30, множества B' — 25, множества C' — 20 и множества D' — 15. Так как численность'универсального множества равна 100, то имеем 100<=30+25+20 +15+N(ABCD). Отсюда
N(ABCD)>=100−30−25−20−15=10.
Итак, не менее 10 пиратов лишились и глаза, и уха, и руки, и ноги.
6. Множество A состоит из целых чисел, делящихся на 4, множество B — из целых чисел, делящихся на 10, и множество C из целых чисел, делящихся на 75. Из каких чисел состоит множество ABC?
7. В библиотеке есть книги по разным отделам науки и искусства. Обозначим множество всех книг в библиотеке через A, а множество всех математических книг (не только в данной библиотеке) — через B. Охарактеризуйте множество A — B.
8. Множество A состоит из точек M(x; y) плоскости, для которых |x|64, |y|64, множество B — из точек плоскости, для которых x2 +y2 625, и множество C — из точек плоскости, для которых x>0. Изобразите множество AB −C.
Занятие 2.
Тема занятия: «Множества. Числовые множества. Элементы теории множеств.»
План занятия.
- Знакомство с теоретическим материалом.
- Разбор заданий под руководством преподавателя.
- Самостоятельное выполнение заданий.
Методические материалы.
Алгебра множеств.
Мы познакомились с основными действиями над множествами — сложением, вычитанием и умножением (пересечением) множеств. Эти действия обладают целым рядом свойств, напоминающих свойства действий над числами.
Роль нуля и единицы в действиях над множествами играют множества Æ (пустое множество) и I (универсальное множество).
Приведем список свойств действий над множествами:
1) AÌA.
2) Если AÌB и BÌA, то A=B.
3) Если AÌB и B ÌC, то AÌC.
4) ÆÌA.
5) AÌI.
6) A+B =B +A.
7) AB =BA.
8) A+(B +C)= (A+B)+ C.
9) A(BC)= (AB)C.
10) A+A=A.
11) AA=A.
12) A(B +C)=AB +AC.
13) A+BC =(A+B)(A+C).
14) A+Æ=A.
15) AI =A.
16) A+I =I.
17) AÆ=Æ.
18) Соотношение AÌB эквивалентно каждому из соотношений A+B =B, AB =A.
19) A+A'=I.
20) AA'=Æ.
21) Æ'=I.
22) I' =Æ.
23) (A')'=A.
24) Соотношение AÌB эквивалентно B'ÌA'.
25) (A+B)' =A'B'.
26) (AB)0 =A' +B'.
Отметим следующее замечательное .соотношение двойственности. Если в каждом из свойств 1)–26) заменить друг на друга символы Ì и É, Æ и I, È и Ç, то в результате получится снова одно из этих свойств.
Задания.
1. Упростить далее выражение (A+B)^2 =A^2 +B^2 +2AB. Ответ: A+B.
2. Доказать распределительный закон для множеств A+BC =(A+B)(A+C).
3. Доказать A+(B−C)НЕ=(A+B)−C для случая A=B=C.
Решение. A+B =A и потому (A+B)−C=A−A=Æ — пустое множество, а A+(B−C)=A+Æ=A
4. Доказать следующие формулы: (A+B)' =A'B' и (AB)' =A' +B' (на диаграмме).
5. Пользуясь правилами алгебры множеств, упростите выражение (A+B+C)(A+B)−[A+(B−C)]A.
6. Докажите равенства
а) (A−B)−C =(A−C)−(B −C);
б) (A−B)+(B −C)+ (C −A)+ ABC =A+B +C.
7. Докажите включение мноржеств AC +BD _(A+B)(C +D);
8. Вытекает ли из A−B =C, что A=B +C?
9. Вытекает ли из A=B +C, что A−B =C?
10. Какие включения справедливы для множеств A−(B +C) и (A−B)−C?
11.Упростите выражение [(X−Y)’(X’ +Y’)]’.
Занятие 3.
Тема занятия: «Делимость многочленов, деление с остатком. Симметрические многочлены и основная теорема. Неприводимые многочлены. Многоугольник Ньютона и критерий Дарбу о неприводимости. Наибольший общий делитель двух многочленов. Алгоритм Евклида.»
План занятия.
- Знакомство с теоретическим материалом.
- Разбор заданий под руководством преподавателя.
- Самостоятельное выполнение заданий.
Методические материалы.
Многочлен n-ной степени от неизвестного х:
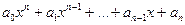
Для сокращенной записи многочленов употребляются символы f(x), g(x) и так далее.
