Модуль вектора. Направляющие косинусы

Рассмотрим в пространстве прямоугольную систему координат Oxyz. Выделим на координатных осях Ox, Oy и Oz единичные векторы (орты), обозначаемые соответственно, т.е. .

Выберем произвольный вектор 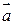пространства и совместим его начало с началом координат: .

Найдем проекции вектора 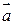на координатные оси. Проведем через конец вектора плоскости, параллельные координатным плоскостям. Точки пересечения этих плоскостей с осями обозначим соответственно через . Получим прямоугольный параллелепипед, одной из диагоналей которого является вектор . Тогда , , . По определению суммы нескольких векторов находим . А так как , , то

Но , , .

Обозначим проекции вектора на оси Ox, Oy и Oz соответственно через , и , т.е. , и .

Тогда получаем

. (2.1)

Формула (2.1) является основной в векторном исчислении и называется разложением вектора по ортам координатных осей. Числа , и называются координатами вектора 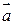, т.е. координаты вектора есть его проекции на соответствующие координатные оси. Векторное равенство (2.1) часто записывается в символическом виде: .

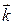Единичные вектора и в 3-х-мерном пространстве имеют соответствующие координаты: , , .

Зная проекции вектора 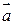, можно легко найти выражение для модуля вектора. На основании теоремы о длине диагонали прямоугольного параллелепипеда можно записать , т.е.

.

Отсюда

, (2.3)

т.е. модуль вектора равен квадратному корню из суммы квадратов его проекций на оси координат.

Если вектор находится на плоскости , то модуль вектора находится по формуле:

. (2.4)

Пусть углы вектора 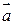с осями Ox, Oy и Oz соответственно равны a, b и g. По свойству проекции вектора на ось имеем

, , .

Или,

. (2.5)

Числа называются направляющими косинусами вектора .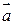

Подставляя полученные косинусы в выражение квадрата модуля вектора 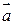, получаем

.

Сократив на , получаем соотношение

, (2.6)

т.е. сумма квадратов направляющих косинусов ненулевого вектора равна единице.

Легко заметить, что координатами единичного вектора (орта) являются числа , т.е. .

Итак, задав координаты вектора, всегда можно определить его модуль и направление, т.е. сам вектор.

Мы видим, что вектор можно представить как упорядоченная совокупность двух чисел, если вектор находится на плоскости, т.е. ; как совокупность трех чисел, если вектор находится в 3-х-мерном пространстве, т.е. .

Но в математике и ее приложениях часто приходиться изучать такие объекты, для задания которых недостаточно двух или трех действительных (вещественных) чисел. Например, положение твердого тела в пространстве определяется совокупностью шести вещественных чисел: три координаты его центра масс, два угла, характеризующие направление некоторой фиксированной оси, проходящей через центр масс, и, наконец, угол поворота вокруг этой оси. Этот пример свидетельствует о целесообразности обобщения понятия вектора на случай любой конечной упорядоченной совокупности вещественных чисел.

Определение 2.1. Упорядоченная совокупность n вещественных чисел называется n-мерным вектором, а числа - координатами вектора, т.е.

.

Смысл требования упорядоченности состоит в том, что если переставить любые два неравных числа в этой совокупности, то получится другая совокупность, отличная от исходной. Как правило, векторы записывают строкой, но иногда необходимо записать вектор столбцом, т.е.

.

Можно сказать, что множество всех n-мерным векторов находится в так называемом -мерном пространстве (корректно понятие будет введено ниже).

Алгебраический вектор, как мы видели выше, можно представить в виде разложения по единичным векторам, т.е.

(на плоскости );

(в 3-х-мерном пространстве).

Аналогично можно разложить вектор по единичным векторам в -мерном пространстве.

Пусть ,

,

,

…………………..

.

единичные векторы n-мерного пространства.

Тогда вектор можно представить в виде разложения по единичным векторам следующим образом:

. (2.7)

2.2.Действия над векторами, заданными координатами

Пусть векторы 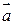и 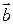заданы своими координатами или проекциями на оси координат Ox, Oy и Oz, т.е.

и

.