Приложения геометрического вектора
Доказательство.
,
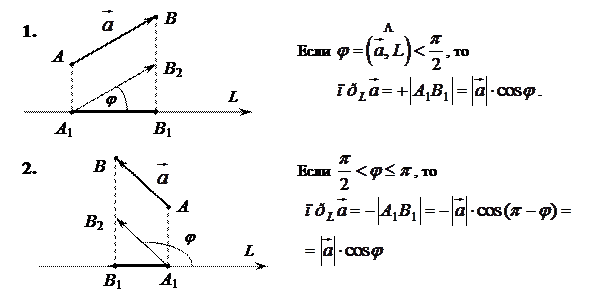
Следствие 1.1. Проекция вектора на ось положительная (отрицательная), если вектор образует с осью острый (тупой) угол, и равна нулю, если этот угол – прямой.
Следствие 1.2. Проекции равных векторов на одну и ту же ось равны между собой.
Свойство 2. Проекция суммы нескольких векторов на одну и ту же ось равна сумме их проекций на эту ось, т.е.
.
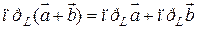Свойство 3. При умножении вектора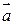 
на число l его проекция на ось также умножается на это число, т.е.
.
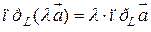Таким образом, линейные операции над векторами приводят к соответствующим линейным операциям над проекциями этих векторов.
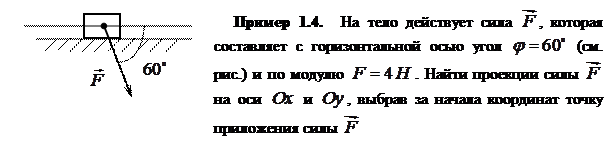
Решение.
Выбираем произвольно оси координат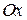 
и 
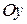, где точка 
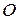− начала системы координат.
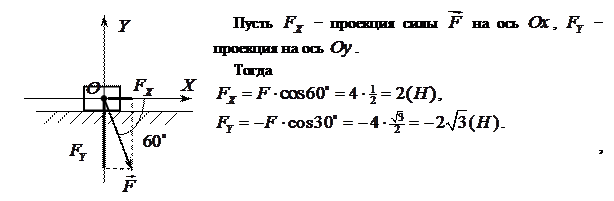
Приложения геометрического вектора
Декартовы прямоугольные координаты вектора.
Линейные операции над векторами
Линейные операции над векторами сводятся к соответствующим линейным операциям над проекциями этих векторов.
1. При сложении (вычитании) векторов их одноименные координаты складываются (вычитаются), т.е.
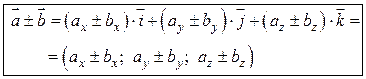. (2.8)
2. При умножении вектора на скаляр координаты вектора умножаются на этот скаляр, т.е.
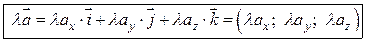. (2.9)
Равенство векторов
Из определения вектора как направленного отрезка, который можно передвигать в пространстве параллельно самому себе, следует, что два вектора 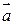и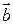 
равны тогда и только тогда, когда выполняются равенства: 
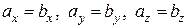, т.е.
.
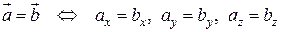Операции сумма, разность двух векторов и умножение вектора на число, а также и равенство векторов, можно обобщить на n-мерный вектор.
Пример 2.1. Найти координаты и длину вектора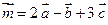 
, если 
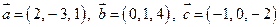. Найти координаты орта вектора 
.
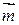Решение. Согласно формулам (2.8) и (2.9) находим координаты вектора :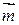
.
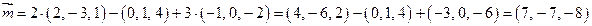По формуле (2.3) находим длину вектора :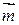
.
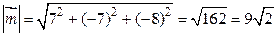Координаты орта (единичного вектора) вектора 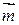находятся по следующим формулам:
,
, 
, 
.
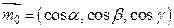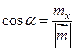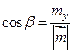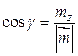Тогда получаем
, 
, 
.
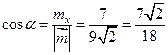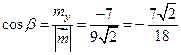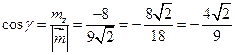Таким образом,
,
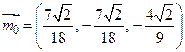
Коллинеарность векторов
Выясним условие коллинеарности векторов 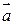и 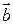, заданных своими координатами.
Так как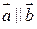 
, то можно записать 
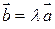, где l - некоторое действительное число. То есть
.
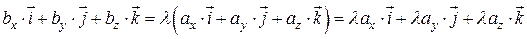Отсюда
,
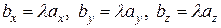т.е.
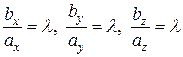или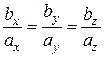 
.
Значит, координаты коллинеарных векторов пропорциональны. Верно и обратное утверждение: векторы, имеющие пропорциональные координаты, коллинеарны.
Таким образом, два вектора 
и 
коллинеарны тогда и только тогда, когда их координаты соответственно пропорциональны, т.е.
.
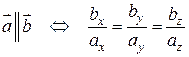Пример 2.2. Коллинеарны ли векторы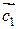 
и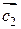 
, построенные на векторах 
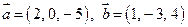, есл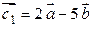и 
и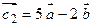 
?
Решение. Коллинеарность векторов 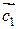и 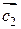означает пропорциональность их координат. Имеем
, 
.
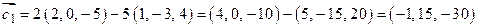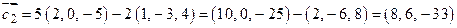Так как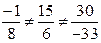 
, т.е. координаты векторов и 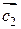не пропорциональны, следовательно, эти векторы не коллинеарны.
,
Радиус-вектор. Координаты точки.
Решение.
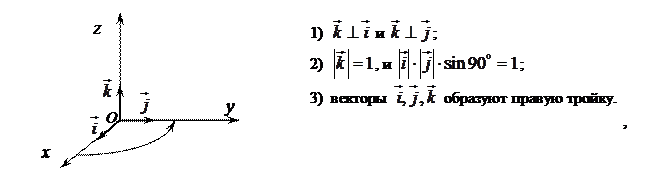
Линейно зависимые и линейно независимые
Системы векторов
Выше были введены операции над векторами, находящимися на плоскости (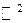 
) или в 3-х-мерном пространстве ( 
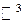). Так же было определено понятие «n-мерный вектор», и введены операции над ними в n-мерном пространстве.
Если мы в n-мерном пространстве рассматриваем точку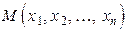 
, то этой точке можно поставить в соответствие радиус-вектор 
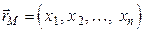. Можно сформулировать и обратное утверждение: каждому радиус-вектору 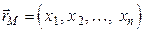ставиться в соответствие точка 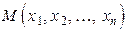, т.е.
.
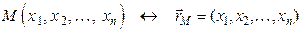Теперь можно ввести корректное понятие «n-мерное векторное пространство».
Определение 6.1. Множество всех n-мерных векторов, в котором для любых двух векторов определена их сумма, и для любого действительного числа определено произведение вектора на это число, называется действительнымn-мерных векторным арифметическим пространством 
.
Если в n-мерном векторном пространстве введена операция скалярного умножения, то оно называется евклидовым пространством.
Надо отметить, что любую совокупность векторов 
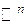пространства можно считать как систему векторов.
Для характеристики взаимного расположения векторов в пространстве вводится понятие линейной зависимости между векторами.
Определение 6.2. Вектор 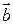называется линейной комбинациейвекторов системы 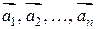, если существуют такие числа 
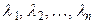, что
. (6.1)
Числа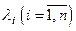 
называются коэффициентами линейной комбинации. В этом случае говорят, что вектор 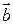линейно выражается через систему векторов 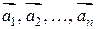или вектор 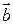разложен по векторам системы 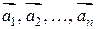. Введением понятия линейной комбинации мы объединили понятия сложения векторов и умножения вектора на число.
Определение 6.3. Система векторов 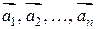называется линейно зависимой, если существуют такие числа 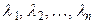, из которых хотя бы одно отлично от нуля, что
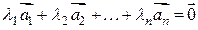. (6.2)
В противном случае векторы 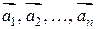называются линейно независимыми.
Приведем теоремы (без доказательства), устанавливающие условия линейной зависимости векторов на плоскости и в 3-х-мерном пространстве.
Теорема 6.1. Любые два коллинеарных вектора линейно зависимы, а два неколлинеарных вектора линейно независимы.
Теорема 6.2. Три компланарных вектора линейно зависимы, а три некомпланарных вектора линейно независимы.
Пример 6.1. Выяснить, будет ли данная система векторов линейно зависимой или независимой
.
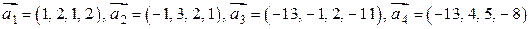Решение. Составим их линейную комбинацию:
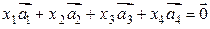
или
.
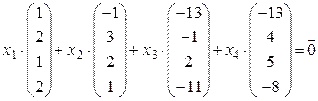Такое векторное уравнение эквивалентно следующей системе уравнений:
.
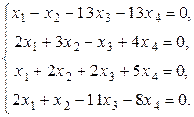Составляем матрицу системы и приводим к ступенчатому виду:
~ 
~ 
.
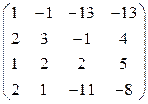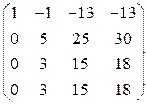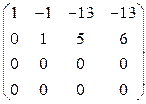Последняя матрица равносильна следующей системе уравнений:
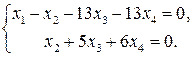
Можно не решая системы уравнений сказать, что система имеет бесчисленное множество решений, среди которых есть ненулевое. Значит, система векторов линейно зависима.
Например, частным решением является: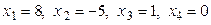 
. Значит, 
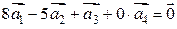, т.е. указанная система векторов линейно зависима.
,
Базис системы векторов.
Доказательство.
,
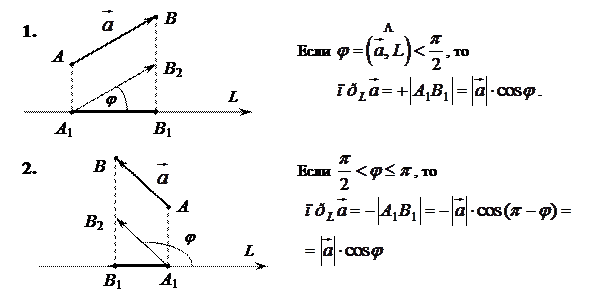
Следствие 1.1. Проекция вектора на ось положительная (отрицательная), если вектор образует с осью острый (тупой) угол, и равна нулю, если этот угол – прямой.
Следствие 1.2. Проекции равных векторов на одну и ту же ось равны между собой.
Свойство 2. Проекция суммы нескольких векторов на одну и ту же ось равна сумме их проекций на эту ось, т.е.
.
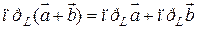Свойство 3. При умножении вектора 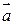на число l его проекция на ось также умножается на это число, т.е.
.
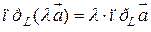Таким образом, линейные операции над векторами приводят к соответствующим линейным операциям над проекциями этих векторов.
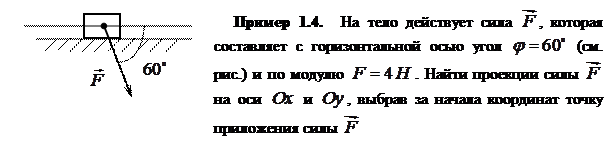
Решение.
Выбираем произвольно оси координат 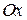и 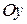, где точка 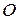− начала системы координат.
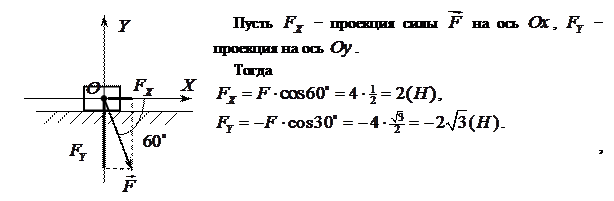
Приложения геометрического вектора