Представление сигналов в виде рядов ортогональных функций

При передаче сообщений одновременно существует большое количество разнообразных сигналов. Допустим, что имеются два сигнала s_i и s_j и определим энергию суммарного сигнала

Видно, что в отличие от самих сигналов, их энергии неаддитивны. Энергия суммарного сигнала содержит так называемую взаимную энергию, которая определяется как скалярное произведение двух вещественных сигналов

(2.11)

Если взаимная энергия сигналов s_i и s_j равна нулю, то они называются ортогональными.

Для исследования различных свойств сообщений, сигналов и помех удобно использовать разложение этих процессов в ряды.

Любой процесс (с некоторыми математическими ограничениями) можно представить в виде ряда:

_, (2.12)

где j_k(t) – ортогональные функции, т.е.:

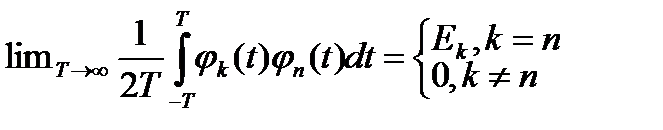
C_k – коэффициенты разложения, Е_k – энергия ортогональных функций.

Если выбрать в качестве ортогональных функций:

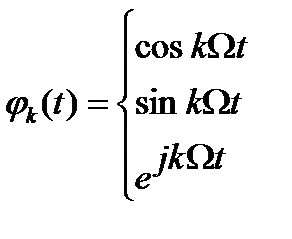
то этот ряд (2.12) называется рядом Фурье (тригонометрический ряд).

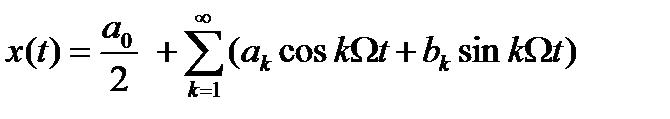(2.13)

W = 2π/Т – частота первой гармоники, определяемая периодом T (T– период функции x(t)).

Другая, эквивалентная формула записи тригонометрического ряда:

(2.14)

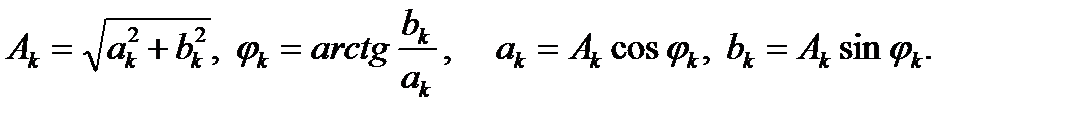
На рис. 2.5 приведены графики, иллюстрирующие представление периодической последовательности прямоугольных импульсов s(t) конечным числом слагаемых (k = 5) ряда Фурье.

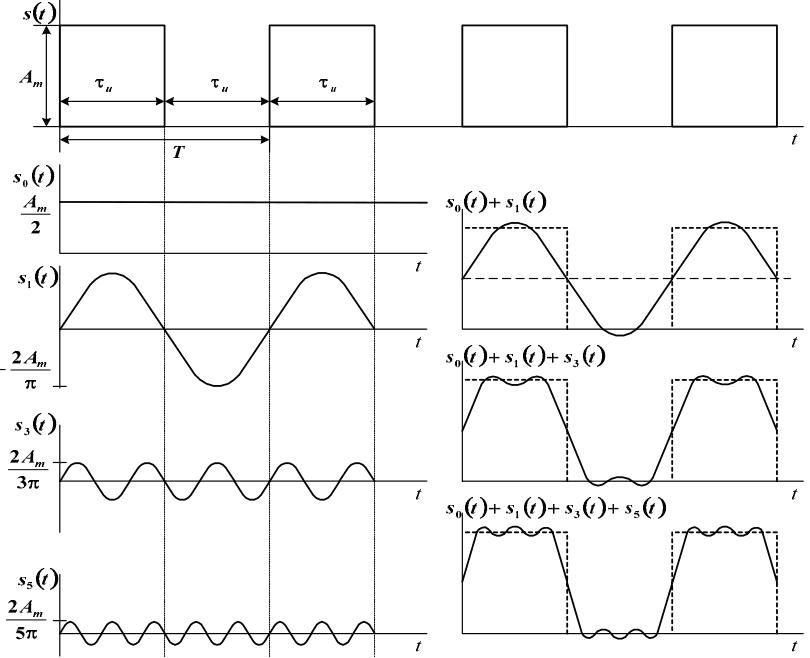
Рис. 2.5. Аппроксимация прямоугольных импульсов суммой гармоник

Для спектрального представления последовательности прямоугольных импульсов начало отсчета целесообразно брать в середине импульса.

Действительно, в этом случае в разложении останутся только косинусоидальные составляющие, так как интегралы от нечетных функций за период равны нулю b_k = 0.

Для четного сигнала x(t) = x(-t), коэффициенты a_k ≠ 0, b_k = 0.

Для нечетного сигнала x(t) = -x(-t), коэффициенты a_k = 0, b_k ≠ 0.

Для функции s(t) (рис. 2.5) разложение имеет вид

(2.15)

Периодическая последовательность прямоугольных импульсов s(t) представляется как результат сложения постоянной составляющей A_m/2 и синусоидальных сигналов с частотами F₁, 3F₁, 5F₁, …, причем период синусоиды с частотой F₁ совпадает с периодом последовательности импульсов s(t) . Для удобства F₁ можно представить в виде F₁ = Ω₁/2π = 1/T.

Легко заметить, что график суммы двух первых слагаемых разложения (2.15) воспроизводит форму графика функции s(t) очень грубо, только в основных чертах. Учет третьего слагаемого существенно улучшает совпадение суммы с функцией s(t). Таким образом, с увеличением числа учитываемых гармоник точность представления s(t) возрастает.

Совокупность всех гармонических составляющих разложения функции в ряд Фурье называется спектром функции.

Наличие отдельных гармонических составляющих спектра и величины их амплитуд можно наглядно показать с помощью спектральной диаграммы (рис. 2.6), у которой горизонтальная ось служит осью частот, а вертикальная – осью амплитуд.

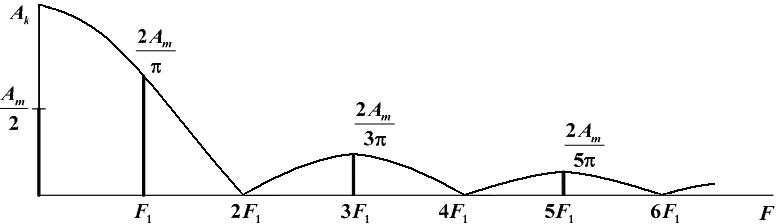
Рис. 2.6. Спектр амплитуд прямоугольных импульсов

В точках оси частот F₁, 3F₁, 5F₁, …, отображаются амплитуды соответствующих гармонических составляющих разложения функции.

На практике спектральные диаграммы называют более кратко – амплитудный спектр, фазовый спектр. Чаще всего интересуются амплитудным спектром (рис. 2.6). По нему можно оценить процентное содержание гармоник, наличие и уровни отдельных гармонических составляющих спектра.