Дифференциальные уравнения второго порядка

Уравнения допускающие понижение порядка

1. Уравнение вида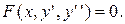

Это уравнение не содержит в явном виде искомой функции у(х). Сделаем замену 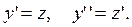Тогда

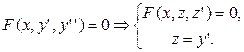
2. Уравнение вида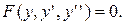

Это уравнение не содержит в явном виде аргумент х, поэтому для его решения предлагается замена 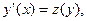т.е. z является функцией от у, а не от х.

Тогда

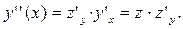
Итак,

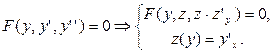
Пример 6.Решить уравнение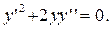

Решение:

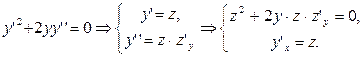
1)

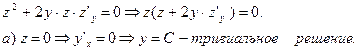
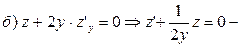линейное однородное уравнение первого порядка, решение которого

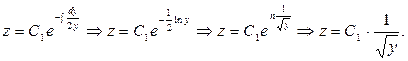
2) 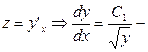уравнение с разделяющимися переменными.

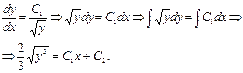
Линейным однородным дифференциальным уравнением второго порядка называется уравнение вида

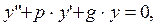
для нахождения линейно независимых решени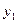й и 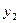уравнения 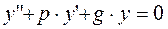надо записать по линейному однородному дифференциальному уравнению второго порядка характеристическое уравнение:

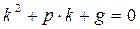
и решить его, т.е. найти корн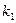и и .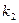

Возможны три случая

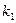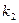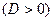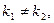1. Корни и характеристического уравнения вещественные и различные ,т.е. тогда общее решение дифференциального уравнения имеет вид:

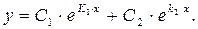
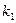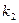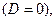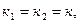2. Корни и характеристического уравнения вещественные и равные друг другу т.е. тогда общее решение дифференциального уравнения имеет вид:

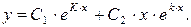
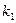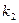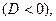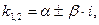3. Корни и характеристического уравнения комплексно–сопряжённые т.е. где 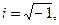тогда общее решение дифференциального уравнения имеет вид:

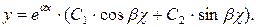
Пример 7.Решить уравнение: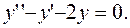

Решение:

Составим и решим характеристическое уравнение:

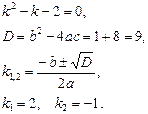
Мы получили действительные и различные корни, следовательно, общее решение данного уравнения находим по формуле:

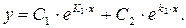
Получим:

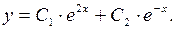
Задания для самостоятельной работы

1.Решить уравнение:

а)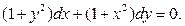

б)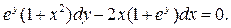

2.Найдите частное решение данного уравнения

а)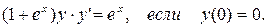

б)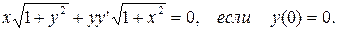

3. Решить уравнение:

а)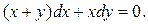

б)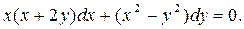

в)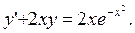

г)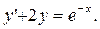

д)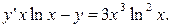

4. Решить уравнение:

1)

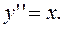
2)

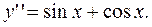
3)

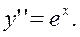
5. Найдите частное решение уравнения 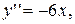удовлетворяющее начальным условиям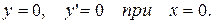

6. Решить уравнение:

1)

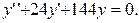
2)

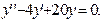
3)

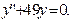
4)

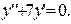
Рекомендуемая литература: 1.2[с. 243-253], 2.2[с. 117-140].

Самостоятельная работа №11

Тема: Разложение в ряд Маклорена предложенных функций

Цель: закрепление умения использования формул Тейлора и Маклорена для разложения функций в степенные ряды.

Время выполнения: 6 часов

Теоретический материал

Числовым рядом называется бесконечная последовательность чисел 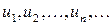, соединенных знаком сложения:

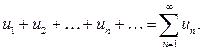
Числа 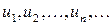называются членами ряда, а член 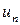- общим или n-м членом ряда.

Среди рядов особое место занимают степенные ряды, членами которых являются степенные функции аргумента х:

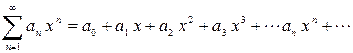
Действительные числа 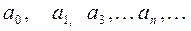называются коэффициентами ряда, х – действительная переменная.

Рассмотренный степенной ряд расположен по степеням х.

Имеют место ряды, расположенные по степеням 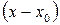, т.е. ряд вида

,

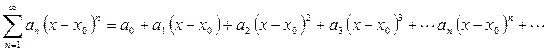где 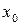- некоторое постоянное число.

Для приложений важно уметь данную функцию f(x) разлагать в степенной ряд, т. е. функцию f(x) представлять в виде суммы степенного ряда.

Для любой функции f(x), определённой в окрестности точки 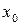и имеющей в ней производные до (n+1)-го порядка включительно, справедлива формула Тейлора:

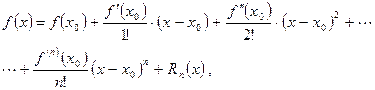
где 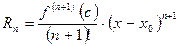, 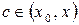- остаточный член в форме Лагранжа.

Число с можно записать в ви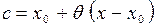де , где .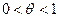

Без остаточного члена имеем – многочлен Тейлора:

.

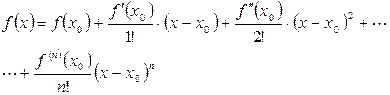Если функция f(x) имеет производные любых порядков (т. е. бесконечно дифференцируема) в окрестности точки 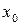и остаточный член 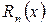стремится к нулю при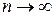 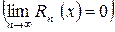, то из формулы Тейлора получается разложение функции f(x) по степеням 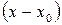, называемое рядом Тейлора:

.

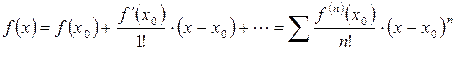Если в ряде Тейлора положить 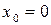, то получим разложение функции по степеням x в так называемый ряд Маклорена:

.

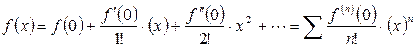Формально ряд Тейлора можно построить для любой бесконечно дифференцируемой функции (это необходимое условие) в окрестности точки 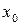. Но отсюда ещё не следует, что он будет сходиться к данной функции f(x); он может оказаться расходящимся или сходиться, но не к функции f(x).

Пример1. Разложить многочлен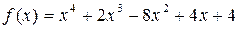

в ряд Тейлора при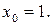

Решение:

Найдём производные данного многочлена:

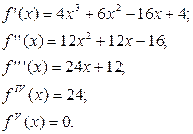
В точке 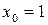имеем:

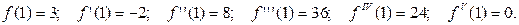
По формуле 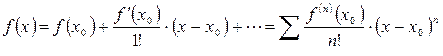получаем:

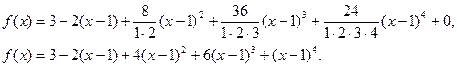
Разложение некоторых элементарных функций в ряд Тейлора (Маклорена)

Для разложения функции f(x) в ряд Маклорена нужно:

1) Найти производные ;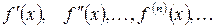

2) Вычислить значения производных в точке ;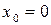

3) Написать ряд

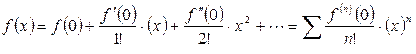
для заданной функции и найти его интервал сходимости;

4) Найти интервал (-R; R), в котором остаточный член ряда Маклорена 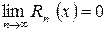. Если такой интервал существует, то в нем функция f(x) и сумма ряда Маклорена совпадают.

Задание для самостоятельной работы

1. Разложить по степеням х элементарные функции:

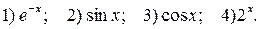
2. Разложить в ряд Маклорена функции:

1)

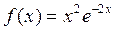
2)

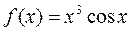
3)

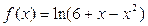
4)

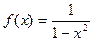
Рекомендуемая литература: 1.2[с. 405-430], 2.2[с. 66-113].

Самостоятельная работа №12

Тема: Действия над комплексными числами

Цель: закрепление навыков выполнения арифметических действий над комплексными числами в алгебраической, тригонометрической и показательной форме.

Время выполнения: 4 часа (для 09.02.03, 09.02.04), 6 часов (для 09.02.01)

Теоретический материал

Комплексным числом называется выражение вида a + ib, где a и b – любые действительные числа, i – специальное число, которое называется мнимой единицей. Для таких выражений понятия равенства и операции сложения и умножения вводятся следующим образом:

1. Два комплексных числа a + ib и c + id называются равными тогда и только тогда, когда a = c и b = d.

2. Суммой двух комплексных чисел a + ib и c + id называется комплексное число a + c + i(b + d).

3. Произведением двух комплексных чисел a + ib и c + id называется комплексное число ac – bd + i(ad + bc).

На комплексные числа можно смотреть как на многочлены с учётом равенства 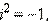то и перемножать эти числа можно как многочлены. В самом деле,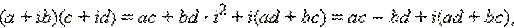

,то есть как раз получается нужная формула.

Геометрической интерпретацией действительных чисел является действительная прямая.

Любому комплексному числу z = x + iy можно поставить в соответствие точку координатной плоскости. На оси абсцисс откладывается действительная часть комплексного числа, а на оси ординат – мнимая часть.

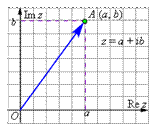
Рис.11. Геометрическая интерпретация комплексного числа (точка).

Любому комплексному числу z = a + ib соответствует вектор 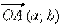и наоборот, каждому вектору 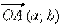соответствует, и притом единственное, число z = a + ib.

Модулем комплексного числа называется длина вектора, соответствующего этому числу:

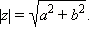
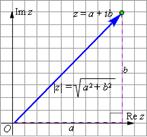
Рис.12. Геометрическая интерпретация комплексного числа (вектор).

Аргументом комплексного числа z = a + ib (z ≠ 0) называется величина угла между положительным направлением действительной оси и вектором 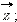величина угла считается положительной, если угол отсчитывается против часовой стрелки, и отрицательным в противном случае.

Угол φ, аргумент комплексного числа, обозначается φ = arg z. Для числа z = 0 аргумент не определён.

Для любых двух чисел z₁ и z₂ существует такое число z, что z₁ + z = z₂. Такое число z называется разностью двух комплексных чисел и обозначается z = z₂ – z₁.

Для любых двух чисел 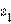и 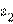существует такое число z, что 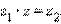Такое число z называется частным двух комплексных чисел и обозначается 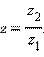Деление на 0 невозможно.

Если число z = a + bi, то число 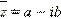называется комплексно- сопряжённым с числом z. Комплексно сопряжённое число обозначается 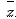Для этого числа справедливы соотношения:

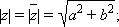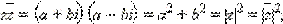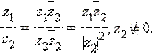Пример 1. Вычислить z₁+ z₂ и z₁z₂, где z₁ = 1 + 2i и z₂ = 2 – i.

Решение:

Выполним действия:

1) Имеем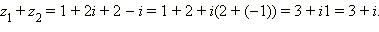

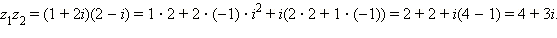
Пример 2.Найдите число, сопряжённое к комплексному числу

(1 + 2i)(3 – 4i).

Решение:

Выполним действия:

(1 + 2i)(3 – 4i)= 3 + 6i – 4i - 8 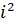=3 + 2i + 8 = 11 + 2i.

Найдем число, сопряжённое к комплексному числу 11 + 2i.

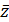=11 - 2i

Имеем .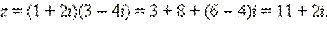

Следовательно,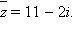

Ответ. 11 – 2i.Пример 3. Вычислите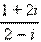

Решение:

Имеем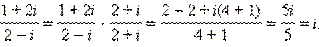

Ответ i.

Та запись комплексного числа, которую мы использовали до сих пор, называется алгебраической формой записи комплексного числа. Часто бывает удобна и другая форма записи комплексного числа. Пусть 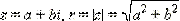и φ = arg z. Тогда по определению аргумента имеем:

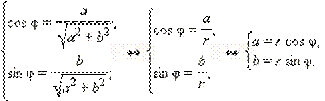Отсюда получается

z = a + bi = r(cos φ + i sin φ).

Такая форма называется тригонометрической формой записи комплексного числа. Как видно, для того, чтобы перейти от алгебраической формы записи комплексного числа к тригонометрической форме, нужно найти его модуль и один из аргументов.

Пример 4.Записать число 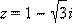в тригонометрической форме.

Решение:

Найдём модуль этого числа: 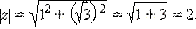Аргумент данного числа находится из системы

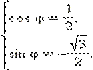Значит, один из аргументов числа 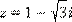равен 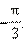Получаем:

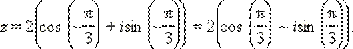Ответ: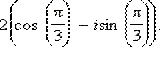

Арифметические действия над комплексными числами, записанными в тригонометрической форме, производятся следующим образом. Пусть z₁ = r₁(cos φ₁ + i sin φ₁) и z₂ = r₂(cos φ₂ + i sin φ₂). Имеем:

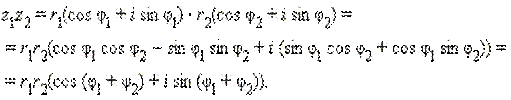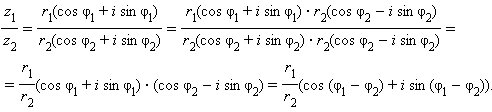Отсюда следует, что для того чтобы перемножить n комплексных чисел, нужно перемножить их модули и сложить аргументы: если φ₁, φ₂, ..., φ_n – аргументы чисел z₁, z₂, ..., z_n, то

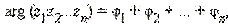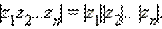В частности, если все эти числа равны между собой, то получим формулу, позволяющую возводить комплексное число в любую натуральную степень.

Первая формула Муавра:

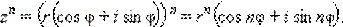Пример 5. Вычислить 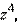если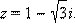

Решение:

Данное число в тригонометрической форме имеет вид 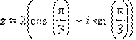По первой формуле Муавра получаем:

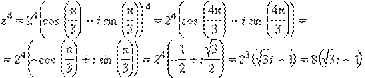Ответ: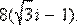

Число z называется корнем степени 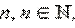из комплексного числа w, если 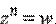Корень степени 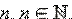обозначается 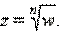. Пусть теперь число w фиксировано. Найдём z из уравнения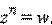

Вторая формула Муавра:

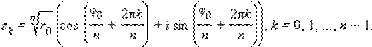Задания для самостоятельной работы

1. Найти числа сопряжённые данным комплексным числам, изобразить их геометрически:

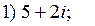
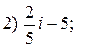
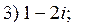
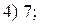
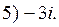
2. Вычислить:

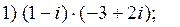
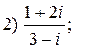
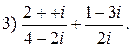
3. Решить уравнения:

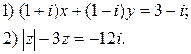
4. Представить в тригонометрической форме числа:

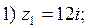
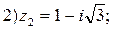
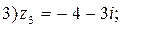
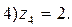
Вычислите: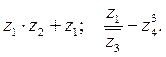

5. Найти значения корня:

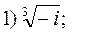
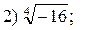
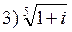
Рекомендуемая литература: 1.2[с. 229-239].

СПИСОК ЛИТЕРАТУРЫ

1. Основная:

1.1 Богомолов, Н.В. Математика [Текст]: учебник для бакалавров / Н.В. Богомолов, П.И.Самойленко. - 5-е изд. - М.: Юрайт, 2014. - 396 с.

1.2 Богомолов, Н.В. Практические занятия по математике [Текст]: учебное пособие для бакалавров / Н.В. Богомолов. - 11-е изд. - М.: Юрайт, 2015. - 495 с.

1.3 Григорьев, В.П. Элементы высшей математики [Текст]: учеб. для студ. учреждений сред. проф. образования / В.П. Григорьев, Ю.А. Дубинский. - 10-е изд. – М.: Академия, 2012. – 320 с.

1.4 Григорьев, С.Г. Математика [Текст]: учебник для студ. сред. проф. учреждений / под ред. В.А. Гусева. – 3-е изд., стер. – М.: Академия, 2012. – 384 с.

2.Дополнительная:

2.1 Данко, П.Е., Высшая математика в упражнениях и задачах. В 2 ч. Ч.1: учеб. пособие для вузов / П.Е.Данко, А.Г. Попов, Т.Я. Кожевникова. – 8-е изд. – М.: ООО «Издательский дом «ОНИКС 21 век»: ООО «Издательство «Мир и Образование», 2014. – 304 с.

2.2 Данко, П.Е. Высшая математика в упражнениях и задачах. В 2 ч. Ч.2: Учеб. пособие для вузов / П.Е.Данко, А.Г. Попов, Т.Я. Кожевникова. – 8-е изд. – М.: ООО «Издательский дом «ОНИКС 21 век»: ООО «Издательство «Мир и Образование»», 2014. – 416 с.

Учебное издание

ЭЛЕМЕНТЫ ВЫСШЕЙ МАТЕМАТИКИ

Методические указания по выполнению самостоятельных работ

Составитель

ПЕТРОВА Татьяна Александровна

В авторской редакции

Подписано в печать . Формат 60х90 1/16. Усл. печ. л. 3,0.

Тираж 35 экз. Заказ № .