Процедура скользящего суммирования

Пусть

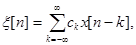(2.58)

где x[n] - нормальный дискретный «белый шум».

Тогда спектральная плотность процесса (2.58) на основе (2.51) имеет вид:

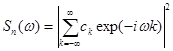(2.59)

Корреляционная функция процесса (2.58) определяется зави­симостью (2.47).

Считая известными значения корреляционной функции К_п(n) в достаточно большом диапазоне –р £ n £ p, можно найти с доста­точной точностью ее преобразование Фурье - спектральную плот­ность S_п(w), а затем разлагая корень из нее в ряд Фурье, найти коэффициенты с_k. Это дает возможность моделировать сам процесс с помощью соотношения:

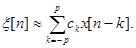(2.60)

Для моделирования начального значения нужно иметь 2р+1 нормальных случайных величин N(0,1), а для последующих - еще одно дополнительное случайное число.

Количество слагаемых в зависимости (2.60) зависит от тре­буемой точности и характеристик процесса и, как правило, не превосходит 5...10.

Нетрудно показать, что для СНСП, имеющего корреляци­онную функцию (2.39) и спектральную плотность, полученную в результате преобразования Фурье:

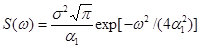(2.61)

коэффициенты определяются зависимостью:

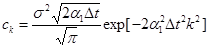. (2.62)

Для моделирования СНСП по рассмотренным алгоритмам необ­ходимо достаточно корректно определить шаг дискретизации (Dt). Для этого необходимо знать:

1. Интервал времени моделирования случайного процесса Т в секундах.

2. Интервал частот, в которых задана спектральная плот­ность - [-В; В] в герцах (ширину частотного спектра).

Тогда необходимое число равноотстоящих выборочных значе­ний последовательности без существенной потери информации оп­ределяется зависимостью:

n³ 2BT, (2.63)

а интервал дискретизации:

Dt = Т/n. (2.64)

Кроме того минимальный интервал времени моделирования и ошибка измерения основных характеристик случайного процесса (МОЖ, корреляционной функции, спектральной плотности) связаны равенством:

Т_min= (Be²)^-1, (2.65)

где e - погрешность измерения характеристик процесса.

Случайный процесс, протекающий в системе, называется мар­ковским, если для любого момента времени t₀ вероятностные ха­рактеристики процесса в будущем зависят только от его состоя­ния в данный момент времени и не зависят от того, когда и как система пришла в это состояние.

Марковские случайные процессы наибольшее применение нахо­дят при исследовании систем массового обслуживания, на которых поступает простейший поток заявок, т.е. стационарный, ординар­ный и не имеющий последействия. При этом хорошо известно, что интервал времени между соседними заявками имеет показа­тельное распределение.

Поэтому моделирование марковского случайного процесса сводится к моделированию моментов времени t_i, характеризующих временную последовательность поступления заявок, т.е. к моде­лированию случайных величин, имеющих показательное распределе­ние.

Порядок выполнения работы.

1. Составить программу в системе Matlab (расширение файла *.m), реализующую заданный метод моделирования случайных величин (функций).

2. Провести моделирование случайных величин и функций с использованием разработанной программы.

3. Построить графики исчерпывающих характеристик случайных величин и реализаций случайной функции.

4. Сделать выводы о полученных результатах.

5. Отчет о лабораторной работе представить в печатном виде с необходимыми иллюстрациями.

Варианты заданий.

№ варианта	Генерирование дискретной СВ	Генерирование непрерывной СВ	Генерирование СНСП
	Отрицательное биномиальное распределение n = 40; p = 0.4	Нормальное распределение 0,15	Рекуррентная процедура mx= 1; sx = 4.5; a= 15; T = 0.8c; n = 5; Dt = 0.02c; N = 60
	Распределение Пуассона λ=700	Логнормальное распределение 0,15	Процедура скользящего суммирования mx= 1; sx = 4.5; a1 = 15; T = 0.8c; n = 5; Dt = 0.02c; p= 4; N=60
	Биномиальное распределение n = 10; p = 0.4	Логнормальное распределение 1,1	Процедура скользящего суммирования mx= -1; sx = 3; a1 = 9; T = 0.1c; n = 5; Dt = 0.05c; p= 5; N=90
	Геометрическое распределение p = 0.5	Гамма-распределение 1,0	Рекуррентная процедура mx= -2; sx = 3; a= 12; T = 0.6c; n = 7; Dt = 0.2c; N = 110
	Распределение Паскаля n = 30; p = 0.2	Равномерное распределение [5,25]	Процедура скользящего суммирования mx= -2; sx = 3; a1 = 13; T = 0.5c; n = 7; Dt = 0.2c; p= 6; N=80
	Отрицательное биномиальное распределение n = 15; p = 0.6	Показательное распределение l=2	Рекуррентная процедура mx= 0; sx = 4; a= 11; T = 0.7c; n = 5; Dt = 0.2c; N = 120
	Биномиальное распределение n = 20; p = 0.3	Равномерное распределение [-2,5]	Рекуррентная процедура mx= 0; sx = 3; a= 10; T = 0.3c; n = 3; Dt = 0.1c; N = 70
	Геометрическое распределение p = 0.4	Показательное распределение l=3	Процедура скользящего суммирования mx= 0; sx = 2; a1 = 10; T = 0.3c; n = 3; Dt = 0.1c; p= 3; N=100
	Распределение Паскаля n = 16; p = 0.6	Распределение Рэлея σ=3	Рекуррентная процедура mx= 1; sx = 4; a= 11; T = 1.4c; n = 4; Dt = 0.2c; N = 80
	Отрицательное биномиальное распределение n = 30; p = 0.5	Распределение Вейбулла -1,5	Процедура скользящего суммирования mx= 1; sx = 5; a1 = 11; T = 2.4c; n = 4; Dt = 0.2c; p= 4; N=90
	Распределение Пуассона λ=200	Нормальное распределение 1,5	Рекуррентная процедура mx= -1; sx = 6; a= 9; T = 1.1c; n = 5; Dt = 0.05c; N = 100
	Биномиальное распределение n = 30; p = 0.4	Логнормальное распределение 1,5	Процедура скользящего суммирования mx= -1; sx = 2; a1 = 9; T = 2.1c; n = 5; Dt = 0.05c; p= 4; N=110
	Геометрическое распределение p = 0.6	Гамма-распределение 1,3	Рекуррентная процедура mx= -1; sx = 4; a= 14; T = 0.5c; n = 7; Dt = 0.2c; N = 80
	Распределение Паскаля n = 40; p = 0.4	Равномерное распределение [2,10]	Процедура скользящего суммирования mx= -2; sx = 4; a1 = 14; T = 1.5c; n = 7; Dt = 0.2c; p= 4; N=90
	Отрицательное биномиальное распределение n = 30; p = 0.5	Показательное распределение l=5	Рекуррентная процедура mx= 0; sx = 5; a= 10; T = 1.5c; n = 5; Dt = 0.2c; N = 70
	Распределение Пуассона λ=2000	Распределение Рэлея σ=2	Процедура скользящего суммирования mx= 0; sx = 4; a1 = 10; T = 1.5c; n = 5; Dt = 0.2c; p= 3; N=120
	Биномиальное распределение n = 40; p = 0.6	Распределение Вейбулла 4,15	Рекуррентная процедура mx= -1; sx = 3; a= 8; T = 2.0c; n = 5; Dt = 0.1c; N = 70
	Геометрическое распределение p = 0.7	Нормальное распределение 5,10	Процедура скользящего суммирования mx= -1; sx = 4; a1 = 8; T = 2.0c; n = 5; Dt = 0.1c; p= 4; N=90
	Распределение Паскаля n = 50; p = 0.8	Логнормальное распределение 4,20	Рекуррентная процедура mx= -1; sx = 5; a= 9; T = 2.1c; n = 4; Dt = 0.2c; N = 90
	Биномиальное распределение n = 10; p = 0.4	Равномерное распределение [-4,5]	Рекуррентная процедура mx= 0; sx = 5; a= 10; T = 0.3c; n = 3; Dt = 0.1c; N = 50
	Геометрическое распределение p = 0.6	Показательное распределение l=2	Процедура скользящего суммирования mx= 0; sx = 5; a1 = 10; T = 0.3c; n = 3; Dt = 0.1c; p= 3; N=50
	Распределение Паскаля n = 10; p = 0.4	Распределение Рэлея σ=2	Рекуррентная процедура mx= 1; sx = 6; a= 11; T = 0.4c; n = 4; Dt = 0.2c; N = 60
	Отрицательное биномиальное распределение n = 10; p = 0.4	Распределение Вейбулла -4,5	Процедура скользящего суммирования mx= 1; sx = 6; a1 = 11; T = 0.4c; n = 4; Dt = 0.2c; p= 4; N=60
	Распределение Пуассона λ=100	Нормальное распределение 1,3	Рекуррентная процедура mx= -1; sx = 4; a= 9; T = 0.1c; n = 5; Dt = 0.05c; N = 80
	Биномиальное распределение n = 20; p = 0.3	Логнормальное распределение 1,3	Процедура скользящего суммирования mx= -1; sx = 4; a1 = 9; T = 0.1c; n = 5; Dt = 0.05c; p= 4; N=80
	Геометрическое распределение p = 0.4	Гамма-распределение 1,3	Рекуррентная процедура mx= -2; sx = 3; a= 14; T = 0.5c; n = 7; Dt = 0.2c; N = 100
	Распределение Паскаля n = 20; p = 0.3	Равномерное распределение [6,20]	Процедура скользящего суммирования mx= -2; sx = 3; a1 = 14; T = 0.5c; n = 7; Dt = 0.2c; p= 4; N=100
	Отрицательное биномиальное распределение n = 20; p = 0.3	Показательное распределение l=3	Рекуррентная процедура mx= 0; sx = 3; a= 10; T = 0.5c; n = 5; Dt = 0.2c; N = 100
	Распределение Пуассона λ=1000	Распределение Рэлея σ=3	Процедура скользящего суммирования mx= 0; sx = 3; a1 = 10; T = 0.5c; n = 5; Dt = 0.2c; p= 3; N=100
	Биномиальное распределение n = 30; p = 0.7	Распределение Вейбулла 6,20	Рекуррентная процедура mx= -3; sx = 3; a= 8; T = 1.0c; n = 5; Dt = 0.1c; N = 50
	Геометрическое распределение p = 0.8	Нормальное распределение 6,20	Процедура скользящего суммирования mx= -3; sx = 3; a1 = 8; T = 1.0c; n = 5; Dt = 0.1c; p= 4; N=50
	Распределение Паскаля n = 30; p = 0.7	Логнормальное распределение 6,20	Рекуррентная процедура mx= -2; sx = 5; a= 9; T = 1.1c; n = 4; Dt = 0.2c; N = 70

ЛИТЕРАТУРА

1. Бендат Дж., Пирсол А. Измерение и анализ случайных про­цессов. - М.: Мир, 1971.

2. Бочаров П.П., Печенкин А.В. Теория массового обслужива­ния. - М.: Из-во РУДН, 1995.

3. Бусленко Н.П., Голенко Д.И., Соболь И.М., Срагович В.Г., Шрейдер Ю.А. Метод статистических испытаний (метод Монте-Кар­ло).-М.: Физматгиз, 1962.

4. Бусленко Н.П. Моделирование сложных систем. - М.: Наука, 1978.

5. Вентцель Е.С. Исследование операций. - М.: Сов. радио, 1972.

6. Вентцель Е.С. Исследование операций. Задачи, принципы, методология. - М.: Гл.ред.физ.мат. лит., 1988.

7. Вентцель Е.С. Теория вероятностей. - М.: Наука, 1969.

8. Гмурман В.Е. Теория вероятностей и математическая ста­тистика. - М.: Высшая школа, 1977.

9. Голенко Д.И. Моделирование и статистический анализ псевдослучайных чисел на ЭВМ.-М.: Наука, 1965.

10. Егоренков Д.Л., Фрадков А.Л., Харламов В.Ю. Основы математического моделирования с примерами на языке MATLAB.-СПБ.: БГТУ, 1994.

11. Ермаков С.М. Метод Монте-Карло и смежные вопросы. - М.: Наука, 1971.

12. Ермаков С.М., Михайлов Г.А. Курс статистического моде­лирования. - М.: Наука, 1976.

13. Железнов И.Г. Сложные технические системы (оценка ха­рактеристик).-М.: Высшая школа, 1984.

14. Калинина В.Н., Панкин В.Ф. Математическая статисти­ка. - М.: Высшая школа, 1994.

15. Леман Э. Теория точечного оценивания. - М.: Наука, 1991.

16. Льюнг Л. Идентификация систем. Теория для пользовате­ля. -М.: Наука, 1991.

17. Полляк Ю.Г. Вероятностное моделирование на ЭВМ.-М.: Сов. радио, 1971.

18. Свешников А.А. Прикладные методы теории случайных функций. - Л.: Судпромгиз, 1961.

19. Соболь И.М. Метод Монте-Карло. - М.: Наука, 1978.

20. Советов Б.Я., Яковлев С.А. Моделирование систем. -М.: Высшая школа,1985.

21. Хастингс И., Пикок Дж. Справочник по статистическим распределениям. - М.: Статистика, 1980.

22. Максимей И.В. Имитационное моделирование на ЭВМ. –М.: Радио и связь, 1988.- 232 с.

23. Цвиркин А.Д. Имитационное моделирование в задачах синтеза структуры сложных систем. –М.: Радио и связь, 1985.- 214 с.