Моделирование случайных процессов

Рассмотрим алгоритмы моделирования стаци­онарного нормального и марковского случайных процессов. Эти процессы имеют широкое распространение в качестве математических моделей различного рода реальных процессов, протекающих в сложных технических системах. Приведем далее некоторые сущест­венные для дальнейшего изложения определения и понятия, приня­тые в рамках корреляционной и спектральной теорий случайных функций.

Случайной функцией называют функцию неслучайного аргумен­та t, которая при каждом фиксированном значении аргумента яв­ляется случайной величиной. Случайную функцию времени называют случайным процессом. Случайную функцию координат точки прост­ранства называют случайным полем. Конкретный вид, принимаемый случайным процессом в результате опыта, называется реализацией (траекторией) случайного процесса. Все полученные реализации случайного процесса составляют ансамбль реализаций. Значения реализаций в конкретные моменты времени (временные сечения) называются мгновенными значениями случайного процесса.

Введем следующие обозначения: Х(t) - случайный процесс; x_i(t) - i-ая реализация процесса X(t); x_i(t_j) - мгновенное значение процесса Х(t), соответствующее i-ой реализации в j-ый момент времени. Совокупность мгновенных значений, соответству­ющих значениям различных реализаций в один и тот же момент времени t_j, назовем j-ой последовательностью процесса Х(t) и обозначим х(t_j). Из сказанного следует, что в качестве аргу­ментов случайного процесса могут выступать время и номер реа­лизации. В связи с этим правомерны два подхода к изучению свойств случайного процесса: первый основан на анализе мно­жества реализаций, второй оперирует множеством последователь­ностей - временных сечений. Наличие или отсутствие зависимости значений вероятностных характеристик случайного процесса от времени или номера реализации определяет такие фундаментальные свойства процесса, как стационарность и эргодичность. Стацио­нарным называется процесс, вероятностные характеристики кото­рого не зависят от времени. Эргодическим называется процесс, вероятностные характеристики которого не зависят от номера ре­ализации.

Случайный процесс называется нормальным (или гауссовским) процессом, если одномерные и двумерные законы распределения любых его сечений нормальны. Исчерпывающими характеристиками нормального случайного процесса является его математическое ожидание и корреляционная функция. У стационарного нормального случайного процесса МОЖ постоянно, а корреляционная функция зависит только от разности моментов времени, для которых взяты ординаты случайного процесса ( 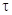=t₂-t₁). Для стационарного слу­чайного процесса при достаточно большом 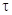отклонение ординаты случайного процесса Х(t₂) от ее математического ожидания m_x в момент времени t₂ становится практически независимым от значе­ния этого отклонения в момент времени t₁. В этом случае корре­ляционная функция К(t), дающая значение момента связи между Х(t₂) и Х(t₁), при 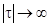будет стремится к нулю. Поэтому К( 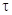) может или монотонно убывать, как это изображено на рис.2.2, или иметь вид, представленный на рис.2.3. Функция ви­да (рис.2.2.), как правило, аппроксимируется выражениями:

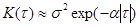(2.38)

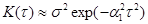, (2.39)

а функция вида (рис.2.3.) - выражениями:

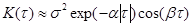(2.40)

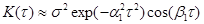. (2.41)

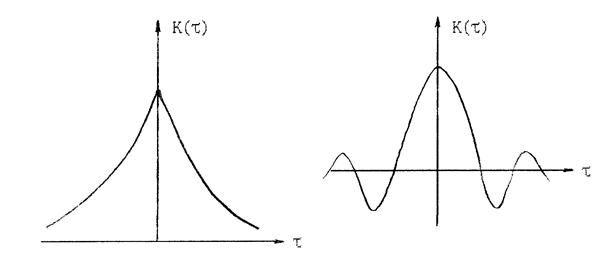
Рис.2.2. Рис.2.3.

Устойчивость стационарного случайного процесса во времени позволяет заменить аргумент - время - некоторой вспомогатель­ной переменной, которая во многих приложениях имеет размер­ность частоты. Такая замена позволяет значительно упростить выкладки и добиться большей наглядности результатов. Получае­мая функция (S( 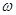)) называется спектральной плотностью стацио­нарного случайного процесса и связана с корреляционной функци­ей взаимно обратными преобразованиями Фурье:

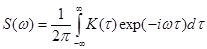(2.42)

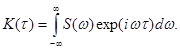(2.43)

Существуют и другие нормировки спектральной плотности, например:

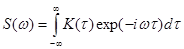(2.44)

На основе преобразований Фурье нетрудно получить, напри­мер, для случайного процесса с K(t) вида (2.38):

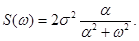(2.45)

Стационарный случайный процесс, спектральная плотность которого постоянна (S(w)=S=const), называется стационарным бе­лым шумом. Корреляционная функция стационарного белого шума равна нулю при всех 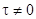, что означает некоррелированность лю­бых двух его сечений.

Задача моделирования стационарного нормального случайного процесса (СНСП) может быть сформулирована как задача нахожде­ния алгоритма, позволяющего получить на ЭВМ дискретные реали­зации этого процесса. Процесс X(t) заменяется с заданной точ­ностью соответствующим процессом X(nDt) с дискретным временем t_n= nDt (Dt- шаг дискретизации процесса, n- целочисленный ар­гумент). В результате случайному процессу x(t) будут поставле­ны в соответствие случайные последовательности:

x_k[n]=x_k(nDt), (2.46)

где k - номер реализации.

Очевидно, что произвольный член случайной последователь­ности x(nDt) можно рассматривать как случайную функцию его но­мера, т.е. целочисленного аргумента n и, таким образом, исклю­чить из рассмотрения Dt, что и учтено при записи (2.46). Кроме того, чтобы отличить целочисленный аргумент от непрерывноизме­няющегося, его заключают в квадратные скобки.

Часто случайные последовательности называют дискретным случайным процессом или временным рядом.

Известно, что добавление к случайной функции неслучайной величины не изменяет значения корреляционной функции. Поэтому на практике очень часто моделируют центрированные случайные процессы (МОЖ равно нулю), от которых можно всегда перейти к реальному путем добавления МОЖ к членам случайной последова­тельности, имитирующей случайный процесс.

Для случайных последовательностей корреляционная функция и спектральная плотность вычисляются по зависимостям:

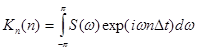(2.47)

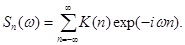(2.48)

Сведение случайного процесса к случайной последователь­ности по сути означает его замену многомерным вектором. Поэто­му рассмотренный метод моделирования случайных векторов, вооб­ще говоря, пригоден для моделирования случайных процессов, за­данных на конечном интервале времени. Однако для стационарных нормальных случайных процессов существуют более эффективные методы построения моделирующих алгоритмов. Рассмотрим два спо­соба, получившие наибольшее применение на практике.

Рекуррентная процедура

Данный способ основан на представлении спектральной плот­ности в виде дробно-рациональной функции, т.е. отношением двух полиномов:

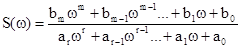(2.49)

Если m < r, a₀ =1 и коэффициенты b_m по модулю меньше еди­ницы, то справедливо разностное уравнение:

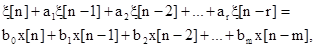(2.50)

где x[n] - стационарная последовательность независимых стандартных нормальных случайных величин (нормальный дискрет­ный белый шум);

x[n] - стационарная последовательность нормальных случайных величин, коррелированная по заданному закону.

Применение зависимости (2.50) с точки зрения исследования линейных стационарных систем означает, что искомая последова­тельность x[n] на выходе системы получается, если на ее вход подать нормальный дискретный белый шум, у которого спектраль­ная плотность постоянна и равна 1. Тогда, как известно, спектральная плотность выходной последовательности определяет­ся по зависимости:

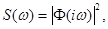(2.51)

где Ф(iw) - передаточная функция системы, которую можно представить в виде (2.49), если перейти к комплексной перемен­ной.

Из (2.50) следует:

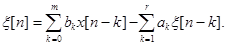(2.52)

Построим моделирующий алгоритм для СНСП, имеющего корре­ляционную функцию (2.38) и спектральную плотность (2.45):

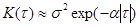
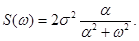
Для последовательности x[n] данные выражения примут вид:

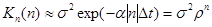
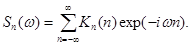
где r= exp(-aDt).

Перепишем S_п(w) в виде:

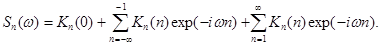
Полагая в первой сумме -n=p, а во второй n=p и принимая во внимание K(-p)=K(p), перепишем полученную формулу в виде:

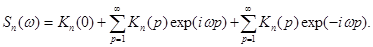(2.53)

Подставляя сюда выражение корреляционной функции, нетруд­но убедится в том, что обе суммы представляют собой геометри­ческие прогрессии. Суммируя их, получим следующее выражение спектральной плотности рассматриваемой стационарной случайной последовательности:

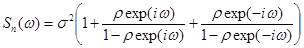(2.54)

В результате элементарных преобразований данной зависи­мости можно придать вид:

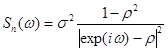(2.55)

Сравнивая полученное выражение с (2.49) и учитывая (2.51), нетрудно получить:

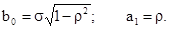(2.56)

На основании (2.52) моделирующий алгоритм примет вид:

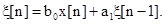(2.57)

В качестве начального значения x[0] можно принять матема­тическое ожидание.