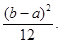Случайные величины и случайные функции

Лабораторная работа № 3

по дисциплине «Математические основы теории систем»

Случайные величины и случайные функции

Цель работы: моделирование случайных величин и случайных процессов на основе метода статистических испытаний.

Задание. Смоделировать случайные величины и случайные процессы в соответствии с заданным вариантом.

Общие положения

Сущность метода статистических испытаний (МСИ) заключается в многократной имитации изучае­мых процессов и явлений с последующей статистической обработ­кой полученных данных. Узловым моментом в методе выступает мо­делирование различного рода воздействий, которое носит харак­тер имитации случайных событий, величин и процессов.

Можно выделить основные этапы применения (составляющие) МСИ для исследования сложных систем:

1. Определение случайных параметров и процессов функциони­рования системы, исходя из целей исследования. На основании опыта или имеющейся априорной информации оценка характеристик случайности (определение вероятности событий, выбор законов распределения и оценка их параметров, определение и оценка корреляционных функций и т.д.).

2. Разработка алгоритмов моделирования случайных событий, величин и процессов и оценка их качества (проведение тестовых проверок).

3. Разработка моделирующего алгоритма, имитирующего пове­дение и взаимодействие элементов системы с учетом случайных входных воздействий и воздействий внешней среды, и реализация этого алгоритма с использованием программно-технических средс­тв ЭВМ.

4. Определение необходимого числа статистических испытаний (прогонов, реализаций), исходя из требуемых характеристик точ­ности и надежности выходных параметров системы в статистическом смысле.

5. Проведение вычислительного эксперимента и статистичес­кая обработка полученных данных.

Теоретической основой МСИ являются предельные теоремы те­ории вероятностей. Множества случайных явлений (событий, вели­чин) подчиняются определенным закономерностям, позволяющим не только прогнозировать их поведение, но и количественно оцени­вать некоторые средние их характеристики, проявляющие опреде­ленную устойчивость. Характерные закономерности наблюдаются также в распределениях случайных величин, которые образуются при сложении множества воздействий. Выражением этих закономер­ностей и устойчивости средних показателей являются так называ­емые предельные теоремы теории вероятностей. Принципиальное значение предельных теорем состоит в том, что они гарантируют высокое качество статистических оценок при весьма большом чис­ле испытаний (реализаций). При практическом использовании МСИ, как правило, достаточным бывает использование закона больших чисел в виде теорем Бернулли и Чебышева, а также центральной предельной теоремы:

Теорема Бернулли. Если проводится N независимых испыта­ний, в каждом из которых некоторое событие А осуществляется с вероятностью р, то относительная частота (частость) появления события m/N при N 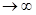сходится по вероятности к р, т.е. при любом 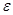> 0

lim P{|m/N-p| 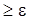} =0, (1.1)

N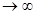

где m- число положительных исходов испытания.

Теорема Чебышева. Если в N независимых испытаниях наблю­даются значения x_1,…,x_n случайной величины Х, то при N 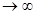среднее арифметическое значений случайной величины сходится по вероятности к P ее математическому ожиданию а, т.е. при любом e>0

lim Р{|(1/N) 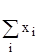-a| 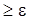}=0. (1.2)

N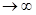

Центральная предельная теорема (в одной из формулировок Ляпунова). Если случайная величина Х имеет конечные математи­ческое ожидание М[Х] и дисперсию D[X], то распределение сред­него арифметического 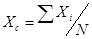, вычисленного по наблюдавшимся значениям случайной величины в N независимых испытаниях, про­веденных в одинаковых условиях, при N 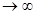приближается к нор­мальному с МОЖ М[Х] и дисперсией D[X]/N.

Таким образом, метод статистических испытаний основан на самых общих теоремах теории вероятностей и не содержит в своей принципиальной сущности никаких ограничений. Применяется он как для исследования стохастических систем, так и для решения детерминированных задач.

Равномерное распределение

Для разработки алгоритмов моделирования случайных собы­тий, величин и процессов фундаментальную роль играет стандарт­ное равномерное распределение R(0,1). Для имитации на ЭВМ случайных явлений самой различной природы достаточно получить на ЭВМ последовательность значений случай­ной величины, равномернораспределенной на отрезке [0,1].

Непрерывная СВ Х имеет равномерное распределение на от­резке [a,b], если ее функция плотности имеет вид:

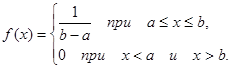
Функция распределения СВ Х имеет вид:

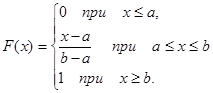(1.16)

Математическое ожидание и дисперсия случайной величины Х соответственно равны:

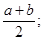М[X]= D[X]=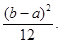

Рекуррентная процедура

Данный способ основан на представлении спектральной плот­ности в виде дробно-рациональной функции, т.е. отношением двух полиномов:

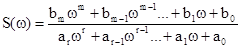(2.49)

Если m < r, a₀ =1 и коэффициенты b_m по модулю меньше еди­ницы, то справедливо разностное уравнение:

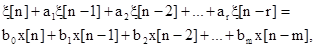(2.50)

где x[n] - стационарная последовательность независимых стандартных нормальных случайных величин (нормальный дискрет­ный белый шум);

x[n] - стационарная последовательность нормальных случайных величин, коррелированная по заданному закону.

Применение зависимости (2.50) с точки зрения исследования линейных стационарных систем означает, что искомая последова­тельность x[n] на выходе системы получается, если на ее вход подать нормальный дискретный белый шум, у которого спектраль­ная плотность постоянна и равна 1. Тогда, как известно, спектральная плотность выходной последовательности определяет­ся по зависимости:

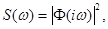(2.51)

где Ф(iw) - передаточная функция системы, которую можно представить в виде (2.49), если перейти к комплексной перемен­ной.

Из (2.50) следует:

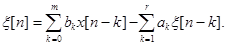(2.52)

Построим моделирующий алгоритм для СНСП, имеющего корре­ляционную функцию (2.38) и спектральную плотность (2.45):

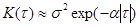
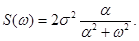
Для последовательности x[n] данные выражения примут вид:

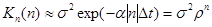
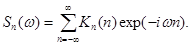
где r= exp(-aDt).

Перепишем S_п(w) в виде:

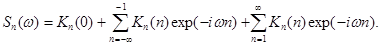
Полагая в первой сумме -n=p, а во второй n=p и принимая во внимание K(-p)=K(p), перепишем полученную формулу в виде:

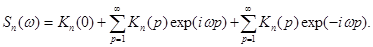(2.53)

Подставляя сюда выражение корреляционной функции, нетруд­но убедится в том, что обе суммы представляют собой геометри­ческие прогрессии. Суммируя их, получим следующее выражение спектральной плотности рассматриваемой стационарной случайной последовательности:

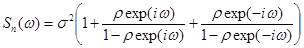(2.54)

В результате элементарных преобразований данной зависи­мости можно придать вид:

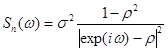(2.55)

Сравнивая полученное выражение с (2.49) и учитывая (2.51), нетрудно получить:

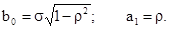(2.56)

На основании (2.52) моделирующий алгоритм примет вид:

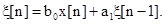(2.57)

В качестве начального значения x[0] можно принять матема­тическое ожидание.

Порядок выполнения работы.

1. Составить программу в системе Matlab (расширение файла *.m), реализующую заданный метод моделирования случайных величин (функций).

2. Провести моделирование случайных величин и функций с использованием разработанной программы.

3. Построить графики исчерпывающих характеристик случайных величин и реализаций случайной функции.

4. Сделать выводы о полученных результатах.

5. Отчет о лабораторной работе представить в печатном виде с необходимыми иллюстрациями.

Варианты заданий.

№ варианта	Генерирование дискретной СВ	Генерирование непрерывной СВ	Генерирование СНСП
	Отрицательное биномиальное распределение n = 40; p = 0.4	Нормальное распределение 0,15	Рекуррентная процедура mx= 1; sx = 4.5; a= 15; T = 0.8c; n = 5; Dt = 0.02c; N = 60
	Распределение Пуассона λ=700	Логнормальное распределение 0,15	Процедура скользящего суммирования mx= 1; sx = 4.5; a1 = 15; T = 0.8c; n = 5; Dt = 0.02c; p= 4; N=60
	Биномиальное распределение n = 10; p = 0.4	Логнормальное распределение 1,1	Процедура скользящего суммирования mx= -1; sx = 3; a1 = 9; T = 0.1c; n = 5; Dt = 0.05c; p= 5; N=90
	Геометрическое распределение p = 0.5	Гамма-распределение 1,0	Рекуррентная процедура mx= -2; sx = 3; a= 12; T = 0.6c; n = 7; Dt = 0.2c; N = 110
	Распределение Паскаля n = 30; p = 0.2	Равномерное распределение [5,25]	Процедура скользящего суммирования mx= -2; sx = 3; a1 = 13; T = 0.5c; n = 7; Dt = 0.2c; p= 6; N=80
	Отрицательное биномиальное распределение n = 15; p = 0.6	Показательное распределение l=2	Рекуррентная процедура mx= 0; sx = 4; a= 11; T = 0.7c; n = 5; Dt = 0.2c; N = 120
	Биномиальное распределение n = 20; p = 0.3	Равномерное распределение [-2,5]	Рекуррентная процедура mx= 0; sx = 3; a= 10; T = 0.3c; n = 3; Dt = 0.1c; N = 70
	Геометрическое распределение p = 0.4	Показательное распределение l=3	Процедура скользящего суммирования mx= 0; sx = 2; a1 = 10; T = 0.3c; n = 3; Dt = 0.1c; p= 3; N=100
	Распределение Паскаля n = 16; p = 0.6	Распределение Рэлея σ=3	Рекуррентная процедура mx= 1; sx = 4; a= 11; T = 1.4c; n = 4; Dt = 0.2c; N = 80
	Отрицательное биномиальное распределение n = 30; p = 0.5	Распределение Вейбулла -1,5	Процедура скользящего суммирования mx= 1; sx = 5; a1 = 11; T = 2.4c; n = 4; Dt = 0.2c; p= 4; N=90
	Распределение Пуассона λ=200	Нормальное распределение 1,5	Рекуррентная процедура mx= -1; sx = 6; a= 9; T = 1.1c; n = 5; Dt = 0.05c; N = 100
	Биномиальное распределение n = 30; p = 0.4	Логнормальное распределение 1,5	Процедура скользящего суммирования mx= -1; sx = 2; a1 = 9; T = 2.1c; n = 5; Dt = 0.05c; p= 4; N=110
	Геометрическое распределение p = 0.6	Гамма-распределение 1,3	Рекуррентная процедура mx= -1; sx = 4; a= 14; T = 0.5c; n = 7; Dt = 0.2c; N = 80
	Распределение Паскаля n = 40; p = 0.4	Равномерное распределение [2,10]	Процедура скользящего суммирования mx= -2; sx = 4; a1 = 14; T = 1.5c; n = 7; Dt = 0.2c; p= 4; N=90
	Отрицательное биномиальное распределение n = 30; p = 0.5	Показательное распределение l=5	Рекуррентная процедура mx= 0; sx = 5; a= 10; T = 1.5c; n = 5; Dt = 0.2c; N = 70
	Распределение Пуассона λ=2000	Распределение Рэлея σ=2	Процедура скользящего суммирования mx= 0; sx = 4; a1 = 10; T = 1.5c; n = 5; Dt = 0.2c; p= 3; N=120
	Биномиальное распределение n = 40; p = 0.6	Распределение Вейбулла 4,15	Рекуррентная процедура mx= -1; sx = 3; a= 8; T = 2.0c; n = 5; Dt = 0.1c; N = 70
	Геометрическое распределение p = 0.7	Нормальное распределение 5,10	Процедура скользящего суммирования mx= -1; sx = 4; a1 = 8; T = 2.0c; n = 5; Dt = 0.1c; p= 4; N=90
	Распределение Паскаля n = 50; p = 0.8	Логнормальное распределение 4,20	Рекуррентная процедура mx= -1; sx = 5; a= 9; T = 2.1c; n = 4; Dt = 0.2c; N = 90
	Биномиальное распределение n = 10; p = 0.4	Равномерное распределение [-4,5]	Рекуррентная процедура mx= 0; sx = 5; a= 10; T = 0.3c; n = 3; Dt = 0.1c; N = 50
	Геометрическое распределение p = 0.6	Показательное распределение l=2	Процедура скользящего суммирования mx= 0; sx = 5; a1 = 10; T = 0.3c; n = 3; Dt = 0.1c; p= 3; N=50
	Распределение Паскаля n = 10; p = 0.4	Распределение Рэлея σ=2	Рекуррентная процедура mx= 1; sx = 6; a= 11; T = 0.4c; n = 4; Dt = 0.2c; N = 60
	Отрицательное биномиальное распределение n = 10; p = 0.4	Распределение Вейбулла -4,5	Процедура скользящего суммирования mx= 1; sx = 6; a1 = 11; T = 0.4c; n = 4; Dt = 0.2c; p= 4; N=60
	Распределение Пуассона λ=100	Нормальное распределение 1,3	Рекуррентная процедура mx= -1; sx = 4; a= 9; T = 0.1c; n = 5; Dt = 0.05c; N = 80
	Биномиальное распределение n = 20; p = 0.3	Логнормальное распределение 1,3	Процедура скользящего суммирования mx= -1; sx = 4; a1 = 9; T = 0.1c; n = 5; Dt = 0.05c; p= 4; N=80
	Геометрическое распределение p = 0.4	Гамма-распределение 1,3	Рекуррентная процедура mx= -2; sx = 3; a= 14; T = 0.5c; n = 7; Dt = 0.2c; N = 100
	Распределение Паскаля n = 20; p = 0.3	Равномерное распределение [6,20]	Процедура скользящего суммирования mx= -2; sx = 3; a1 = 14; T = 0.5c; n = 7; Dt = 0.2c; p= 4; N=100
	Отрицательное биномиальное распределение n = 20; p = 0.3	Показательное распределение l=3	Рекуррентная процедура mx= 0; sx = 3; a= 10; T = 0.5c; n = 5; Dt = 0.2c; N = 100
	Распределение Пуассона λ=1000	Распределение Рэлея σ=3	Процедура скользящего суммирования mx= 0; sx = 3; a1 = 10; T = 0.5c; n = 5; Dt = 0.2c; p= 3; N=100
	Биномиальное распределение n = 30; p = 0.7	Распределение Вейбулла 6,20	Рекуррентная процедура mx= -3; sx = 3; a= 8; T = 1.0c; n = 5; Dt = 0.1c; N = 50
	Геометрическое распределение p = 0.8	Нормальное распределение 6,20	Процедура скользящего суммирования mx= -3; sx = 3; a1 = 8; T = 1.0c; n = 5; Dt = 0.1c; p= 4; N=50
	Распределение Паскаля n = 30; p = 0.7	Логнормальное распределение 6,20	Рекуррентная процедура mx= -2; sx = 5; a= 9; T = 1.1c; n = 4; Dt = 0.2c; N = 70

ЛИТЕРАТУРА

1. Бендат Дж., Пирсол А. Измерение и анализ случайных про­цессов. - М.: Мир, 1971.

2. Бочаров П.П., Печенкин А.В. Теория массового обслужива­ния. - М.: Из-во РУДН, 1995.

3. Бусленко Н.П., Голенко Д.И., Соболь И.М., Срагович В.Г., Шрейдер Ю.А. Метод статистических испытаний (метод Монте-Кар­ло).-М.: Физматгиз, 1962.

4. Бусленко Н.П. Моделирование сложных систем. - М.: Наука, 1978.

5. Вентцель Е.С. Исследование операций. - М.: Сов. радио, 1972.

6. Вентцель Е.С. Исследование операций. Задачи, принципы, методология. - М.: Гл.ред.физ.мат. лит., 1988.

7. Вентцель Е.С. Теория вероятностей. - М.: Наука, 1969.

8. Гмурман В.Е. Теория вероятностей и математическая ста­тистика. - М.: Высшая школа, 1977.

9. Голенко Д.И. Моделирование и статистический анализ псевдослучайных чисел на ЭВМ.-М.: Наука, 1965.

10. Егоренков Д.Л., Фрадков А.Л., Харламов В.Ю. Основы математического моделирования с примерами на языке MATLAB.-СПБ.: БГТУ, 1994.

11. Ермаков С.М. Метод Монте-Карло и смежные вопросы. - М.: Наука, 1971.

12. Ермаков С.М., Михайлов Г.А. Курс статистического моде­лирования. - М.: Наука, 1976.

13. Железнов И.Г. Сложные технические системы (оценка ха­рактеристик).-М.: Высшая школа, 1984.

14. Калинина В.Н., Панкин В.Ф. Математическая статисти­ка. - М.: Высшая школа, 1994.

15. Леман Э. Теория точечного оценивания. - М.: Наука, 1991.

16. Льюнг Л. Идентификация систем. Теория для пользовате­ля. -М.: Наука, 1991.

17. Полляк Ю.Г. Вероятностное моделирование на ЭВМ.-М.: Сов. радио, 1971.

18. Свешников А.А. Прикладные методы теории случайных функций. - Л.: Судпромгиз, 1961.

19. Соболь И.М. Метод Монте-Карло. - М.: Наука, 1978.

20. Советов Б.Я., Яковлев С.А. Моделирование систем. -М.: Высшая школа,1985.

21. Хастингс И., Пикок Дж. Справочник по статистическим распределениям. - М.: Статистика, 1980.

22. Максимей И.В. Имитационное моделирование на ЭВМ. –М.: Радио и связь, 1988.- 232 с.

23. Цвиркин А.Д. Имитационное моделирование в задачах синтеза структуры сложных систем. –М.: Радио и связь, 1985.- 214 с.

Лабораторная работа № 3

по дисциплине «Математические основы теории систем»

Случайные величины и случайные функции

Цель работы: моделирование случайных величин и случайных процессов на основе метода статистических испытаний.

Задание. Смоделировать случайные величины и случайные процессы в соответствии с заданным вариантом.

Общие положения

Сущность метода статистических испытаний (МСИ) заключается в многократной имитации изучае­мых процессов и явлений с последующей статистической обработ­кой полученных данных. Узловым моментом в методе выступает мо­делирование различного рода воздействий, которое носит харак­тер имитации случайных событий, величин и процессов.

Можно выделить основные этапы применения (составляющие) МСИ для исследования сложных систем:

1. Определение случайных параметров и процессов функциони­рования системы, исходя из целей исследования. На основании опыта или имеющейся априорной информации оценка характеристик случайности (определение вероятности событий, выбор законов распределения и оценка их параметров, определение и оценка корреляционных функций и т.д.).

2. Разработка алгоритмов моделирования случайных событий, величин и процессов и оценка их качества (проведение тестовых проверок).

3. Разработка моделирующего алгоритма, имитирующего пове­дение и взаимодействие элементов системы с учетом случайных входных воздействий и воздействий внешней среды, и реализация этого алгоритма с использованием программно-технических средс­тв ЭВМ.

4. Определение необходимого числа статистических испытаний (прогонов, реализаций), исходя из требуемых характеристик точ­ности и надежности выходных параметров системы в статистическом смысле.

5. Проведение вычислительного эксперимента и статистичес­кая обработка полученных данных.

Теоретической основой МСИ являются предельные теоремы те­ории вероятностей. Множества случайных явлений (событий, вели­чин) подчиняются определенным закономерностям, позволяющим не только прогнозировать их поведение, но и количественно оцени­вать некоторые средние их характеристики, проявляющие опреде­ленную устойчивость. Характерные закономерности наблюдаются также в распределениях случайных величин, которые образуются при сложении множества воздействий. Выражением этих закономер­ностей и устойчивости средних показателей являются так называ­емые предельные теоремы теории вероятностей. Принципиальное значение предельных теорем состоит в том, что они гарантируют высокое качество статистических оценок при весьма большом чис­ле испытаний (реализаций). При практическом использовании МСИ, как правило, достаточным бывает использование закона больших чисел в виде теорем Бернулли и Чебышева, а также центральной предельной теоремы:

Теорема Бернулли. Если проводится N независимых испыта­ний, в каждом из которых некоторое событие А осуществляется с вероятностью р, то относительная частота (частость) появления события m/N при N 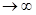сходится по вероятности к р, т.е. при любом 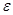> 0

lim P{|m/N-p| 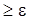} =0, (1.1)

N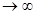

где m- число положительных исходов испытания.

Теорема Чебышева. Если в N независимых испытаниях наблю­даются значения x_1,…,x_n случайной величины Х, то при N 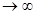среднее арифметическое значений случайной величины сходится по вероятности к P ее математическому ожиданию а, т.е. при любом e>0

lim Р{|(1/N) 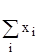-a| 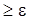}=0. (1.2)

N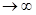

Центральная предельная теорема (в одной из формулировок Ляпунова). Если случайная величина Х имеет конечные математи­ческое ожидание М[Х] и дисперсию D[X], то распределение сред­него арифметического 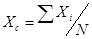, вычисленного по наблюдавшимся значениям случайной величины в N независимых испытаниях, про­веденных в одинаковых условиях, при N 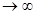приближается к нор­мальному с МОЖ М[Х] и дисперсией D[X]/N.

Таким образом, метод статистических испытаний основан на самых общих теоремах теории вероятностей и не содержит в своей принципиальной сущности никаких ограничений. Применяется он как для исследования стохастических систем, так и для решения детерминированных задач.

Равномерное распределение

Для разработки алгоритмов моделирования случайных собы­тий, величин и процессов фундаментальную роль играет стандарт­ное равномерное распределение R(0,1). Для имитации на ЭВМ случайных явлений самой различной природы достаточно получить на ЭВМ последовательность значений случай­ной величины, равномернораспределенной на отрезке [0,1].

Непрерывная СВ Х имеет равномерное распределение на от­резке [a,b], если ее функция плотности имеет вид:

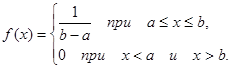
Функция распределения СВ Х имеет вид:

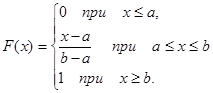(1.16)

Математическое ожидание и дисперсия случайной величины Х соответственно равны:

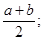М[X]= D[X]=