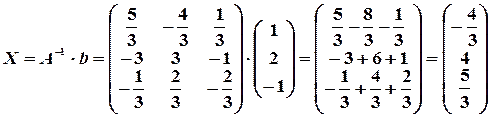Свойства определителя матрицы.

1. Определитель не меняется при транспонировании.

2. Если в определителе переставить две строки, определитель поменяет знак.

3. Определитель, содержащий две одинаковые строки, равен нулю.

4. Определитель, содержащий две пропорциональные строки, равен нулю.

5. Если все элементы строки определителя представлены в виде суммы двух слагаемых , то определитель равен сумме определителей, у которых все строки, кроме 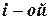, - такие же, как в заданном определителе, а 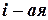строка в одном из слагаемых состоит из элементов 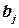, в другом - из элементов .

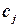Замечание. Все свойства остаются справедливыми, если вместо строк взять столбцы.

Миноры и алгебраические дополнения

Обозначим через 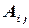матрицу, которая остается при вычеркивании из матрицы 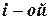строки и 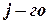столбца. Тогда 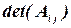называется минором элемента 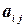. Величина 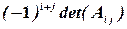называется алгебраическим дополнением элемента .

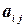Разложение определителя матрицы по элементам строки или столбца.

Теорема. Определитель каждой матрицы равен сумме произведений элементов любой ее строки (столбца) на их алгебраические дополнения, т. е. при разложении по элементам 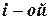строки

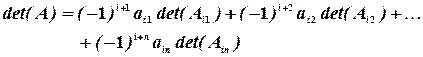
Для вычисления значений определителей матриц второго порядка пользуются формулой:

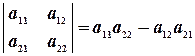
Для вычисления значений определителей матриц третьего порядка можно воспользоваться формулой разложения определителя по первой строке:

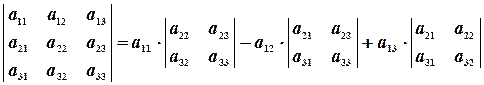
Пример 7.Не вычисляя определителя 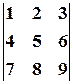, показать, что он равен нулю.

Решение. Вычтем из второй строки первую, получим определитель

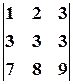, равный исходному. Если из третьей строки также вычесть первую, то получится определитель 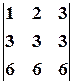, в котором две строки пропорциональны. Такой определитель равен нулю.

Пример 8.Вычислить определитель 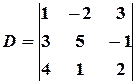, разложив его по элементам второго столбца.

Решение. Разложим определитель по элементам второго столбца:

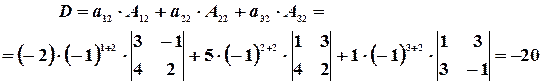
Ранг матрицы

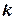Рассмотрим прямоугольную матрицу . Если в этой матрице выделить произвольно строк и столбцов, то элементы, стоящие на пересечении выделенных строк и столбцов, образуют квадратную матрицу 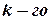порядка. Определитель этой матрицы называется минором k-го порядкаматрицы . Очевидно, что матрица обладает минорами любого порядка от 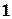до наименьшего из чисел 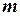и 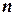. Некоторые среди них будут равны нулю. Среди всех отличных от нуля миноров матрицы найдется, по крайней мере, один минор, порядок которого будет наибольшим. Наибольший из порядков миноров данной матрицы, отличных от нуля, называется рангом матрицы. Если ранг матрицы равен 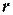, то это означает, что в матрице имеется отличный от нуля минор порядка 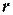, но всякий минор порядка, большего чем 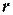, равен нулю. Ранг матрицы обозначается через . 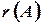Очевидно, что выполняется соотношение

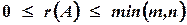
Ранг матрицы находится либо методом окаймления миноров, либо методом элементарных преобразований. При вычислении ранга матрицы первым способом следует переходить от миноров низших порядков к минорам более высокого порядка. Если уже найден минор 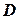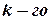порядка матрицы , отличный от нуля, то требуют вычисления лишь миноры 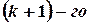порядка, окаймляющие минор 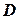, т.е. содержащие его в качестве минора. Если все они равны нулю, то ранг матрицы равен .

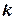Элементарными называются следующие преобразования матрицы:

1) перестановка двух любых строк (или столбцов),

2) умножение строки (или столбца) на отличное от нуля число,

3) прибавление к одной строке (или столбцу) другой строки (или столбца), умноженной на некоторое число.

Две матрицы называются эквивалентными, если одна из них получается из другой с помощью конечного множества элементарных преобразований.

Эквивалентные матрицы не являются, вообще говоря, равными, но их ранги равны. Если матрицы и 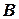эквивалентны, то это записывается так: .

Канонической матрицей называется матрица, у которой в начале главной диагонали стоят подряд несколько единиц (число которых может равняться нулю), а все остальные элементы равны нулю, например,

.

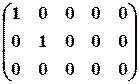При помощи элементарных преобразований строк и столбцов любую матрицу можно привести к канонической. Ранг канонической матрицы равен числу единиц на ее главной диагонали.

Пример 11. Найти методом окаймления миноров ранг матрицы

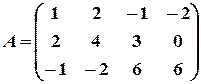
Решение. Начинаем с миноров 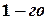порядка, (т.е. с элементов матрицы ). Выберем, например, минор (элемент) 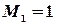, расположенный в первой строке и первом столбце. Окаймляя при помощи второй строки и третьего столбца, получаем минор 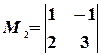, отличный от нуля. Переходим теперь к минорам 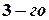порядка, окаймляющим 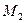. Их всего два (можно добавить второй столбец или четвертый). Вычисляем их:

, .

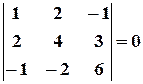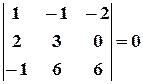Таким образом, все окаймляющие миноры третьего порядка оказались равными нулю. Ранг матрицы равен двум.

Пример 12. Найти ранг матрицы

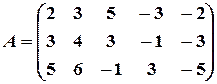
и привести ее к каноническому виду.

Решение. Из второй строки вычтем первую и переставим эти строки:

.

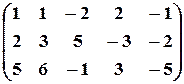Теперь из второй и третьей строк вычтем первую, умноженную соответственно на 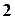и :

;

и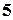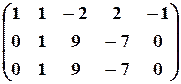з третьей строки вычтем вторую, при этом получим матрицу

,

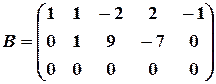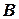которая эквивалентна матрице , так как получена из нее с помощью конечного множества элементарных преобразований. Очевидно, что ранг матрицы равен 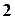, а следовательно, и .

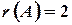Матрицу 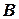легко привести к канонической.

Вычитая первый столбец, умноженный на подходящие числа, из всех последующих, обратим в нуль все элементы первой строки, кроме первого, причем элементы остальных строк не изменяются.

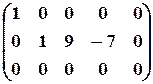
Затем, вычитая второй столбец, умноженный на подходящие числа, из всех последующих, обратим в нуль все элементы второй строки, кроме второго, и получим каноническую матрицу:

.

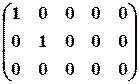
Обратная матрица

Пусть дана квадратная матрица:

.

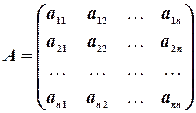Обозначим .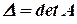

Квадратная матрица называется невырожденной, или неособенной, если ее определитель отличен от нуля, и вырожденной, или особенной, если .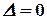

Квадратная матрица 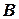называется обратной для квадратной матрицы того же порядка, если их произведени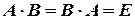е , где 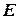- единичная матрица того же порядка, что и матрицы и .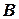

Теорема. Для того чтобы матрица имела обратную, необходимо и достаточно, чтобы ее определитель был отличен от нуля.

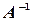Матрица, обратная матрице , обозначается через , так что 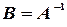. Обратная матрица вычисляется по формуле

,

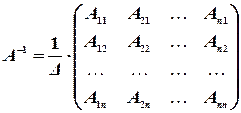где 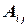- алгебраические дополнения элементов 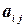. Или

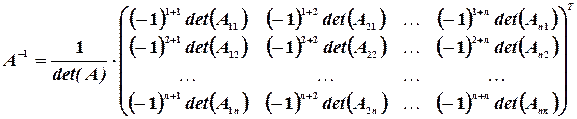
Таким образом, обратная матрица – это транспонированная матрица алгебраических дополнений, умноженная на коэффициент .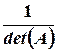

Вычисление обратной матрицы по этой формуле для матриц высокого порядка очень трудоемко, поэтому на практике бывает удобно находить обратную матрицу с помощью метода элементарных преобразований (ЭП).

Любую неособенную матрицу путем ЭП только столбцов (или только строк) можно привести к единичной матрице .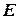

Если совершенные над матрицей ЭП в том же порядке применить к единичной матрице 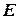, то в результате получится обратная матрица. Удобно совершать ЭП над матрицами и 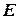одновременно, записывая обе матрицы рядом через черту.

Замечание. Отметим, что при отыскании канонического вида матрицы с целью нахождения ее ранга можно пользоваться преобразованиями строк и столбцов. Если нужно найти обратную матрицу, в процессе преобразований следует использовать только строки или только столбцы.

Пример 15. Для матрицы 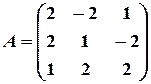найти обратную ей матрицу.

Решение. Находим сначала детерминант матрицы (для этого прибавляем ко второму столбцу первый, а от третьего отнимаем первый, деленный на два):

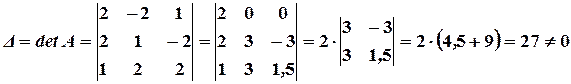
значит, обратная матрица существует, и мы ее можем найти по формуле:

,

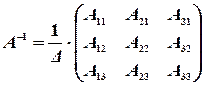где 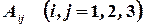‑ алгебраические дополнения элементов 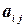исходной матрицы.

, _,

_{, ,}

_{, ,}

_{, ,}

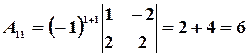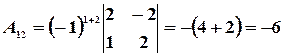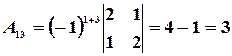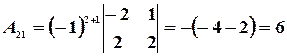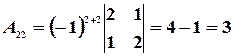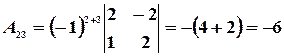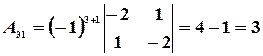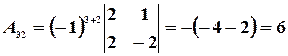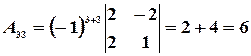
Откуда

.

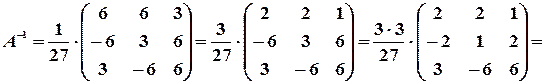
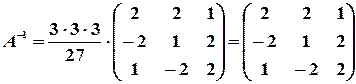Пример 16. Методом элементарных преобразований найти обратную матрицу для матрицы: .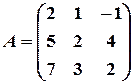

Решение. Приписываем к исходной матрице справа единичную матрицу того же порядка: 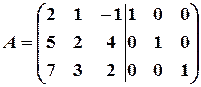. С помощью элементарных преобразований столбцов приведем левую “половину” к единичной, совершая одновременно точно такие преобразования над правой матрицей.

1. Поменяем местами первый и второй столбцы:

.

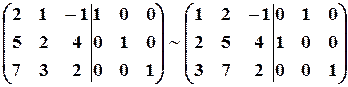2. К третьему столбцу прибавим первый, а ко второму - первый, умноженный на :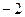

.

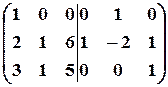3. Из первого столбца вычтем удвоенный второй, а из третьего - умноженный на 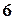второй;

.

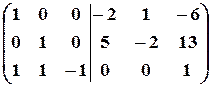4. Прибавим третий столбец к первому и второму:

.

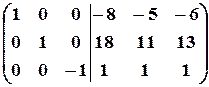5. Умножим последний столбец на :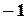

.

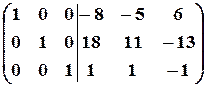Полученная справа от вертикальной черты квадратная матрица является обратной к данной матрице . Итак,

.

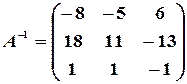Системы линейных уравнений.

Система линейных уравнений имеет вид:

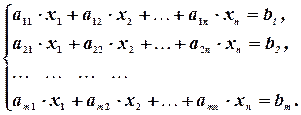
Здесь 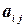и 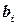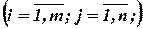‑ заданные, а 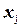‑ неизвестные действительные числа. Используя понятие произведения матриц, можно переписать систему в виде:

AX =B

где 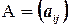- матрица, состоящая из коэффициентов при неизвестных, которая называется матрицей системы, 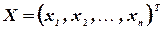, 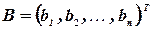- векторы-столбцы, составленные соответственно из неизвестных x_j и из свободных членов b_i.

Упорядоченная совокупность 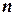вещественных чисел 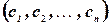называется решением системы, если в результате подстановки этих чисел вместо соответствующих переменных 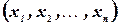каждое уравнение системы обратится в арифметическое тождество.

Система называется совместной, или разрешимой, если она имеет по крайней мере одно решение. Система называется несовместной, или неразрешимой, если она не имеет решений.

Матрица

,

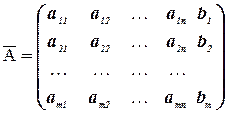образованная путем приписывания справа к матрице A столбца свободных членов, называется расширенной матрицей системы.

Вопрос о совместности системы решается следующей теоремой.

Теорема Кронекера-Капелли.

Система линейных уравнений совместна тогда и только тогда, когда ранги матриц A и 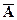совпадают, т.е. .

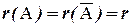Система имеет единственное решение только в том случае, когда
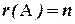. При этом число уравнений - не меньше числа неизвестных 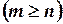; если 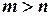, то 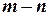уравнений являются следствиями остальных. Если 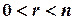, то система является неопределенной.

Для решения произвольной системы линейных уравнений нужно уметь решать системы, в которых число уравнений равно числу неизвестных, - так называемые системы крамеровского типа:

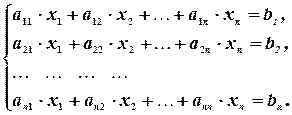
Эти системы решаются одним из следующих способов:

1) методом Гаусса, или методом исключения неизвестных;

2) по формулам Крамера;

3) матричным методом.

Пример 17. Исследовать систему уравнений и решить ее, если она совместна:

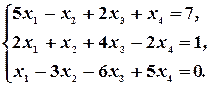
Решение. Выписываем расширенную матрицу системы:

.

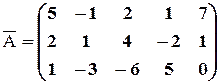Вычислим ранг основной матрицы системы. Очевидно, что, например, минор второго порядка в левом верхнем углу 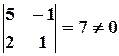; содержащие его миноры третьего порядка равны нулю:

, .

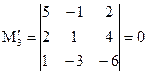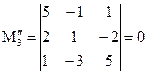Следовательно, ранг основной матрицы системы равен 2, т.е. 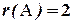. Для вычисления ранга расширенной матрицы 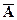рассмотрим окаймляющий минор

,

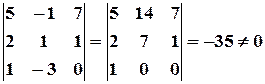значит, ранг расширенной матрицы 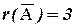. Поскольку 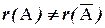, то система несовместна.

А. Метод Гаусса

Исторически первым, наиболее распространенным методом решения систем линейных уравнений является метод Гаусса, или метод последовательного исключения неизвестных. Сущность этого метода состоит в том, что посредством последовательных исключений неизвестных, данная система превращается в ступенчатую (в частности, треугольную) систему, равносильную данной. При практическом решении системы линейных уравнений методом Гаусса удобнее приводить к ступенчатому виду не саму систему уравнений, а расширенную матрицу этой системы, выполняя элементарные преобразования над ее строками. Последовательно получающиеся в ходе преобразования матрицы обычно соединяют знаком эквивалентности.

Пример 18. Решить систему уравнений методом Гаусса:

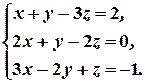
Решение. Выпишем расширенную матрицу данной системы

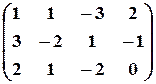
и произведем следующие элементарные преобразования над ее строками:

а) из ее второй и третьей строк вычтем первую, умноженную соответственно на 3 и 2:

;

б) третью строку умножим на (-5) и прибавим к ней вторую:

.

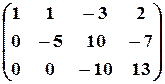В результате всех этих преобразований данная система приводится к треугольному виду:

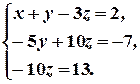
Из последнего уравнения находим 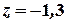. Подставляя это значение во второе уравнение, имеем 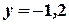. Далее из первого уравнения получим .

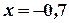Б. Формулы Крамера

Назовем столбцы матрицы следующим образом: первый столбец - 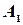, второй столбец - 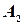, и т.д., последний столбец - 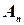. Тогда матрицу 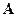можно записать в виде .

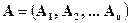Составим 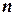дополнительных матриц:

, , …, ,

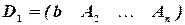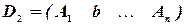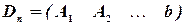и вычислим их определители и определитель исходной матрицы:

, , , …, .

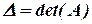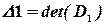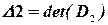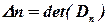Тогда значения неизвестных вычисляются по формулам Крамера:

, , …, .

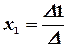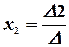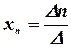Правило Крамера дает исчерпывающий ответ на вопрос о совместности системы: если главный определитель системы отличен от нуля, то система имеет единственное решение, определяемое по вышеприведенным формулам.

Если главный определитель системы 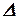и все вспомогательные определители 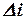равны нулю, то система имеет бесчисленное множество решений.

Если главный определитель системы 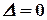, а хотя бы один вспомогательный определитель отличен от нуля, то система несовместна.

Пример 19. Решить систему уравнений методом Крамера.

, .

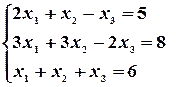
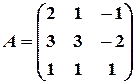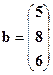Тогда

, , .

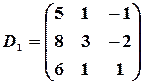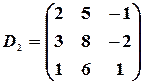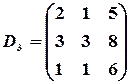Вычисляя определители этих матриц, получаем , , , .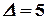

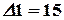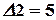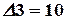И по формулам Крамера находим: , , .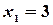

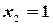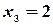В. Матричный метод

Теперь, рассмотрим матричное уравнение 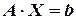. Если у матрицы существует обратная матрица 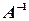, то, умножая матричное уравнение на 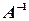слева, получим:

.

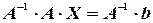По определению обратимости матрицы 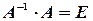и по свойству единичной 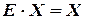, получаем:

.

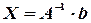Пример 20. Решить систему уравнений с помощью обратной матрицы.

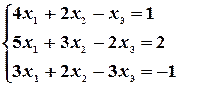
Имеем:

, .

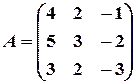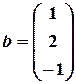Вычислим определитель матрицы , разлагая по первой строке:

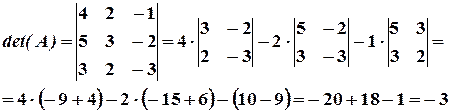
Значит, обратная матрица существует. Вычислим алгебраические дополнения элементов матрицы:

, ,

, ,

, ,

, ,

.

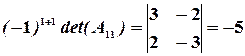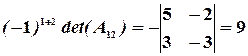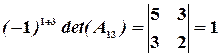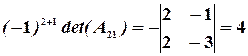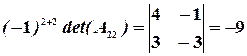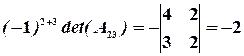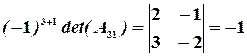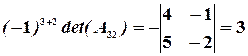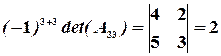Тогда решение системы получается умножением обратной матрицы на столбец свободных членов