Структурный синтез конечных автоматов.

Как отмечалось выше, синтез конечного автомата сводится к его проектированию из более простых элементарных автоматов. Отсюда следует, что для синтеза автомата требуется определить тип элементарного автомата и его функционально полную систему логических элементов (если они не заданны в задании на проектирование).

Число элементарных автоматов К, которое потребуется для синтеза заданного автомата с n внутренними состояниями, определяется как ближайшее целое число по формуле К= log₂n .

В процессе кодирования каждое внутреннее состояние заданного автомата отождествляется с набором внутренних состояний элементарных автоматов s₁,s₂,…,s_k . Так как состояние каждого элементарного автомата кодируется двоичным кодом, то каждому внутреннему состоянию заданного автомата ставится в соответствие к-разрядное двоичное число.

По некоторым соображениям (например, устойчивость работы) число разрядов К внутренних состояний автомата может быть увеличено.

Отметим, что в связи с тем, что заданный автомат реализуется на элементарных автоматах, которые задаются как автоматы Мура, то функция переходов заданного автомата совпадает с его внутренним состоянием. На практике способ кодирования внутренних состояний часто бывает заданным.

Пример. Синтезировать автомат, который при подаче на него входного сигнала x=0, меняет свое состояние в последовательности 0,1,3,2,0,1…, а при подаче сигнала x=1, меняет свое состояние в последовательности 0,2,1,3,0,1….

Число состояний автомата n=4. Определим число элементарных автоматов (триггеров) как К= log₂4 =2.

Выберем для синтеза автомата триггеры типа D, внутренние состояния будем кодировать прямым двоичным кодом, а в качестве логических элементов используем основной базис (И, ИЛИ, НЕ).

Составим таблицу переходов заданного автомата (табл. 3.24).

Табл. 3.24

X(t)	Q1(t)	Q2(t)	Q1(t+1)	Q2(t+1)	D1(t)	D2(t)

Запишем функции выходов для триггеров, на которых реализуется автомат. Эти функции часто называют функциями возбуждения триггеров.

D₁(t+1)=x(t)Q₁(t)Q₂(t)+x(t)Q₁(t)Q₂(t)+x(t)Q₁(t)Q₂(t).

D₂(t+1)=x(t)Q’₁(t)Q₂(t)+x’(t)Q₁(t)Q₂(t)+x(t)Q₁(t)Q₂(t)+x(t)Q₁(t)Q₂(t)

Минимизируем полученные функции методом карт Вейча (табл 3.25)

Табл 3.25

Q₁(t) D1 Q₁(t) D2

x(t)						x(t)

Q₂(t) Q₂(t)

a б

Функция возбуждения для первого триггера запишется в виде D₁(t)=x(t)Q’₁(t)+x’(t)Q₂(t), а для второго триггера D₂(t)=x(t)Q₁(t)Q’₂(t)+Q’₁(t)Q₂(t)+x’(t)Q’₁(t).

На рис. 3.6. Приведена схема, реализующая заданный автомат.

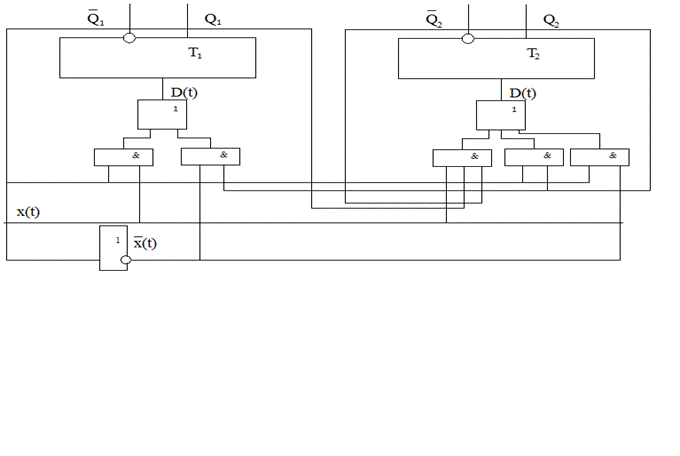
Рис.3.6. Схема, реализующая автомат на D триггере.

Пример. Синтезировать автомат из предыдущего примера, но использовать триггеры типа j-k и элементы И-НЕ.

Число триггеров для синтеза автомата, как и в предыдущем примере равно двум.

Составим таблицу переходов заданного автомата (табл.3.25)

X(t)	Q1(t)	Q2(t)	Q1(t+1)	Q2(t+1)	J1(t)	K1(t)	J2(t)	K2(t)
						b1		b2
						b2	b4
					b3			b1
					b4		b3
						b2		b1
						b2	b4
					b3		b3
					b3			b2

Составим функцию возбуждения по каждому из входов триггеров.

J₁(t)=x’(t)Q’₁(t)Q₂(t)+x(t)Q’₁(t)Q’₂(t)+x(t)Q’₁(t)Q₂(t);

Наборы значения элементов на которых функция не определена

<x(t)Q₁(t)Q₂(t)= b₃; x(t)Q₁(t)Q₂(t)= b₄; x(t)Q₁(t)Q₂(t)= b₃; x(t)Q₁(t)Q₂(t)= b₃>

K₁(t)=x(t)Q₁(t)Q₂(t)+x(t)Q₁(t)Q₂(t)+ x(t)Q₁(t)Q₂(t); наборы значений аргументов, на которых функция не определена

<x(t)Q₁(t)Q₂(t)= b₁; x(t)Q₁(t)Q₂(t)= b₂; x(t)Q₁(t)Q₂(t)= b₂; x(t)Q₁(t)Q₂(t)= b₂>

J₂(t)=x(t)Q₁(t)Q₂(t)+x(t)Q₁(t)Q₂(t); наборы значений элементов, на которых функция не определена

Таблица 3. 25. <x(t)Q₁(t)Q₂(t)= b₄; x(t)Q₁(t)Q₂(t); x(t)Q₁(t)Q₂(t)= b₄; x(t)Q₁(t)Q₂(t)= b₃>

K₂(t)=x(t)Q₁(t)Q₂(t)+ x(t)Q₁(t)Q₂(t); функция не определена на наборе значений аргументов

<x(t)Q₁(t)Q₂(t)= b₂; x(t)Q₁(t)Q₂(t)= b₁; x(t)Q₁(t)Q₂(t)= b₁; x(t)Q₁(t)Q₂(t)= b₂>

Составим карты Вейча для каждой функции возбеждения триггеров (табл.3.26)

Q₁(t) Q₁(t) Q₁(t)

x(t)

b3

b3

x(t)

b2

b2

x(t)

b3

b4

b3

b4

b2

b1

b4

Q₂(t) Q₂(t) Q₂(t)

a (J₁(t)) б (K₁(t)) в (J₂(t))

Q₁(t)

x(t)	b2			b1
	b2			b2

Q₂(t)

г (K₂(t))

Выразим функцию возбеждения триггеров в базисе функции Шеффера (И-НЕ)

J₁(t)=x(t)+Q₂(t)=[x(t)∙x(t)+Q₂(t)∙Q₂(t)]={[x(t)|x(t)]|[Q₂(t)|Q₂(t)]

K₁(t)=x(t)+Q₂(t)=[x(t)∙x(t)+Q₂(t)∙Q₂(t)]={[x(t)|x(t)]|[Q₂(t)|Q₂(t)]}

J₂(t)=x(t)Q₁(t)+x(t)Q₁(t)=[x(t)Q₁(t)]+[x(t)Q₁(t)]={[x(t)|Q₁(t)]|[x(t)|Q₁(t)]}

K₂(t)=Q₁(t)Q₂(t)=[Q₁(t)|Q₂(t)]|[Q₁(t)|Q₂(t)]

На рисунке 3.7. приведена схема заданного автомата, реализованного на триггерах типа j-k и элементах И-НЕ.

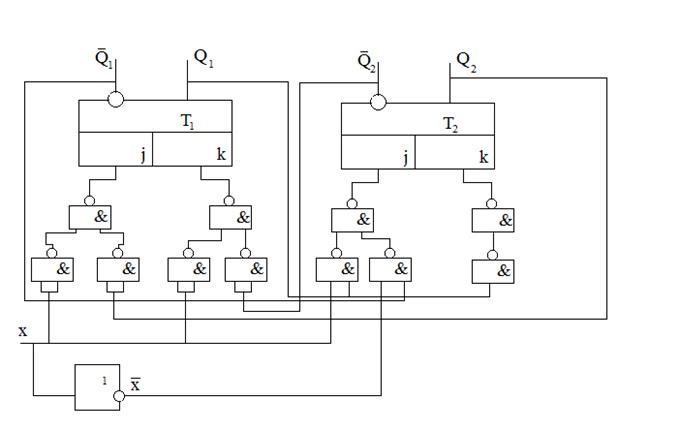
Рис.3.7. Автомат на триггерах j-k и элементах И-НЕ.

Пример. Синтезировать реверсивный регистр, осуществляющий сдвиг хранящейся в нем информации на один разряд влево и вправо. Синтез осуществить на триггерах типа D.

Так как необходимо выполнить две микрооперации – сдвиг информации влево и вправо, то потребуется одна шина управления х. пусть при х=0 происходит сдвиг информации вправо, а при х=1 – влево.

Поскольку структура регистра регулярна, т.е. все разряды регистра идентичны, то функции возбуждения определим только для одного i-го разряда, а функции возбуждения для других триггеров регистра будут аналогичны для всех i=(1,n), где n – число разрядов регистра.

Составим таблицу переходов для i-го разряда регистра (табл.3.27). Отметим, что при х=0, выход триггера Q_i(t+1)=Q_i+1(t), а при х=1, Q_i(t+1)=Q_i-1(t).

Табл. 3.27

x(t)	Qi+1(t)	Qi(t)	Qi-1(t)	Qi(t+1)	Di(t)

По таблице переходов запишем функцию возбуждения входов для i-го разряда регистра D_i(t).

D_i(t)=x(t)Q_i+1(t)Q_i(t)Q_i-1(t)+x(t)Q_i+1(t)Q_i(t)Q_i-1(t)+ x(t)Q_i+1(t)Q_i(t)Q_i-1(t)+ +x(t)Q_i+1(t)Q_i(t)Q_i-1(t)+ x(t)Q_i+1(t)Q_i(t)Q_i-1(t)+ x(t)Q_i+1(t)Q_i(t)Q_i-1(t)+ x(t)Q_i+1(t)Q_i(t)Q_i-1(t)+

+ x(t)Q_i+1(t)Q_i(t)Q_i-1(t)

Минимизируем полученную функцию возбуждения входов методом карт Вейча (Рис3.7)

		Qi+1(t)					В результате минимизации функция запишется в виде Di(t)=x(t)Qi-1(t)+x(t)Qi+1(t)
x(t)
						Qi(t)
			Qi-1(t)

Рис.3.7. Карта Вейча для минимизации функции D_i(t)

Отметим, что в схеме должны присутствовать входы синхронизации (с), установки триггеров в состоянии единица (S), установки триггеров в ноль (R) и информационные входы (D).

При записе в регистр все триггеры устанавливаются в ноль, путем подачи соответствующего сигнала на входы R, а затем на входы S подается информационное слово.