Минимизация булевых функций с помощью карт Вейча.

Это наиболее удобный метод минимизации булевых функций при небольшом числе переменных.

Карта Вейча для двух переменных (а), для трех (б), для четырех (в), для пяти (г), представляет собой таблицу с определенным порядком следования наборов (в клетках таблицы – номера минтермов соответствующего числа переменных) (рис.1.3).

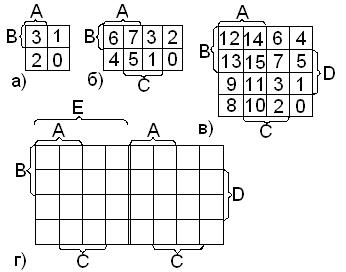
Рис.1.3.

Для удобства пользования картами на полях проставляют значения переменных.

Таблица функции записывается в карту обычным способом 1(0) – в квадратах, соответствующих наборам, где f(x₁ x₂ … x_n)=1(0).

Следует иметь виду, что порядок расположения наборов таков, что при переходе между соседними квадратами по строке или столбцу меняется форма лишь одной переменной в наборе. В этом смысле первая строка карты является соседней с последней, а первый столбец – соседний с последним.

Отсюда возникают возможности проведения операции склеивания, исходя из расположения единиц в карте Вейча.

Правила склеивания с помощью карт Вейча.

Два минтерма склеиваются (рис.1.4), если они расположены:

1) по соседству – в одной строке или одном столбце (рис.1.4,а);

2) в противоположных концах одной строки или одного столбца (рис.1.4,б);

3) в одинаковых местах двух карт (рис.1.4,в), последнее – для n>4.

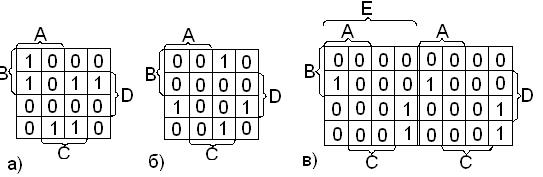
рис.1.4.

Алгоритм метода минимизации с помощью карт Вейча.

1) Нанести функцию на карту.

2) Каждый квадрат, содержащий «1», проанализировать с точки зрения «склеивания» с другими во всех возможных комбинациях.

3) Выбираются те комбинации, которые объединяют наибольшее количество единиц и при этом накрывают все единицы карты функции. Они являются простыми импликантами функции.

4) Если только одна импликанта покрывает какую-либо единицу на карте, то эта импликанта является существенной (обязательной).

5) Из совокупности простых импликант выбираются минимальные формы функции.

Метод позволяет получить все возможные МДНФ:

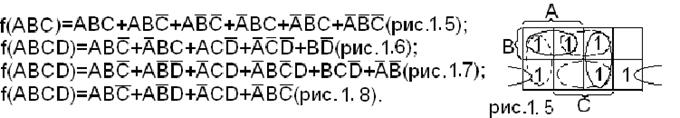
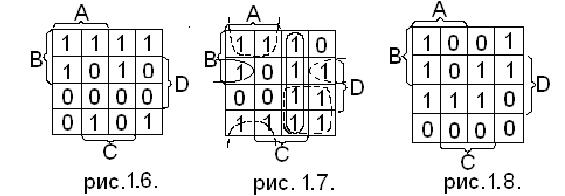
Метод Блека-Порецкого.

Используется для получения сокращенной ДНФ из любой произвольной функции представления [5].

Идея построения сокращенной ДНФ по произвольной ДНФ вытекает из следующего определения: если в ДНФ для данной функции f(x₁ … x_n) входит две конъюнкции вида Ax_i и Bx_i, то имеет место равенство D=D\/AB, где D – ДНФ, эквивалентная функция f.

Алгоритм метода Блека-Порецкого.

1. Провести все возможные склеивания любых двух смежных термов, представляющих соответствующие элементарные конъюнкции, получить L-разрядный троичный набор и построить матрицу ранга n.

2. Над полученными элементарными конъюнкциями ранга (n-1) провести операции склеивания и поглощения, образовать элементарные конъюнкции нижнего ранга и т.д.

3. Процесс закончить, когда после операции склеивания и поглощения окажется, что в ДНФ отсутствуют члены, дальнейшее поглощение которых невозможно, т.е. когда будет получена сокращенная ДНФ.

4. Строится импликантная матрица и определяется максимальное покрытие.

Метод удобен при машинных способах минимизации.

Пример. Найти минимальную форму для заданной функции:

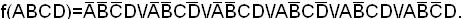
1. Матрица исходных данных 3. Матрица ранга (n-2)

0 0 0 1 2 0 2 1

0 0 1 0 2 0 2 1

0 0 1 1 2 0 1 2

1 0 0 1 2 0 1 2

1 0 1 0

1 0 1 1

2. Матрица ранга (n-1)*

0 0 2 1

2 0 0 1

0 0 1 2

2 0 1 0

2 0 1 1

1 0 2 1

1 0 1 2

4. Вычеркиваем одинаковые строки матрицы ранга (n-2) и получаем

A B C D

2 0 2 1

2 0 1 2

5.

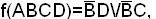
где 0 – инверсия переменной, 1 – переменная, 2 – отсутствует переменная.