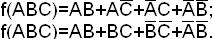Сокращенные, тупиковые и минимальные формы булевых функций.

ДНФ (КНФ) называется минимальной, если количество букв, которые она содержит, будет не больше, чем в любой другой ДНФ (КНФ) той же функции.

Пусть на каком-то наборе аргументов функция f₁(x₁ x₂ … x_n) принимает значение α₁ , а функция f₂(x₁ x₂ … x_n) - значения α₂ . Тогда говорят, что функция f₁ на данном наборе накрывает значение α₂ функции f₂ своим значением α₁.

Аналогично можно сказать, что функция f₂ на данном наборе накрывает значение α₁ функции f₁ своим значением α₂.

Пример. f₁₁(xy)= m₀+m₁+m₃.

Каждый минтерм накрывает своим значением единица на соответствующем наборе единичное значение функции f₁₁ , а все минтермы, входящие в СДНФ функции, накрывают значениями единица все единицы функции.

Определение. Если некоторая булева функция [V1] φ равна нулю на тех же наборах, на которых равна нулю другая функция f, то говорят, что функция φ входит в функцию f:

.

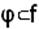Таким образом, функция φ накрывает нулями все нули функции f и, следовательно, имеет не меньше нулей, чем функция f.

Пример.

а) Любой минтерм СДНФ функции f входит в f; f₆(xy)= m₁+m₂ и равна 0 на наборах <00>, <11>

f₀(xy) f₆(xy);

f₄(xy) f₆(xy);

f₂(xy) f₆(xy);

б) Функция f₀=0 – входит в любую булеву функцию.

в) В функцию

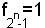
- входят все функции n переменных.

Определение. Функция φ, входящая в данную функцию f, называется ее импликантой.

Собственной частью конъюнкции называется конъюнкция, полученная из данной конъюнкции путем исключения одного или нескольких сомножителей.

Простыми импликантами булевой функции называются такие элементарные конъюнкции, которые сами входят в данную функцию, но никакая собственная часть этих конъюнкций в эту функцию не входит.

Пример. 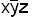имеет собственные части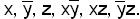

Пример. Пусть выполняется условие

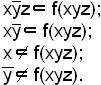
Значит, 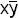- простая импликанта функции f(xyz).

Пример. Рассмотрим функцию, представленную в табл.1.16.

Таблица 1.16

x 0 0 0 0 1 1 1 1

y 0 0 1 1 0 0 1 1

z 0 1 0 1 0 1 0 1

f(xzy) 0 0 0 0 1 0 1 1

xyz 0 0 0 0 0 0 0 1

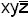0 0 0 0 0 0 1 0

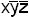0 0 0 0 1 0 0 0

xy 0 0 0 0 0 0 1 1

В эту функцию входят xyz, 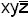, , 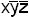xy, так как они равны нулю на всех наборах, где f(xyz)=0, но простыми импликантами будут 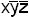и xy.

Теорема. Любая булева функция равна дизъюнкции всех своих простых импликант.

Доказательство. Так как все простые импликанты входят в данную функцию (по определению), то они равны нулю на всех наборах, на которых функция равна нулю. Следовательно, и дизъюнкция их равна нулю на тех наборах, где равна нулю функция.

Так как СДНФ функции есть дизъюнкция элементарных конъюнкций, а простые импликанты есть собственные части этих конъюнкций, то на тех наборах, где СДНФ функции равна 1, обязательно равна единице и одна из простых импликант. Таким образом, дизъюнкция простых импликант принимает значения 1 на тех же наборах, что и сама функция.

Теорема доказана.

Дизъюнкция всех простых импликант называется сокращенной ДНФ функции. Любая переключательная функция имеет единственную сокращенную ДНФ.

Метод Квайна.

Этот метод используется для получения сокращенной ДНФ функции из СДНФ ее с помощью операций неполного склеивания:

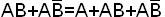
и поглощения A+AB=A.

Теорема Квайна. Если в СДНФ булевой функции провести все операции неполного склеивания, а затем все операции поглощения, то получится сокращенная ДНФ этой функции, т.е. дизъюнкция всех ее простых импликант.

Доказательство теоремы проверять не будем.

Чтобы получить все простые импликанты, так как один и тот же член дизъюнктивной формы может склеиваться с несколькими другими, образуя при этом различные импликанты, после склеивания исходный член следует сохранить.

Алгоритм метода Квайна.

1) Провести все возможные склеивания минтермов, входящих в СДНФ функции. В результате образуются элементарные конъюнкции ранга (n-1).

2) Так как склеиваться могут только элементарные конъюнкции одного ранга, то в дальнейших склеиваниях минтермы не участвуют, поэтому следует выполнить операции поглощения.

3) Над полученными элементарными конъюнкциями ранга (n-1) повторить операции склеивания и поглощения, образовав элементарные конъюнкции нижнего ранга, и т.д.

4) Процесс заканчивается, когда дальнейшее склеивание оказывается невозможным.

5) Оставшиеся в результате поглощения элементарные конъюнкции являются простыми импликантами функции, а дизъюнкция их есть сокращенная ДНФ функции.

Пример. Найти сокращенную ДНФ функции:

СДНФ функции

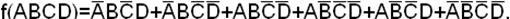
Приводим алгоритм метода:

Здесь \/ - отметка поглощения.

Сокращенная ДНФ функции:

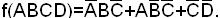
Пример. Найти сокращенную ДНФ функции:

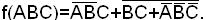
СДНФ функции

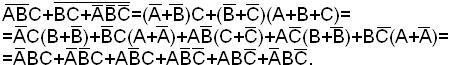
Проводим операции склеивания и поглощения:

Сокращенная ДНФ функции

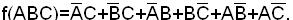
Гарвардский метод.

Метод, разработанный в Гарвардском университете, позволяет находить сокращенную ДНФ функции с использованием специальных карт для записи булевых функций соответствующего числа переменных.

В столбцах карт перечислены все элементарные конъюнкции функции n переменных, содержащие от 1-й до n букв.

Алгоритм Гарвардского метода.

1) Внести в карту для функции соответствующего числа переменных значения функции на всех наборах.

2) Вычеркнуть все строки, где записаны нулевые значения функции.

3) В каждом столбце таблицы вычеркнуть числа, совпадающие с числами в вычеркнутых строках данного столбца.

4) Из каждой не вычеркнутой строки выбрать элементарную конъюнкцию, содержащую наименьшее количество букв двоичный эквивалент которой остался не зачеркнутым.

Пример. Найти сокращенную ДНФ функции:

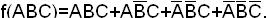
Карта для заданной функции приведена в табл.1.17.

В результате получаем

.

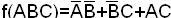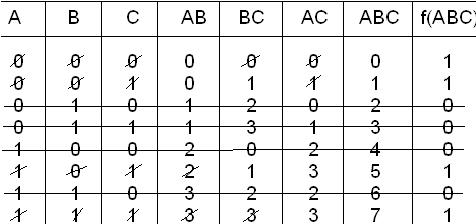
Нетрудно убедиться, что в полученной сокращенной ДНФ импликанту 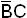можно исключить:

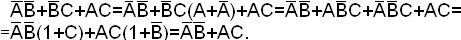
Таблица 1.17.

Простая импликанта, которую нельзя исключить из сокращенной ДНФ функции, называется существенной импликантой.

Дизъюнкция существенных импликант функции называется тупиковой ДНФ заданной функции.

Некоторые булевы функции имеют несколько тупиковых форм. Тупиковая ДНФ функции называется минимальной (МДНФ), если количество букв, которое она содержит, будет не больше, чем в любой другой ДНФ той же функции.

Отсюда следует, что для отыскания минимальных форм достаточно получить все тупиковые формы заданной функции и выбрать среди них минимальные.

Метод импликантных матриц.

Рассмотрим графический метод отыскания тупиковых форм функции из сокращенной ДНФ.

Импликантная матрица представляет собой таблицу, столбцы которой соответствуют всем конституентам единицы СДНФ заданной функции, а строки – всем простым импликантам.

В таблице по строке каждой импликанты отмечаются те минтермы, которые ею поглощаются.

Чтобы получить минимальную ДНФ заданной функции, достаточно найти минимальное число импликант, которые совместно накрывают все столбы импликантной матрицы, если в каком-либо из столбцов составленной импликантной матрицы функции имеется только одна отметка, то соответствующая ей импликанта является обязательной и обязательно входит в тупиковую форму функции, так как без нее будет получено накрытие всего множества минтермов.

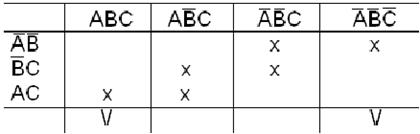
Для случая имеем импликантную матрицу, представленную в табл.1.18.

В данном случае импликанты AC и 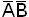являются обязательными. Их сумма покрывает все минтермы, следовательно, тупиковая форма 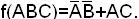Она единственна и поэтому является минимальной.

Таблица 1.18.

Пример. Найти минимальную ДНФ функции, используя метод Квайна и метод импликантных матриц:

Сокращенная ДНФ

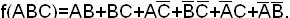
Импликантная матрица функции дана в табл.1.19.

Таблица 1.19

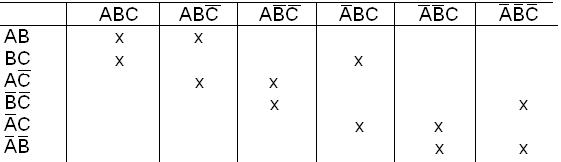
Так как нет столбцов с одной отметкой, то ни одна из импликант не является обязательной. Найдем минимальное количество простых импликант, накрывающее все колонки.

Возможны две тупиковые формы функции:

;

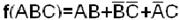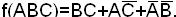
Обе формы содержат одинаковое число букв и, следовательно, обе являются минимальными.

Возможны другие тупиковые формы данной функции, но они не минимальны: