Способы выявления равносильности булевых функций.
Как табличная запись функции, так и запись функции в СДНФ и в СКНФ являются единственными, поэтому для доказательства равносильности булевых функций используются следующие способы:
1) Сравнение табличных записей функций по всем возможным наборам переменных.
Пример. Доказать тождество f248(ABC)= 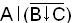 (табл. 1.9,1.10).
(табл. 1.9,1.10).
Таблица 1.9 Таблица 1.10
 |  |
A B C f248(ABC) A B C B↓C 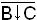
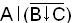

 0 0 0 1 0 0 0 1 0 1
0 0 0 1 0 0 0 1 0 1
0 0 1 1 0 0 1 0 1 1
0 1 0 1 0 1 0 0 1 1
0 1 1 1 0 1 1 0 1 1
1 0 0 1 1 0 0 1 0 1
1 0 1 0 1 0 1 0 1 0
1 1 0 0 1 1 0 0 1 0
1 1 1 0 1 1 1 0 1 0
248=128+64+32+16+8=27+26+25+24+23=111110002.
Так как значение функций на всех наборах совпадает, то f248(ABC)= 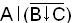 и тождество доказано.
и тождество доказано.
Способ доказательства равносильности функций по таблицам очень нагляден, но при большом числе n затруднителен.
2) Сравнение СДНФ и СКНФ функций.
Пример. Доказать тождество f196(ABC)=  ;
;
19610=128+64+4=27+26+22=110001002.
В индексе функции единиц меньше, чем нулей, следовательно, СДНФ функции имеет более короткую запись, чем СКНФ:
f196(ABC)= m0+m1+m5;

= m0+m1+m5.
СДНФ функций совпадают, следовательно, тождество доказано.
Пример. Доказать тождество
F237(ABC)=  ;
;
237(10)=128+64+32+8+4+1=27+26+25+23+22+20=11101101(2),
так как нулей мало, используем СКНФ:
f237(ABC)= М4 М1 ;

СКНФ функций совпадают, тождество доказано.
3) Преобразование одной из сравниваемых функций с помощью основных соотношений до полного совпадения с другой. Этот способ не поддается алгоритмизации, и поэтому, если не удалось привести функции к одному виду, то еще нельзя утверждать, что эти функции неравносильны.
Пример. Доказать тождество  ;
;


Тождество доказано.
Свойства функций сложения по модулю 2.
Основные соотношения для функции:  :
:
ассоциативный закон

коммутативный закон

дистрибутивный закон относительно функции конъюнкции

а также 

 x при n нечетном;
x при n нечетном;
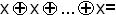
 0 при n четном.
0 при n четном.
n
В справедливости этих соотношений можно убедиться, если вместо  подставить СДНФ этой функции:
подставить СДНФ этой функции:

Пример. Доказать равносильность функций 
а) аналитически

б) с помощью таблиц истинности (табл.1.11,1.12) функций:
Таблица 1.11 Таблица 1.12
 |  |
x y xy 
 x y x+y
x y x+y


0 0 0 0 0 0 0 0
0 1 0 1 1 0 1 1
1 0 0 0 1 1 0 1
1 1 1 0 1 1 1 1
Пример. Доказать равносильность функций  с помощью таблиц истинности (табл.1.13, 1.14).
с помощью таблиц истинности (табл.1.13, 1.14).
Таблица 1.13 Таблица 1.14
 |  |
x y 

 x y xy
x y xy


0 0 1 0 0 0 0 0
0 1 0 0 0 0 1 0
1 0 1 1 0 1 0 0
1 1 0 0 1 1 1 1
Теорема Жегалкина: любая булева функция может быть представлена в виде многочлена
f(x1 x2 … xn)= α0 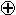 α1 x1
α1 x1 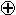 α2 x2
α2 x2 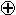 …
… 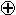 αn xn
αn xn 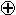 αn+1
αn+1 
 x1 x2
x1 x2 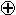 αn+2 x1 x3
αn+2 x1 x3 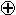 …
… 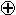 αN x1 x2 … xn ,
αN x1 x2 … xn ,
где α0, α1, … , αN - некоторые константы, равные 0 или 1.
Для доказательства воспользуемся основной теоремой, утверждающей, что любую булеву функцию можно записать в виде 2n-1
f(x1 x2 … xn)= 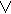 α i mi .
α i mi .
i=0
Для любого конкретного набора < x1 x2 … xn > из тех наборов, на которых функция принимает значение 1, только один минтерм обращается в единицу, а остальные равны нулю. Поэтому справедлива запись 2n-1
f(x1 x2 … xn)=  α i mi .
α i mi .
i=0
От этой формы записи можно перейти к функции в виде полинома через операции 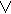 и
и 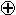 , пользуясь соотношением
, пользуясь соотношением  .
.
Пример.  .
.
Таким образом, после приведения подобных членов функция f(x1 x2 … xn) будет записана в виде многочлена, при построении которого используются только операции конъюнкции и сложения по mod 2.
Теорема доказана.
Алгоритм построения.
Чтобы булеву функцию, заданную таблицей значений или любым другим способом, представить в виде многочлена, достаточно:
1) записать функцию в виде суммы по mod 2 минтермов, равных единице на тех же наборах, на которых равна заданная функция;
2) все аргументы, входящие в полученное выражение в инверсной форме, заменить с помощью соотношения 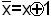 ;
;
3) раскрыть скобки и сделать приведение подобных членов с учетом тождества:
 x, если n нечетно;
x, если n нечетно;
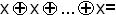
 0, если n четно.
0, если n четно.
n
Пример. Представить в виде многочлена функцию f14(AB):
f7(AB)= m0+m1+m2= m0 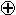 m1
m1 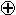 m2=
m2= 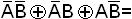
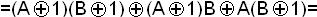
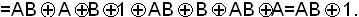
Пример. Представить в виде многочлена функцию f9(AB):
f9(AB)= m0+m3= m0 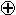 m3=
m3= 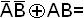
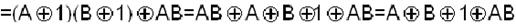 .
.
На базе функции 1, /\ и 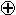 строится алгебра Жегалкина, но по своим свойствам она более близка к обычной алгебре и отличается от последней лишь тем, что логическое сложение заменено сложением по mod 2.
строится алгебра Жегалкина, но по своим свойствам она более близка к обычной алгебре и отличается от последней лишь тем, что логическое сложение заменено сложением по mod 2.
