Функции алгебры логики и их основные свойства.

Рассмотрим набор < x₁, x₂,…, x_n>, где x_i принимает значения 0 или 1: <011010…1>. Число различных наборов такого вида при 1≤i≤n конечно и равно 2ⁿ.

Два различных набора < x₁, x₂,…, x_n> и < y₁, y₂,…, y_n>, где x_i и y_i принимают значения 0 или 1, называются сравнимыми, если для любого i выполняется соотношение x_i ≥ y_i (или x_i ≤ y_i ), и несравнимыми во всех остальных случаях.

Функция f(x₁, x₂,…, x_n) называется булевой или переключательной функцией, если она, так же как и ее аргументы, может принимать только два значения: 0 и 1.

Если две булевых функции f₁(x₁ x₂… x_n) и f₂(x₁ x₂… x_n) принимают на всех возможных наборах значений аргументов одинаковые значения, то функции f₁ и f₂ называются равными:

f₁(x₁ x₂ … x_n) = f₂(x₁ x₂ … x_n).

Функция f(x₁ x₂… x_i-1 x_i x_i+1… x_n) существенно зависит от аргумента x_i, если имеет место соотношение:

f(x₁ x₂… x_i-1 1 x_i+1… x_n) ≠f(x₁ x₂… x_i-1 0 x_i+1… x_n).

В противном случае говорят, что от x_i функция зависит несущественно и x_i является ее фиктивным аргументом.

Теорема. Число различных функций алгебры логики, зависящих от n аргументов, конечно и равно 2ⁿ.

Для доказательства составляем таблицу значений произвольной функции n параметров (табл.1.1).

Таблица 1.1

x₁ x₂ … x_n f₁(x₁ x₂ … x_n)

0 0 . . . 0 α₁

0 0 . . . 1 α₂

. . . . . . . . . . .

1 1 . . . 0 α₂ⁿ_-1

1 1 . . . 1 α₂ⁿ

Задавая тот или иной двоичный набор < α₁ α₂ … α₂ⁿ >, будем описывать одну из возможных функций. Но число таких наборов 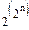= 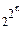. Теорема доказана.

В число функций 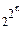входят как функции, существенно зависящие от всех n аргументов, так и функции, для которых некоторые аргументы являются фиктивными.

Теорема. Число всех функций алгебры логики, существенно зависящих от n аргументов, определяется следующим рекуррентным соотношением:

A_n= 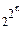- C_n^n-1 A_n-1- C_n^n-1 A_n-1- C_n^n-2 A_n-2-…- C_n¹ A₁- A₀.

Здесь A_i – число функций, существенно зависящих от i аргументов. Правая часть соотношения есть разность между числом всех функций от n аргументов и суммой всех функций, существенно зависящих от любого числа аргументов меньше n. Справедливость очевидна.

Пример. При n=0:

f₀=0, f₁=1, A₀=2.

При n=1 (табл.1.2) f₁ и f₂ зависят от x существенно, а для f₀ и f₃ аргумент x является фиктивным.

Таблица 1.2

x f₀(x) f₁(x) f₂(x) f₃(x)

0 0 0 1 1

1 0 1 0 1

При n=2:

A₂= 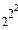- C₂¹ A₁- A₀=10.

При n=3:

A₃= 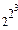- C₃² A₂- C₃¹ A₁- A₀=218.

Область определения любой булевой функции конечна, поэтому все булевы функции можно задать таблицей значений на различных наборах. Так как набор – двоичное число, то принято каждому набору аргументов приписывать номер, равный соответствующему двоичному числу. Причем порядок записи аргументов совпадает с порядком переменных в записи функции:

x₁ x₂ … x_n-1 x_n

0 0 … 0 0 0-й набор

0 0 … 0 1 1-й набор

… … … … … ……..

1 1 … 1 1 (2ⁿ-1)–й набор.

Обычно при задании таблицы наборы идут в порядке возрастания номеров.

Пример. n=0: две функции, существенно не зависящие ни от одного переменного, - константа 0 и 1.

Для n=1 функции сведены в табл.1.3.

Таблица 1.3

x 0 1 Название функции

f₀(x) 0 0 Константа 0

f₁(x) 0 1 Переменная x

f₂(x) 1 0 Инверсия x, не x

f₃(x) 1 1 Константа 1.

В дальнейшем каждой функции будем приписывать номер, равный двоичному числу, образованному значениями функции, записанными слева направо, начиная со значения функции на нулевом наборе.

Для n=2 переключательные функции приведены в табл.1.4.

Таблица 1.4

x 0 0 1 1 Обозначение Название

y 0 1 0 1 функции функции

f₀(xy) 0 0 0 0 0 Константа нуль

f₁(xy) 0 0 0 1 xy, xΛy Логическое произведе-

ние, конъюнкция, Λ

f₂(xy) 0 0 1 0 xΔy Функция запрета по y

f₃(xy) 0 0 1 1 x Переменная x

f₄(xy) 0 1 0 0 yΔx Функция запрета по x

f₅(xy) 0 1 0 1 y Переменная y

f₆(xy) 0 1 1 0 x 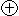y, y 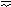x Функция суммы по мо-

дулю 2, логическая не-

равнозначность

f₇(xy) 0 1 1 1 x+y, x 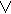y Логическая сумма,

дизъюнкция,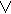

f₈(xy) 1 0 0 0 x↓y Операция (стрелка)

Пирса, операция Вебба

f₉(xy) 1 0 0 1 x~y Логическая

равнозначность

f₁₀(xy) 1 0 1 0 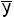Инверсия y, не y

f₁₁(xy) 1 0 1 1 y→x Импликация от y к x

f₁₂(xy) 1 1 0 0 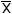Инверсия x, не x

f₁₃(xy) 1 1 0 1 x→y Импликация от x к y

f₁₄(xy) 1 1 1 0 x | y Операция (штрих)

Шеффера

f₁₅(xy) 1 1 1 1 1 Константа единица

При n=2, A₂=10, функции f₀, f₃, f₅, f₁₀, f₁₂ и f₁₅ имеют фиктивные аргументы.

Основные соотношения алгебры логики для функций Λ, 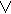и инверсии.

1) Основные законы алгебры логики:

а) ассоциативный (сочетательный) закон

(xy)z=x(yz)=xyz;

(x+y)+z=x+(y+z)=x+y+z;

б) коммутативный (переместительный) закон:

xy=yx;

x+y=y+x;

в) дистрибутивный (распределительный) закон:

(x+y)z=xz+yz;

(x+y)(y+z)=xz+y.

2) Основные соотношения для инверсии:

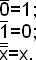
3) Основные соотношения для дизъюнкции:

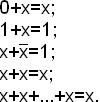
4) Основные соотношения для конъюнкции:

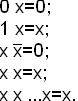
5) Основные соотношения для системы функций:

а) операция поглощения:

x+xy=x;

x(x+y)=x;

б) операция склеивания:

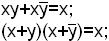
в) формулы де Моргана:

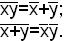
Диаграммы Венна.

Наглядная интерпретация основных соотношений булевых переменных представлена на диаграммах Венна.

Класс булевых переменных определяется как класс, включающий все области внутри квадрата (рис.1.1).

рис.1.1

Любой элемент А этого класса представлен областью, ограниченной замкнутой кривой. 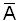- совокупность точек квадрата, не входящих в область А.

Здесь 0 представлен как класс, совсем не имеющий точек, а 1 – как класс всех точек квадрата.

А+В – наименьшая область, содержащая одновременно А и В.

АВ – наибольшая область, содержащаяся одновременно и в А, и в В. Диаграм-мы Венна для элементарных булевых функций изображены на рис.1.2:

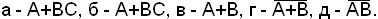
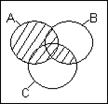
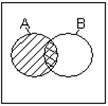
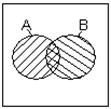
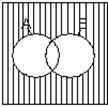
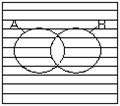
а) б) в) г) д) рис.1.2