Разложение булевой функции по переменным
Обозначим через 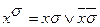 . Тогда
. Тогда
xs= 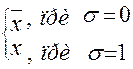
В частности, 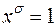 тогда и только тогда, когда
тогда и только тогда, когда 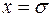 .
.
С помощью “степенной функции” 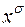 всякую булеву функцию
всякую булеву функцию 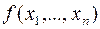 можно представить в виде:
можно представить в виде:
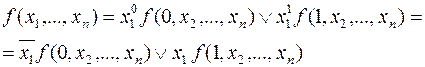
называемом разложением булевой функции 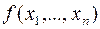 по переменной
по переменной 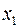 .
.
В самом деле, если 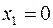 , то
, то 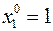 ,
, 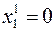 и
и
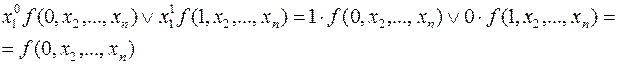
Если 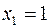 , то
, то 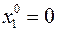 ,
, 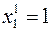 и
и
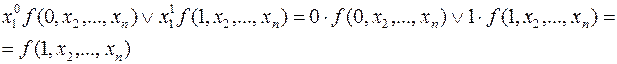
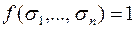
Пример 4.
Разложим функцию 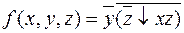 по переменной
по переменной 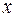 . Для этого сначала построим таблицу функции
. Для этого сначала построим таблицу функции 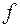 :
:
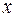 | 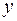 | 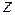 | 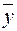 | 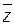 | 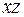 | 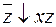 | 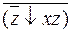 | 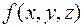 |
Из таблицы видно, что 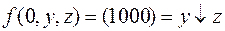 и
и 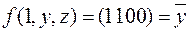 .
.
Используя формулу разложения по переменной 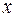 , находим
, находим
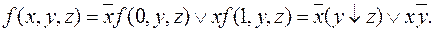
Итак, 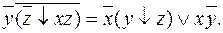
Пример 5.
Разложим функцию 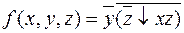 из примера 4 по всем переменным. Так как функция принимает значение 1 на трех наборах:
из примера 4 по всем переменным. Так как функция принимает значение 1 на трех наборах: 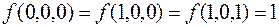 , то согласно следствию из теоремы о разложении, имеем
, то согласно следствию из теоремы о разложении, имеем
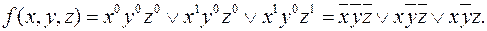
Итак, 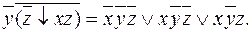
Определение 3.
Разложение булевой функции 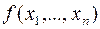 по всем переменным в виде
по всем переменным в виде
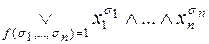
называется совершенной дизъюнктивной нормальной формой (СДНФ).
Пример 6.
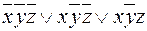 - СДНФ для функции
- СДНФ для функции 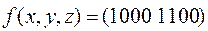 (см. пример 5).
(см. пример 5).
Теорема 2.
Всякая булева функция (кроме 0) имеет единственную СДНФ.
Доказательство. Согласно следствию из теоремы о разложении
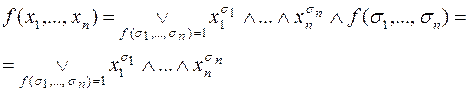
Замечание. Если под дизъюнкцией одного слагаемого понимать само это слагаемое, то дизъюнкции нуля слагаемых не существует, поэтому не существует СДНФ для функции 0.
При построении СДНФ имеет место следующее
Правило единицы. Рассматриваются только те наборы аргументов, на которых функция 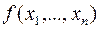 принимает значение 1; для каждого такого набора в СДНФ делается заготовка слагаемого
принимает значение 1; для каждого такого набора в СДНФ делается заготовка слагаемого 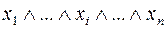 . Если в данном наборе аргументов
. Если в данном наборе аргументов 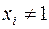 , то над переменной
, то над переменной 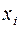 в заготовленном слагаемом навешивается отрицание:
в заготовленном слагаемом навешивается отрицание: 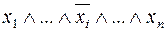 .
.
Теорема 3.
Всякая булева функция может быть выражена через дизъюнкцию, конъюнкцию и отрицание:
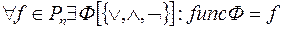 .
.
Доказательство.
Если 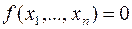 , то
, то 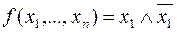 . Если
. Если 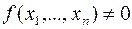 , то
, то
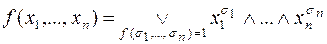 .
.
Теорема 4.
Всякая булева функция (кроме 1) может быть единственным образом выражена в виде совершенной конъюнктивной нормальной форме (СКНФ):
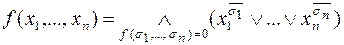 .
.
Доказательство.
Если 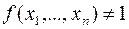 , то
, то 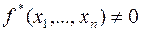 и
и
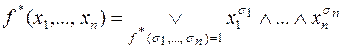 .
.
Применив к последнему тождеству принцип двойственности, находим
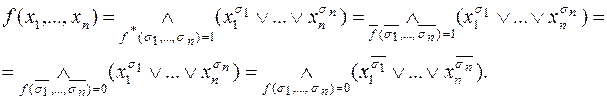
При построении СКНФ имеет место следующее
Правило нуля. Рассматриваются только те наборы аргументов, на которых функция 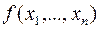 принимает значение 0; для каждого такого набора в СКНФ делается заготовка сомножителя
принимает значение 0; для каждого такого набора в СКНФ делается заготовка сомножителя 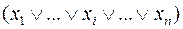 . Если в данном наборе аргументов
. Если в данном наборе аргументов 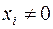 , то над переменной
, то над переменной 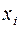 в заготовленном сомножителе навешивается отрицание:
в заготовленном сомножителе навешивается отрицание: 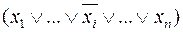 .
.
Пример 7.
Построим функцию для импликации: 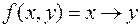 . Импликация принимает значение 0 на одном наборе:
. Импликация принимает значение 0 на одном наборе:
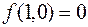 .
.
Так как в этом наборе 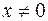 и
и 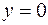 , то по правилу нуля получаем
, то по правилу нуля получаем
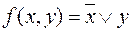 .
.
Итак, 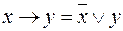 - искомая функция для импликации.
- искомая функция для импликации.
Полнота системы
Определение 4. Система функций {f1, f2, ..., fs, ...}ÌP2 называется полной в Р2, если любая функция f(x1, ..., xn) Î P2 может быть записана в виде формулы через функции этой системы.
Полные системы
1. P2 – полная система.
2. Система M={x1&x2, x1Úx2, 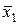 } – полная система, т.к. любая функция алгебры логики может быть записана в виде формулы через эти функции.
} – полная система, т.к. любая функция алгебры логики может быть записана в виде формулы через эти функции.
Пример 8. Неполные системы: { 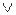 }, {0,1}.
}, {0,1}.
Лемма (достаточное условие полноты)
Пусть система  U = {f1, f2, ..., fs, ...} полна в Р2. Пусть B = {g1, g2, ..., gk, ...} – некоторая система из Р2, причем любая функция fi Î U может быть выражена формулой над B, тогда система B полна в Р2.
U = {f1, f2, ..., fs, ...} полна в Р2. Пусть B = {g1, g2, ..., gk, ...} – некоторая система из Р2, причем любая функция fi Î U может быть выражена формулой над B, тогда система B полна в Р2.
7. Система {x1&x2, x1Åx2, 0, 1} полна в Р2, U = {x1&x2, 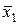 },
}, 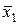 = x1Å1.
= x1Å1.
Полином Жегалкина
f(x1, ..., xn) Î P2, представим ее в виде формулы через конъюнкцию и сумму по модулю два, используя числа 0 и 1. Это можно сделать, так как {x1&x2, x1Åx2, 0, 1} полна в Р2. В силу свойства x & (yÅz) = xy Å xz можно раскрыть все скобки, привести подобные члены, и получится полином от n переменных, состоящий из членов вида х 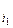 х
х 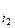 ...х
...х 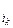 , соединенных знаком Å. Такой полином называется полиномом Жегалкина.
, соединенных знаком Å. Такой полином называется полиномом Жегалкина.
Общий вид полинома Жегалкина:
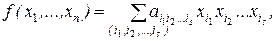
где 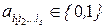 , s = 0, 1, ..., n, причем при s = 0 получаем свободный член а0.
, s = 0, 1, ..., n, причем при s = 0 получаем свободный член а0.
Представление функции в виде полинома Жегалкина
1. Представим любую функцию формулой над {x1&x2, 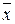 } и сделаем замену
} и сделаем замену 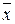 =xÅ1. Этот способ удобен, если функция задана формулой.
=xÅ1. Этот способ удобен, если функция задана формулой.
Пример 9. (x1 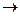 (x2
(x2 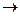 x3))(x1 Ú x2) x3 = (x1Ú x2 Ú x3)(x1 Ú x2) x3 = (`x1x2 Ú x1x3 Ú x1x2 Ú x2 Ú x2x3)x3 = (`x1x3 Ú x2)x3 = x1x3 x2 x3 = ((x1x3Å1)x2Å1)x3 = x1x2x3Åx2x3Åx3.
x3))(x1 Ú x2) x3 = (x1Ú x2 Ú x3)(x1 Ú x2) x3 = (`x1x2 Ú x1x3 Ú x1x2 Ú x2 Ú x2x3)x3 = (`x1x3 Ú x2)x3 = x1x3 x2 x3 = ((x1x3Å1)x2Å1)x3 = x1x2x3Åx2x3Åx3.
Надо помнить, что четное число одинаковых слагаемых в сумме по mod2 дает 0.
2. Метод неопределенных коэффициентов. Он удобен, если функция задана таблицей.
Пример 10.
Запишем с неопределенными коэффициентами полином Жегалкина для функции трех переменных f(x1, x2, x3) = (01101001) = а0 Å а1х1Å а2х2Å а3х3Å b1x1x2Å b2x2x3Åb3x1x3Åcx1x2x3. Затем находим коэффициенты, используя значения функции на всех наборах. На наборе (0, 0, 0) f(0, 0, 0) = 0, с другой стороны, подставив этот набор в полином, получим f(0, 0, 0) = а0, отсюда а0 = 0. f(0, 0, 1) = 1, подставив набор (0, 0, 1) в полином, получим: f(0, 0, 1) = а0 Å а3, т.к. а0 = 0, отсюда а3 = 1. Аналогично, f(0, 1, 0) = 1 = а2, f(0, 1, 1) = 0 = а2 Å а3 Å b2 b2 = 0; а1 = 1; 0 = а1 Å а3 Å b3 , b3 = 0; 0 = а1 Å а2 Å b1 , b1 = 0; 1 = 1 Å 1 Å 1 Å c; c = 0; тогда полином Жегалкина для данной функции примет вид: f(x1, x2, x3) = x1 Å x2 Å x3.
Многочлен Жегалкина можно получить также с помощью треугольника Паскаля по единицам его левой стороны по таблице следующим образом. Построим многочлен Жегалкина для функции f = (10011110). Верхняя сторона треугольника есть функция f. Любой другой элемент треугольника есть сумма по модулю для двух соседних элементов предыдущей строки. Левая сторона треугольника для функции f содержит шесть единиц. Многочлен Жегалкина будет содержать шесть слагаемых. Первая единица треугольника соответствует набору (000). Первое слагаемое многочлена есть 1. Третья снизу единица в левой стороне треугольника соответствует набору (101). В качестве слагаемого многочлена берем x1x3. Аналогично для других единиц треугольника. Слева от наборов показаны слагаемые многочлена Жегалкина.
| N | x1x2x3 | f | Треугольник Паскаля |
| x3 x2 x2x3 x1 x1x3 x1x2 x1x2x3 | 1 0 0 1 1 1 1 0 1 0 1 0 0 0 1 1 1 1 0 0 1 0 0 1 0 1 0 1 1 1 1 0 0 1 0 |
Тогда 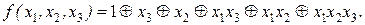
Теорема Жегалкина
Каждая функция из 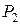 может быть представлена в виде полинома Жегалкина единственным образом.
может быть представлена в виде полинома Жегалкина единственным образом.
Здесь единственность понимается с точностью до порядка слагаемых в сумме и порядка сомножителей в конъюнкциях:
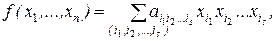
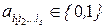 , s = 0, 1, ..., n.
, s = 0, 1, ..., n.
Доказательство.
Любая функция из Р2 может быть представлена формулой над {x1 & x2, x1Å x2, 0, 1}, а эта формула после раскрытия всех скобок и приведения подобных членов дает полином Жегалкина. Докажем единственность представления. Рассмотрим функции f(x1, ..., xn) от n переменных. Мы знаем, что всего таких функций, т.е. их таблиц истинности , 2n. Подсчитаем число различных полиномов Жегалкина от n переменных, т.е. число вариаций вида: 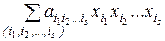 . Число наборов
. Число наборов 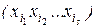 равно числу всех подмножеств множества { x1, ..., xn }, сюда входит и пустое множество (если s = 0). Число подмножеств множества из n элементов равно 2n , а так как каждый набор входит с коэффициентом
равно числу всех подмножеств множества { x1, ..., xn }, сюда входит и пустое множество (если s = 0). Число подмножеств множества из n элементов равно 2n , а так как каждый набор входит с коэффициентом 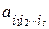 , принимающим два значения: 0 или 1, то число всевозможных полиномов будет
, принимающим два значения: 0 или 1, то число всевозможных полиномов будет 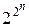 . Так как каждому полиному соответствует единственная функция, число функций от n переменных равно числу полиномов, то каждой функции будет соответствовать единственный полином.
. Так как каждому полиному соответствует единственная функция, число функций от n переменных равно числу полиномов, то каждой функции будет соответствовать единственный полином.
Определение.
Функция f(x1, ..., xn), полином Жегалкина для которой имеет следующий линейный относительно переменных вид: f = а0 Å а1х1 Å а2х2 Å ... Å аnхn, называется линейной.
Лемма о нелинейной функции.
Суперпозицией нелинейной функции, отрицания и константы 1 можно получить конъюнкцию.
Доказательство.
Пусть f(x1, ..., xn) – нелинейная функция. Тогда полином Жегалкина содержит для нее слагаемое, в котором присутствует произведение xixj. Будем считать для простоты, что x1x2 в многочлене Жегалкина является этим произведением. Произведя группировку слагаемых, функцию f представим в виде 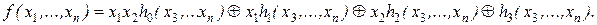
Функция h0 не есть тождественный нуль, иначе в полиноме Жегалкина отсутствует слагаемое с произведением x1x2. Тогда существует набор (a3, …, an) из 0 и 1, для которого h0(a3, …, an) = 1. Пусть h1(a3, …, an) = a, h2(a3, …, an) = b, h3(a3, …, an) = c. Тогда 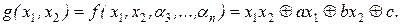
Построим функцию:
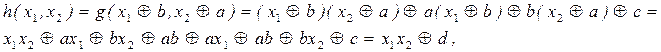 где d = ab Å c. Если d = 0, то h(x1, x2) = x1x2. Если d = 1, то h(x1, x2) = x1x2 Å 1 и тогда
где d = ab Å c. Если d = 0, то h(x1, x2) = x1x2. Если d = 1, то h(x1, x2) = x1x2 Å 1 и тогда 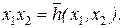 Лемма доказана.
Лемма доказана.
Функция f(x1, ..., xn) сохраняет константу a Î {0, 1}, если f(a, …, a) = a.
Пример 11.
Функция xy сохраняет 0, сохраняет 1. Функция x®y сохраняет 1 и не сохраняет 0.
Минимизация булевых функций
Минимизация нормальных форм
Минимальной ДНФ (МДНФ) функции f(x1, ... ,xn) называется ДНФ, реализующая функцию f и содержащая минимальное число символов переменных по сравнению со всеми другими видами ДНФ, реализующими функцию f.
Если для всякого набора 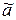 = (a1, ..., an) значений переменных условие g(
= (a1, ..., an) значений переменных условие g( 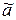 )=1 влечёт
)=1 влечёт 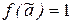 , то функция g называется частью функции f (или функция f накрывает функцию g). Если при этом для некоторого набора
, то функция g называется частью функции f (или функция f накрывает функцию g). Если при этом для некоторого набора 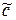 = (c1, ..., cn) функция g(
= (c1, ..., cn) функция g( 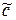 )=1, то говорят, что функция g накрывает единицу функции f на наборе
)=1, то говорят, что функция g накрывает единицу функции f на наборе 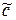 (или что g накрывает конституенту единицы
(или что g накрывает конституенту единицы 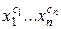 функции f). Заметим, что конституанта единицы функции f есть часть функции f, накрывающая единственную единицу функции f.
функции f). Заметим, что конституанта единицы функции f есть часть функции f, накрывающая единственную единицу функции f.
Элементарная конъюнкция K называется импликантом функции f, если для всякого набора 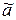 =(a1, ..., an) из 0 и 1 условие K(
=(a1, ..., an) из 0 и 1 условие K( 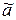 )=1 влечет f(
)=1 влечет f( 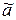 )=1.
)=1.
Импликант K функции f называется простым, если выражение, получающееся из него выбрасыванием любых множителей, уже не импликант функции f.
Ясно, что всякий импликант функции f есть часть функции f.
Теорема 5.
Всякая функция реализуется дизъюнкцией всех своих простых имликант (ПИ).
Доказательство.
Пусть f(x1, ..., xn) есть функция, а A = K1 v ... v Km – дизъюнкция всех ее простых импликант. Пусть 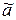 = (a1, ..., an) – произвольный набор длины n из 0 и 1.
= (a1, ..., an) – произвольный набор длины n из 0 и 1.
Если A( 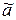 ) = 1, то найдется дизъюнктивное слагаемое Ki (
) = 1, то найдется дизъюнктивное слагаемое Ki ( 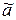 ) = 1, что влечет f(
) = 1, что влечет f( 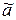 ) = 1, ибо Ki есть импликант функции f.
) = 1, ибо Ki есть импликант функции f.
Если f( 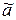 ) = 1, то в СДНФ для функции f найдется элементарная конъюнкция K, равная на этом наборе единице. Один из простых имликантов Kj функции f получается выбрасыванием некоторых множителей из K и потому Kj(
) = 1, то в СДНФ для функции f найдется элементарная конъюнкция K, равная на этом наборе единице. Один из простых имликантов Kj функции f получается выбрасыванием некоторых множителей из K и потому Kj( 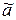 ) = 1, а тогда A(
) = 1, а тогда A( 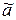 ) = 1.
) = 1.
Следовательно, f = A. Теорема доказана.
Сокращенная ДНФ функции f есть дизъюнкция всех простых импликант функции f. Всякая функция f реализуется своей сокращенной ДНФ. Для всякой функции, не равной тождественно нулю, существует единственная сокращенная ДНФ.
Пусть A и B – произвольные формулы. Из свойств булевых операций вытекают следующие обратимые правила преобразования ДНФ:
1) 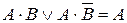 – полное склеивание (развертывание);
– полное склеивание (развертывание);
2) 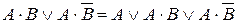 – неполное склеивание;
– неполное склеивание;
3) 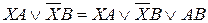 – обобщенное склеивание;
– обобщенное склеивание;
4)  – поглощение;
– поглощение;
5) 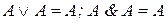 – идемпотентность ( удаление дублирующих членов).
– идемпотентность ( удаление дублирующих членов).
Теорема Квайна. Если в СДНФ функции f провести все операции неполного склеивания, а затем все операции поглощения и удаления дублирующих членов, то в результате получится сокращения ДНФ функции f.
Доказательство.
Пусть имеем сокращенную ДНФ функции f. Проведем все операции развертывания к каждому простому импликанту для получения недостающих переменных в каждом дизъюнктивном слагаемом сокращенной ДНФ. В полученном выражении из нескольких одинаковых дизъюнктивных слагаемых оставим только по одному экземпляру. В результате получим СДНФ функции f. Теперь, исходя из полученной СДНФ, в обратном порядке проведем операции добавления одинаковых дизъюнктивных слагаемых (с помощью правил идемпотентности), неполного склеивания и поглощения. В итоге получим исходную сокращенную ДНФ.
